Introduction

Procedurally generated animation of the anti-twister mechanism and its connection to Spin(3). Also known as Dirac's belt trick, a demonstration of an object that is subject to $4\pi$ or $720°$ symmetry, so it needs two full revolutions to revert to its initial state.

Inspired by Jason Hise's animations, please check out: https://en.wikipedia.org/wiki/User:JasonHise

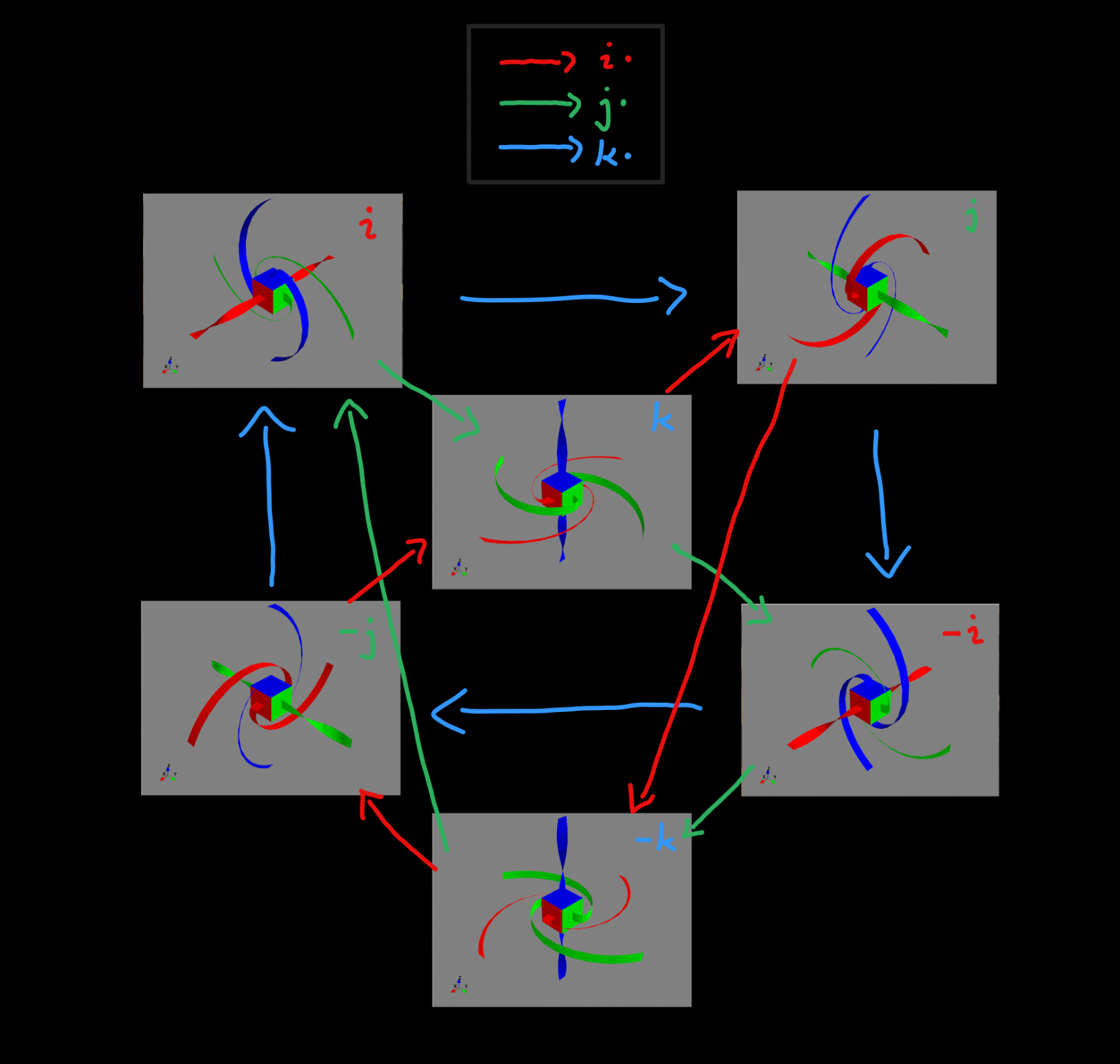States of the anti-twister and their corresponding spin observables as quaternions

How it works

Coded using CGA ($\mathrm{Cl}(4,1)$) motor interpolation as described by Belon et al (2017).

In order to model the ribbon that is secured in $\mathbf{s}$-direction while rotating in $\mathbf{r}$ by $2\pi \cdot \lambda \mathrm{rad}$. We define three oriented control points using CGA rotors. For this, using two rotors $R$ and $S$, describing the rotation of the center cube and the twisting of the ribbon $R(\lambda )=\exp (\frac{\mathbf{r}}{e_{123}}\pi \lambda ),$ $S=\exp (-\frac{\mathbf{s}}{e_{123}}\frac{\pi }{2})$ and three translators $T_0(\lambda )=1-\frac{R(\lambda )0.3\mathbf{s}R(\lambda {)}^{†}\wedge e_{\mathrm{\infty }}}{2},$ $T_1(\lambda )=1-\frac{R(\lambda )1.0\mathbf{s}R(\lambda {)}^{†}\wedge e_{\mathrm{\infty }}}{2},$ $T_2=1-\frac{2.0\mathbf{s}\wedge e_{\mathrm{\infty }}}{2}$ we define the motors of oriented control points as $M_0(\lambda )=T_0(\lambda )R(\lambda )S$ $M_1(\lambda )=T_1(\lambda )R(\lambda )S$ $M_2(\lambda )=T_2$ Which can be interpolated linearly using motor logarithms: $M(\lambda ,\alpha )=\exp (\sum _i{B}_i(\alpha )\log (M_i(\lambda )))$ Where $\alpha \in [0,1]$ is the interpolation parameter along the ribbon originating from the center cube face. And $B_i(\alpha )$ are weight functions defined using $B_i(\alpha )=B_i^{\prime }(\alpha )/\sum _j{B}_j^{\prime }(\alpha )$ which is normalizing $B_1^{\prime }(\alpha )=(1-\alpha {)}^2,$ $B_2^{\prime }(\alpha )=10{\alpha }^2(1-\alpha {)}^4,$ $B_3^{\prime }(\alpha )={\alpha }^3$.

Finally, the interpolation motor $M(\lambda ,\alpha )$ can be used to calculate the mesh of a ribbon extending in $\mathbf{c}$ direction ${\rho }_{l,r}(\lambda ,\alpha )=M(\lambda ,\alpha )(\pm \uparrow \mathbf{c})M(\lambda ,\alpha {)}^{†}.$ Where ${\rho }_l(\lambda ,\alpha )$ and ${\rho }_r(\lambda ,\alpha )$ are its left and right boundaries respectively and we used the up-projection $\uparrow \mathbf{c}$ for the conformal representation defined by $\uparrow \mathbf{c}=\mathbf{c}+\frac{1}{2}{\mathbf{c}}^2{e}_{\mathrm{\infty }}+e_o$.

The full set of twelve equations (2 boundaries $\times$ 6 directions) for rotating in the $z$-axis is given by

$${\rho }_{l,r}^{+x}(\lambda ,\alpha )=\underset{―}{M(\lambda ,\alpha ,\mathbf{s}=+e_1,\mathbf{r}=e_3)}(\uparrow \pm 0.1e_2)$$ $${\rho }_{l,r}^{-x}(\lambda ,\alpha )=\underset{―}{M(\lambda +1,\alpha ,\mathbf{s}=-e_1,\mathbf{r}=e_3)}(\uparrow \pm 0.1e_2)$$ $${\rho }_{l,r}^{+y}(\lambda ,\alpha )=\underset{―}{M(\lambda +\frac{3}{2},\alpha ,\mathbf{s}=+e_2,\mathbf{r}=e_3)}(\uparrow \pm 0.1e_3)$$ $${\rho }_{l,r}^{-y}(\lambda ,\alpha )=\underset{―}{M(\lambda +\frac{1}{2},\alpha ,\mathbf{s}=-e_2,\mathbf{r}=e_3)}(\uparrow \pm 0.1e_3)$$ $${\rho }_{l,r}^{+z}(\lambda ,\alpha )=\underset{―}{R_{12}(\frac{\lambda }{2})M(\frac{1}{2},\alpha ,\mathbf{s}=+e_3,\mathbf{r}=e_2))R_{12}(-\frac{\lambda }{2})}(\uparrow \pm 0.1e_1)$$ $${\rho }_{l,r}^{-z}(\lambda ,\alpha )=\underset{―}{R_{12}(\frac{\lambda }{2})M(\frac{3}{2},\alpha ,\mathbf{s}=-e_3,\mathbf{r}=e_2))R_{12}(-\frac{\lambda }{2})}(\uparrow \pm 0.1e_1).$$

Where we used $\underset{―}{M}(x)$ to denote the sandwich-product $Mx{M}^{†}$ of $x$. The ${\rho }_{l,r}^{\pm i}(\lambda ,\alpha )$ are at last projected back into $\mathrm{Cl}(3,0)$ by using

$$\downarrow \rho =(\frac{\rho }{\rho \cdot e_{\mathrm{\infty }}}\wedge e_{+}\wedge e_{-})(e_{+}\wedge e_{-}{)}^{-1}$$

Which first normalizes the conformal point by dividing it with $\rho \cdot e_{\mathrm{\infty }}$ and then rejects it from the Minkowski plane $e_{+}\wedge e_{-}$.

How to it compile yourself

After cd in the project folder download dependencies using

pip install -r requirements.txt

After that, you may use pyinstaller to build an executable

pyinstaller ./Spinor_Cube_Ver2.2.2.py --onefile

References:

[1] Belon, M.C.L., Hildenbrand, D. Practical Geometric Modeling Using Geometric Algebra Motors. Adv. Appl. Clifford Algebras 27, 2019–2033 (2017). https://doi.org/10.1007/s00006-017-0777-z