diff --git a/Assets/Origins/Categories-List.md b/Assets/Origins/Categories-List.md
index 62282f69..69991c95 100644
--- a/Assets/Origins/Categories-List.md
+++ b/Assets/Origins/Categories-List.md
@@ -235,7 +235,7 @@
### [枚举算法题目](../../Contents/09.Algorithm-Base/01.Enumeration-Algorithm/02.Enumeration-Algorithm-List.md)
-###### 0001. 两数之和、0204. 计数质数、1925. 统计平方和三元组的数目、1450. 在既定时间做作业的学生人数、1620. 网络信号最好的坐标、剑指 Offer 57 - II. 和为s的连续正数序列、0078. 子集、0090. 子集 II、0800. 相似 RGB 颜色、0221. 最大正方形、0560. 和为 K 的子数组
+###### 0001. 两数之和、0204. 计数质数、1925. 统计平方和三元组的数目、1450. 在既定时间做作业的学生人数、1620. 网络信号最好的坐标、剑指 Offer 57 - II. 和为s的连续正数序列、0800. 相似 RGB 颜色、0221. 最大正方形、0560. 和为 K 的子数组
### [递归算法题目](../../Contents/09.Algorithm-Base/02.Recursive-Algorithm/02.Recursive-Algorithm-List.md)
@@ -255,7 +255,7 @@
### [位运算题目](../../Contents/09.Algorithm-Base/06.Bit-Operation/02.Bit-Operation-List.md)
-###### 0504. 七进制数、0405. 数字转换为十六进制数、0190. 颠倒二进制位、1009. 十进制整数的反码、0191. 位1的个数、0371. 两整数之和、0089. 格雷编码、0201. 数字范围按位与、0338. 比特位计数、0136. 只出现一次的数字、0137. 只出现一次的数字 II、0260. 只出现一次的数字 III、0268. 丢失的数字、1349. 参加考试的最大学生数、0645. 错误的集合
+###### 0504. 七进制数、0405. 数字转换为十六进制数、0190. 颠倒二进制位、1009. 十进制整数的反码、0191. 位1的个数、0371. 两整数之和、0089. 格雷编码、0201. 数字范围按位与、0338. 比特位计数、0136. 只出现一次的数字、0137. 只出现一次的数字 II、0260. 只出现一次的数字 III、0268. 丢失的数字、1349. 参加考试的最大学生数、0645. 错误的集合、0078. 子集、0090. 子集 II
## 10. 动态规划
diff --git a/Contents/00.Introduction/04.Solutions-List.md b/Contents/00.Introduction/04.Solutions-List.md
index 78203a43..84be48d3 100644
--- a/Contents/00.Introduction/04.Solutions-List.md
+++ b/Contents/00.Introduction/04.Solutions-List.md
@@ -1,4 +1,4 @@
-# LeetCode 题解(已完成 742 道)
+# LeetCode 题解(已完成 746 道)
| 题号 | 标题 | 题解 | 标签 | 难度 |
| :------ | :------ | :------ | :------ | :------ |
@@ -60,6 +60,7 @@
| 0061 | [旋转链表](https://leetcode.cn/problems/rotate-list/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0061.%20%E6%97%8B%E8%BD%AC%E9%93%BE%E8%A1%A8.md) | 链表、双指针 | 中等 |
| 0062 | [不同路径](https://leetcode.cn/problems/unique-paths/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0062.%20%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84.md) | 数组、动态规划 | 中等 |
| 0063 | [不同路径 II](https://leetcode.cn/problems/unique-paths-ii/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0063.%20%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84%20II.md) | 数组、动态规划、矩阵 | 中等 |
+| 0064 | [最小路径和](https://leetcode.cn/problems/minimum-path-sum/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0064.%20%E6%9C%80%E5%B0%8F%E8%B7%AF%E5%BE%84%E5%92%8C.md) | | 简单 |
| 0066 | [加一](https://leetcode.cn/problems/plus-one/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0066.%20%E5%8A%A0%E4%B8%80.md) | 数组 | 简单 |
| 0067 | [二进制求和](https://leetcode.cn/problems/add-binary/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0067.%20%E4%BA%8C%E8%BF%9B%E5%88%B6%E6%B1%82%E5%92%8C.md) | 数学、字符串、位运算 | 简单 |
| 0069 | [x 的平方根](https://leetcode.cn/problems/sqrtx/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0069.%20x%20%E7%9A%84%E5%B9%B3%E6%96%B9%E6%A0%B9.md) | 数学、二分查找 | 简单 |
@@ -161,7 +162,7 @@
| 0201 | [数字范围按位与](https://leetcode.cn/problems/bitwise-and-of-numbers-range/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0201.%20%E6%95%B0%E5%AD%97%E8%8C%83%E5%9B%B4%E6%8C%89%E4%BD%8D%E4%B8%8E.md) | 位运算 | 中等 |
| 0202 | [快乐数](https://leetcode.cn/problems/happy-number/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0202.%20%E5%BF%AB%E4%B9%90%E6%95%B0.md) | 哈希表、数学 | 简单 |
| 0203 | [移除链表元素](https://leetcode.cn/problems/remove-linked-list-elements/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0203.%20%E7%A7%BB%E9%99%A4%E9%93%BE%E8%A1%A8%E5%85%83%E7%B4%A0.md) | 链表 | 简单 |
-| 0204 | [计数质数](https://leetcode.cn/problems/count-primes/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0204.%20%E8%AE%A1%E6%95%B0%E8%B4%A8%E6%95%B0.md) | 数学、哈希表 | 简单 |
+| 0204 | [计数质数](https://leetcode.cn/problems/count-primes/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0204.%20%E8%AE%A1%E6%95%B0%E8%B4%A8%E6%95%B0.md) | 数组、数学、枚举、数论 | 简单 |
| 0205 | [同构字符串](https://leetcode.cn/problems/isomorphic-strings/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0205.%20%E5%90%8C%E6%9E%84%E5%AD%97%E7%AC%A6%E4%B8%B2.md) | 哈希表 | 简单 |
| 0206 | [反转链表](https://leetcode.cn/problems/reverse-linked-list/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0206.%20%E5%8F%8D%E8%BD%AC%E9%93%BE%E8%A1%A8.md) | 链表 | 简单 |
| 0207 | [课程表](https://leetcode.cn/problems/course-schedule/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0207.%20%E8%AF%BE%E7%A8%8B%E8%A1%A8.md) | 深度优先搜索、广度优先搜索、图、拓扑排序 | 中等 |
@@ -295,6 +296,7 @@
| 0461 | [汉明距离](https://leetcode.cn/problems/hamming-distance/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0461.%20%E6%B1%89%E6%98%8E%E8%B7%9D%E7%A6%BB.md) | 位运算 | 简单 |
| 0463 | [岛屿的周长](https://leetcode.cn/problems/island-perimeter/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0463.%20%E5%B2%9B%E5%B1%BF%E7%9A%84%E5%91%A8%E9%95%BF.md) | 深度优先搜索、广度优先搜索、数组、矩阵 | 中等 |
| 0467 | [环绕字符串中唯一的子字符串](https://leetcode.cn/problems/unique-substrings-in-wraparound-string/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0467.%20%E7%8E%AF%E7%BB%95%E5%AD%97%E7%AC%A6%E4%B8%B2%E4%B8%AD%E5%94%AF%E4%B8%80%E7%9A%84%E5%AD%90%E5%AD%97%E7%AC%A6%E4%B8%B2.md) | 字符串、动态规划 | 中等 |
+| 0468 | [验证IP地址](https://leetcode.cn/problems/validate-ip-address/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0468.%20%E9%AA%8C%E8%AF%81IP%E5%9C%B0%E5%9D%80.md) | 字符串 | 中等 |
| 0473 | [火柴拼正方形](https://leetcode.cn/problems/matchsticks-to-square/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0473.%20%E7%81%AB%E6%9F%B4%E6%8B%BC%E6%AD%A3%E6%96%B9%E5%BD%A2.md) | 位运算、数组、动态规划、回溯、状态压缩 | 中等 |
| 0474 | [一和零](https://leetcode.cn/problems/ones-and-zeroes/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0474.%20%E4%B8%80%E5%92%8C%E9%9B%B6.md) | 数组、字符串、动态规划 | 中等 |
| 0480 | [滑动窗口中位数](https://leetcode.cn/problems/sliding-window-median/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0480.%20%E6%BB%91%E5%8A%A8%E7%AA%97%E5%8F%A3%E4%B8%AD%E4%BD%8D%E6%95%B0.md) | 数组、哈希表、滑动窗口、堆(优先队列) | 困难 |
@@ -544,7 +546,9 @@
| 2023 | [连接后等于目标字符串的字符串对](https://leetcode.cn/problems/number-of-pairs-of-strings-with-concatenation-equal-to-target/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/2023.%20%E8%BF%9E%E6%8E%A5%E5%90%8E%E7%AD%89%E4%BA%8E%E7%9B%AE%E6%A0%87%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E5%AD%97%E7%AC%A6%E4%B8%B2%E5%AF%B9.md) | 数组、字符串 | 中等 |
| 2156 | [查找给定哈希值的子串](https://leetcode.cn/problems/find-substring-with-given-hash-value/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/2156.%20%E6%9F%A5%E6%89%BE%E7%BB%99%E5%AE%9A%E5%93%88%E5%B8%8C%E5%80%BC%E7%9A%84%E5%AD%90%E4%B8%B2.md) | 字符串、滑动窗口、哈希函数、滚动哈希 | 中等 |
| 2235 | [两整数相加](https://leetcode.cn/problems/add-two-integers/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/2235.%20%E4%B8%A4%E6%95%B4%E6%95%B0%E7%9B%B8%E5%8A%A0.md) | 数学 | 简单 |
+| 2249 | [统计圆内格点数目](https://leetcode.cn/problems/count-lattice-points-inside-a-circle/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/2249.%20%E7%BB%9F%E8%AE%A1%E5%9C%86%E5%86%85%E6%A0%BC%E7%82%B9%E6%95%B0%E7%9B%AE.md) | 几何、数组、哈希表、数学、枚举 | 中等 |
| 2276 | [统计区间中的整数数目](https://leetcode.cn/problems/count-integers-in-intervals/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/2276.%20%E7%BB%9F%E8%AE%A1%E5%8C%BA%E9%97%B4%E4%B8%AD%E7%9A%84%E6%95%B4%E6%95%B0%E6%95%B0%E7%9B%AE.md) | 设计、线段树、有序集合 | 困难 |
+| 2427 | [公因子的数目](https://leetcode.cn/problems/number-of-common-factors/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/2427.%20%E5%85%AC%E5%9B%A0%E5%AD%90%E7%9A%84%E6%95%B0%E7%9B%AE.md) | 数学、枚举、数论 | 简单 |
| 剑指 Offer 03 | [数组中重复的数字](https://leetcode.cn/problems/shu-zu-zhong-zhong-fu-de-shu-zi-lcof/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/%E5%89%91%E6%8C%87%20Offer%2003.%20%E6%95%B0%E7%BB%84%E4%B8%AD%E9%87%8D%E5%A4%8D%E7%9A%84%E6%95%B0%E5%AD%97.md) | 数组、哈希表、排序 | 简单 |
| 剑指 Offer 04 | [二维数组中的查找](https://leetcode.cn/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/%E5%89%91%E6%8C%87%20Offer%2004.%20%E4%BA%8C%E7%BB%B4%E6%95%B0%E7%BB%84%E4%B8%AD%E7%9A%84%E6%9F%A5%E6%89%BE.md) | 数组、二分查找、分治、矩阵 | 中等 |
| 剑指 Offer 05 | [替换空格](https://leetcode.cn/problems/ti-huan-kong-ge-lcof/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/%E5%89%91%E6%8C%87%20Offer%2005.%20%E6%9B%BF%E6%8D%A2%E7%A9%BA%E6%A0%BC.md) | 字符串 | 简单 |
diff --git a/Contents/00.Introduction/05.Categories-List.md b/Contents/00.Introduction/05.Categories-List.md
index 08e1d7ca..0c31edb9 100644
--- a/Contents/00.Introduction/05.Categories-List.md
+++ b/Contents/00.Introduction/05.Categories-List.md
@@ -704,13 +704,11 @@
| 题号 | 标题 | 题解 | 标签 | 难度 |
| :------ | :------ | :------ | :------ | :------ |
| 0001 | [两数之和](https://leetcode.cn/problems/two-sum/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0001.%20%E4%B8%A4%E6%95%B0%E4%B9%8B%E5%92%8C.md) | 数组、哈希表 | 简单 |
-| 0204 | [计数质数](https://leetcode.cn/problems/count-primes/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0204.%20%E8%AE%A1%E6%95%B0%E8%B4%A8%E6%95%B0.md) | 数学、哈希表 | 简单 |
+| 0204 | [计数质数](https://leetcode.cn/problems/count-primes/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0204.%20%E8%AE%A1%E6%95%B0%E8%B4%A8%E6%95%B0.md) | 数组、数学、枚举、数论 | 简单 |
| 1925 | [统计平方和三元组的数目](https://leetcode.cn/problems/count-square-sum-triples/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1925.%20%E7%BB%9F%E8%AE%A1%E5%B9%B3%E6%96%B9%E5%92%8C%E4%B8%89%E5%85%83%E7%BB%84%E7%9A%84%E6%95%B0%E7%9B%AE.md) | 数学、枚举 | 简单 |
| 1450 | [在既定时间做作业的学生人数](https://leetcode.cn/problems/number-of-students-doing-homework-at-a-given-time/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1450.%20%E5%9C%A8%E6%97%A2%E5%AE%9A%E6%97%B6%E9%97%B4%E5%81%9A%E4%BD%9C%E4%B8%9A%E7%9A%84%E5%AD%A6%E7%94%9F%E4%BA%BA%E6%95%B0.md) | 数组 | 简单 |
| 1620 | 网络信号最好的坐标 | | | |
| 剑指 Offer 57 - II | [和为s的连续正数序列](https://leetcode.cn/problems/he-wei-sde-lian-xu-zheng-shu-xu-lie-lcof/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/%E5%89%91%E6%8C%87%20Offer%2057%20-%20II.%20%E5%92%8C%E4%B8%BAs%E7%9A%84%E8%BF%9E%E7%BB%AD%E6%AD%A3%E6%95%B0%E5%BA%8F%E5%88%97.md) | 数学、双指针、枚举 | 简单 |
-| 0078 | [子集](https://leetcode.cn/problems/subsets/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0078.%20%E5%AD%90%E9%9B%86.md) | 位运算、数组、回溯算法 | 中等 |
-| 0090 | [子集 II](https://leetcode.cn/problems/subsets-ii/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0090.%20%E5%AD%90%E9%9B%86%20II.md) | 位运算、数组、回溯 | 中等 |
| 0800 | [相似 RGB 颜色](https://leetcode.cn/problems/similar-rgb-color/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0800.%20%E7%9B%B8%E4%BC%BC%20RGB%20%E9%A2%9C%E8%89%B2.md) | 数学、字符串、枚举 | 简单 |
| 0221 | [最大正方形](https://leetcode.cn/problems/maximal-square/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0221.%20%E6%9C%80%E5%A4%A7%E6%AD%A3%E6%96%B9%E5%BD%A2.md) | 数组、动态规划、矩阵 | 中等 |
| 0560 | [和为 K 的子数组](https://leetcode.cn/problems/subarray-sum-equals-k/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0560.%20%E5%92%8C%E4%B8%BA%20K%20%E7%9A%84%E5%AD%90%E6%95%B0%E7%BB%84.md) | 数组、哈希表、前缀和 | 中等 |
@@ -819,6 +817,8 @@
| 0268 | [丢失的数字](https://leetcode.cn/problems/missing-number/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0268.%20%E4%B8%A2%E5%A4%B1%E7%9A%84%E6%95%B0%E5%AD%97.md) | 位运算、数组、数学 | 简单 |
| 1349 | 参加考试的最大学生数 | | | |
| 0645 | 错误的集合 | | | |
+| 0078 | [子集](https://leetcode.cn/problems/subsets/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0078.%20%E5%AD%90%E9%9B%86.md) | 位运算、数组、回溯算法 | 中等 |
+| 0090 | [子集 II](https://leetcode.cn/problems/subsets-ii/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0090.%20%E5%AD%90%E9%9B%86%20II.md) | 位运算、数组、回溯 | 中等 |
## 10. 动态规划
diff --git a/Contents/00.Introduction/06.Interview-100-List.md b/Contents/00.Introduction/06.Interview-100-List.md
index 79408bb5..3ac29955 100644
--- a/Contents/00.Introduction/06.Interview-100-List.md
+++ b/Contents/00.Introduction/06.Interview-100-List.md
@@ -345,7 +345,7 @@
| 0300 | [最长递增子序列](https://leetcode.cn/problems/longest-increasing-subsequence/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0300.%20%E6%9C%80%E9%95%BF%E9%80%92%E5%A2%9E%E5%AD%90%E5%BA%8F%E5%88%97.md) | 二分查找、动态规划 | 中等 |
| 1143 | [最长公共子序列](https://leetcode.cn/problems/longest-common-subsequence/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1143.%20%E6%9C%80%E9%95%BF%E5%85%AC%E5%85%B1%E5%AD%90%E5%BA%8F%E5%88%97.md) | 字符串、动态规划 | 中等 |
| 0718 | [最长重复子数组](https://leetcode.cn/problems/maximum-length-of-repeated-subarray/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0718.%20%E6%9C%80%E9%95%BF%E9%87%8D%E5%A4%8D%E5%AD%90%E6%95%B0%E7%BB%84.md) | 数组、二分查找、动态规划、滑动窗口、哈希函数、滚动哈希 | 中等 |
-| 0064 | 最小路径和 | | | |
+| 0064 | [最小路径和](https://leetcode.cn/problems/minimum-path-sum/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0064.%20%E6%9C%80%E5%B0%8F%E8%B7%AF%E5%BE%84%E5%92%8C.md) | | 简单 |
| 0072 | [编辑距离](https://leetcode.cn/problems/edit-distance/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0072.%20%E7%BC%96%E8%BE%91%E8%B7%9D%E7%A6%BB.md) | 字符串、动态规划 | 困难 |
| 0032 | [最长有效括号](https://leetcode.cn/problems/longest-valid-parentheses/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0032.%20%E6%9C%80%E9%95%BF%E6%9C%89%E6%95%88%E6%8B%AC%E5%8F%B7.md) | 栈、字符串、动态规划 | 困难 |
| 0221 | [最大正方形](https://leetcode.cn/problems/maximal-square/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0221.%20%E6%9C%80%E5%A4%A7%E6%AD%A3%E6%96%B9%E5%BD%A2.md) | 数组、动态规划、矩阵 | 中等 |
@@ -367,7 +367,7 @@
| :------ | :------ | :------ | :------ | :------ |
| 0008 | [字符串转换整数 (atoi)](https://leetcode.cn/problems/string-to-integer-atoi/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0008.%20%E5%AD%97%E7%AC%A6%E4%B8%B2%E8%BD%AC%E6%8D%A2%E6%95%B4%E6%95%B0%20%28atoi%29.md) | 数学、字符串 | 中等 |
| 0165 | 比较版本号 | | | |
-| 0468 | 验证IP地址 | | | |
+| 0468 | [验证IP地址](https://leetcode.cn/problems/validate-ip-address/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0468.%20%E9%AA%8C%E8%AF%81IP%E5%9C%B0%E5%9D%80.md) | 字符串 | 中等 |
#### 思维锻炼题目
diff --git a/Contents/00.Introduction/07.Interview-200-List.md b/Contents/00.Introduction/07.Interview-200-List.md
index 445c9150..4ce36ca4 100644
--- a/Contents/00.Introduction/07.Interview-200-List.md
+++ b/Contents/00.Introduction/07.Interview-200-List.md
@@ -476,7 +476,7 @@
| 0300 | [最长递增子序列](https://leetcode.cn/problems/longest-increasing-subsequence/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0300.%20%E6%9C%80%E9%95%BF%E9%80%92%E5%A2%9E%E5%AD%90%E5%BA%8F%E5%88%97.md) | 二分查找、动态规划 | 中等 |
| 1143 | [最长公共子序列](https://leetcode.cn/problems/longest-common-subsequence/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1143.%20%E6%9C%80%E9%95%BF%E5%85%AC%E5%85%B1%E5%AD%90%E5%BA%8F%E5%88%97.md) | 字符串、动态规划 | 中等 |
| 0718 | [最长重复子数组](https://leetcode.cn/problems/maximum-length-of-repeated-subarray/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0718.%20%E6%9C%80%E9%95%BF%E9%87%8D%E5%A4%8D%E5%AD%90%E6%95%B0%E7%BB%84.md) | 数组、二分查找、动态规划、滑动窗口、哈希函数、滚动哈希 | 中等 |
-| 0064 | 最小路径和 | | | |
+| 0064 | [最小路径和](https://leetcode.cn/problems/minimum-path-sum/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0064.%20%E6%9C%80%E5%B0%8F%E8%B7%AF%E5%BE%84%E5%92%8C.md) | | 简单 |
| 0072 | [编辑距离](https://leetcode.cn/problems/edit-distance/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0072.%20%E7%BC%96%E8%BE%91%E8%B7%9D%E7%A6%BB.md) | 字符串、动态规划 | 困难 |
| 0032 | [最长有效括号](https://leetcode.cn/problems/longest-valid-parentheses/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0032.%20%E6%9C%80%E9%95%BF%E6%9C%89%E6%95%88%E6%8B%AC%E5%8F%B7.md) | 栈、字符串、动态规划 | 困难 |
| 0221 | [最大正方形](https://leetcode.cn/problems/maximal-square/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0221.%20%E6%9C%80%E5%A4%A7%E6%AD%A3%E6%96%B9%E5%BD%A2.md) | 数组、动态规划、矩阵 | 中等 |
@@ -529,7 +529,7 @@
| :------ | :------ | :------ | :------ | :------ |
| 0008 | [字符串转换整数 (atoi)](https://leetcode.cn/problems/string-to-integer-atoi/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0008.%20%E5%AD%97%E7%AC%A6%E4%B8%B2%E8%BD%AC%E6%8D%A2%E6%95%B4%E6%95%B0%20%28atoi%29.md) | 数学、字符串 | 中等 |
| 0165 | 比较版本号 | | | |
-| 0468 | 验证IP地址 | | | |
+| 0468 | [验证IP地址](https://leetcode.cn/problems/validate-ip-address/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0468.%20%E9%AA%8C%E8%AF%81IP%E5%9C%B0%E5%9D%80.md) | 字符串 | 中等 |
| 0086 | 分隔链表 | | | |
#### 前缀和
diff --git a/Contents/09.Algorithm-Base/01.Enumeration-Algorithm/02.Enumeration-Algorithm-List.md b/Contents/09.Algorithm-Base/01.Enumeration-Algorithm/02.Enumeration-Algorithm-List.md
index 9d62b0b5..9aee54d6 100644
--- a/Contents/09.Algorithm-Base/01.Enumeration-Algorithm/02.Enumeration-Algorithm-List.md
+++ b/Contents/09.Algorithm-Base/01.Enumeration-Algorithm/02.Enumeration-Algorithm-List.md
@@ -3,13 +3,11 @@
| 题号 | 标题 | 题解 | 标签 | 难度 |
| :------ | :------ | :------ | :------ | :------ |
| 0001 | [两数之和](https://leetcode.cn/problems/two-sum/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0001.%20%E4%B8%A4%E6%95%B0%E4%B9%8B%E5%92%8C.md) | 数组、哈希表 | 简单 |
-| 0204 | [计数质数](https://leetcode.cn/problems/count-primes/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0204.%20%E8%AE%A1%E6%95%B0%E8%B4%A8%E6%95%B0.md) | 数学、哈希表 | 简单 |
+| 0204 | [计数质数](https://leetcode.cn/problems/count-primes/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0204.%20%E8%AE%A1%E6%95%B0%E8%B4%A8%E6%95%B0.md) | 数组、数学、枚举、数论 | 简单 |
| 1925 | [统计平方和三元组的数目](https://leetcode.cn/problems/count-square-sum-triples/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1925.%20%E7%BB%9F%E8%AE%A1%E5%B9%B3%E6%96%B9%E5%92%8C%E4%B8%89%E5%85%83%E7%BB%84%E7%9A%84%E6%95%B0%E7%9B%AE.md) | 数学、枚举 | 简单 |
| 1450 | [在既定时间做作业的学生人数](https://leetcode.cn/problems/number-of-students-doing-homework-at-a-given-time/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1450.%20%E5%9C%A8%E6%97%A2%E5%AE%9A%E6%97%B6%E9%97%B4%E5%81%9A%E4%BD%9C%E4%B8%9A%E7%9A%84%E5%AD%A6%E7%94%9F%E4%BA%BA%E6%95%B0.md) | 数组 | 简单 |
| 1620 | 网络信号最好的坐标 | | | |
| 剑指 Offer 57 - II | [和为s的连续正数序列](https://leetcode.cn/problems/he-wei-sde-lian-xu-zheng-shu-xu-lie-lcof/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/%E5%89%91%E6%8C%87%20Offer%2057%20-%20II.%20%E5%92%8C%E4%B8%BAs%E7%9A%84%E8%BF%9E%E7%BB%AD%E6%AD%A3%E6%95%B0%E5%BA%8F%E5%88%97.md) | 数学、双指针、枚举 | 简单 |
-| 0078 | [子集](https://leetcode.cn/problems/subsets/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0078.%20%E5%AD%90%E9%9B%86.md) | 位运算、数组、回溯算法 | 中等 |
-| 0090 | [子集 II](https://leetcode.cn/problems/subsets-ii/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0090.%20%E5%AD%90%E9%9B%86%20II.md) | 位运算、数组、回溯 | 中等 |
| 0800 | [相似 RGB 颜色](https://leetcode.cn/problems/similar-rgb-color/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0800.%20%E7%9B%B8%E4%BC%BC%20RGB%20%E9%A2%9C%E8%89%B2.md) | 数学、字符串、枚举 | 简单 |
| 0221 | [最大正方形](https://leetcode.cn/problems/maximal-square/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0221.%20%E6%9C%80%E5%A4%A7%E6%AD%A3%E6%96%B9%E5%BD%A2.md) | 数组、动态规划、矩阵 | 中等 |
| 0560 | [和为 K 的子数组](https://leetcode.cn/problems/subarray-sum-equals-k/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0560.%20%E5%92%8C%E4%B8%BA%20K%20%E7%9A%84%E5%AD%90%E6%95%B0%E7%BB%84.md) | 数组、哈希表、前缀和 | 中等 |
diff --git a/Contents/09.Algorithm-Base/04.Backtracking-Algorithm/01.Backtracking-Algorithm.md b/Contents/09.Algorithm-Base/04.Backtracking-Algorithm/01.Backtracking-Algorithm.md
index 8c74e550..af90c8df 100644
--- a/Contents/09.Algorithm-Base/04.Backtracking-Algorithm/01.Backtracking-Algorithm.md
+++ b/Contents/09.Algorithm-Base/04.Backtracking-Algorithm/01.Backtracking-Algorithm.md
@@ -169,17 +169,34 @@ for i in range(len(nums)): # 枚举可选元素列表
**描述**:给定一个整数数组 `nums`,数组中的元素互不相同。
-**要求**:返回该数组所有可能的不重复子集。
+**要求**:返回该数组所有可能的不重复子集。可以按任意顺序返回解集。
+
+**说明**:
+
+- $1 \le nums.length \le 10$。
+- $-10 \le nums[i] \le 10$。
+- `nums` 中的所有元素互不相同。
**示例**:
+- 示例 1:
+
+```Python
+输入 nums = [1,2,3]
+输出 [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
+```
+
+- 示例 2:
+
```Python
-输入 nums = [1,2,3]
-输出 [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
+输入:nums = [0]
+输出:[[],[0]]
```
#### 5.1.3 解题思路
+##### 思路 1:回溯算法
+
数组的每个元素都有两个选择:选与不选。
我们可以通过向当前子集数组中添加可选元素来表示选择该元素。也可以在当前递归结束之后,将之前添加的元素从当前子集数组中移除(也就是回溯)来表示不选择该元素。
@@ -216,7 +233,7 @@ for i in range(len(nums)): # 枚举可选元素列表
- 当遍历到决策树的叶子节点时,就终止了。也就是当正在考虑的元素位置到达数组末尾(即 `start >= len(nums)`)时,递归停止。
- 从决策树中也可以看出,子集需要存储的答案集合应该包含决策树上所有的节点,应该需要保存递归搜索的所有状态。所以无论是否达到终止条件,我们都应该将当前符合条件的结果放入到集合中。
-#### 5.1.4 代码
+##### 思路 1:代码
```Python
class Solution:
@@ -237,6 +254,11 @@ class Solution:
return res
```
+##### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(n \times 2^n)$,其中 $n$ 指的是数组 `nums` 的元素个数,$2^n$ 指的是所有状态数。每种状态需要 $O(n)$ 的时间来构造子集。
+- **空间复杂度**:$O(n)$,每种状态下构造子集需要使用 $O(n)$ 的空间。
+
### 5.2 N 皇后
#### 5.2.1 题目链接
@@ -257,16 +279,20 @@ class Solution:
**示例**:
+- 示例 1:
+
```Python
-输入 n = 4
-输出 [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
-解释 如下图所示,4 皇后问题存在 2 个不同的解法。
+输入:n = 4
+输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
+解释:如下图所示,4 皇后问题存在 2 个不同的解法。
```

#### 5.2.3 解题思路
+##### 思路 1:回溯算法
+
这道题是经典的回溯问题。我们可以按照行序来放置皇后,也就是先放第一行,再放第二行 …… 一直放到最后一行。
对于 `n * n` 的棋盘来说,每一行有 `n` 列,也就有 `n` 种放法可供选择。我们可以尝试选择其中一列,查看是否与之前放置的皇后有冲突,如果没有冲突,则继续在下一行放置皇后。依次类推,直到放置完所有皇后,并且都不发生冲突时,就得到了一个合理的解。
@@ -275,7 +301,7 @@ class Solution:
下面我们根据回溯算法三步走,写出对应的回溯算法。
-1. **明确所有选择**:根据棋盘中当前行的所有列位置上是否选择放置皇后。以 `3 * 3` 大小的棋盘为例,画出决策树,如下图所示。
+1. **明确所有选择**:根据棋盘中当前行的所有列位置上是否选择放置皇后,画出决策树,如下图所示。
- 
@@ -332,11 +358,25 @@ class Solution:
- 当遍历到决策树的叶子节点时,就终止了。也就是在最后一行放置完皇后(即 `row == n`)时,递归停止。
- 递归停止时,将当前符合条件的棋盘转换为答案需要的形式,然后将其存入答案数组 `res` 中即可。
-#### 5.2.4 代码
+##### 思路 1:代码
```Python
class Solution:
- # 判断当前位置 row, col 是否与之前放置的皇后发生冲突
+ res = []
+ def backtrack(self, n: int, row: int, chessboard: List[List[str]]):
+ if row == n:
+ temp_res = []
+ for temp in chessboard:
+ temp_str = ''.join(temp)
+ temp_res.append(temp_str)
+ self.res.append(temp_res)
+ return
+ for col in range(n):
+ if self.isValid(n, row, col, chessboard):
+ chessboard[row][col] = 'Q'
+ self.backtrack(n, row + 1, chessboard)
+ chessboard[row][col] = '.'
+
def isValid(self, n: int, row: int, col: int, chessboard: List[List[str]]):
for i in range(row):
if chessboard[i][col] == 'Q':
@@ -348,7 +388,6 @@ class Solution:
return False
i -= 1
j -= 1
-
i, j = row - 1, col + 1
while i >= 0 and j < n:
if chessboard[i][j] == 'Q':
@@ -357,29 +396,19 @@ class Solution:
j += 1
return True
-
+
def solveNQueens(self, n: int) -> List[List[str]]:
- chessboard = [['.' for _ in range(n)] for _ in range(n)] # 棋盘初始化
+ self.res.clear()
+ chessboard = [['.' for _ in range(n)] for _ in range(n)]
+ self.backtrack(n, 0, chessboard)
+ return self.res
+```
- res = [] # 存放所有符合条件结果的集合
- def backtrack(chessboard: List[List[str]], row: int): # 正在考虑放置第 row 行的皇后
- if row == n: # 遇到终止条件
- path = [] # 当前符合条件的结果
- for ch in chessboard:
- row_str = ''.join(ch)
- path.append(row_str)
- res.append(path) # 将当前符合条件的结果放入集合中
- return
+##### 思路 1:复杂度分析
- for col in range(n): # 枚举可放置皇后的列
- if self.isValid(n, row, col, chessboard): # 如果该位置与之前放置的皇后不发生冲突
- chessboard[row][col] = 'Q' # 选择 row, col 位置放置皇后
- backtrack(chessboard, row + 1) # 递归放置 row + 1 行之后的皇后
- chessboard[row][col] = '.' # 撤销选择 row, col 位置
+- **时间复杂度**:$O(n!)$,其中 $n$ 是皇后数量。
+- **空间复杂度**:$O(n^2)$,其中 $n$ 是皇后数量。递归调用层数不会超过 $n$,每个棋盘的空间复杂度为 $O(n^2)$,所以空间复杂度为 $O(n^2)$。
- backtrack(chessboard, 0)
- return res
-```
## 参考资料
diff --git a/Contents/09.Algorithm-Base/05.Greedy-Algorithm/01.Greedy-Algorithm.md b/Contents/09.Algorithm-Base/05.Greedy-Algorithm/01.Greedy-Algorithm.md
index 56254d7f..4a9114b0 100644
--- a/Contents/09.Algorithm-Base/05.Greedy-Algorithm/01.Greedy-Algorithm.md
+++ b/Contents/09.Algorithm-Base/05.Greedy-Algorithm/01.Greedy-Algorithm.md
@@ -8,15 +8,20 @@
换句话说,贪心算法不从整体最优上加以考虑,而是一步一步进行,每一步只以当前情况为基础,根据某个优化测度做出局部最优选择,从而省去了为找到最优解要穷举所有可能所必须耗费的大量时间。
-当然,使用贪心算法所得到的最终解并不一定就是全局最优解。但是对许多问题来说,确实可以通过局部最优解而得到整体最优解或者是整体最优解的近似解。
+对许多问题来说,可以使用贪心算法,通过局部最优解而得到整体最优解或者是整体最优解的近似解。
-一般来说,这些能够使用贪心算法解决的问题必须满足下面的两个特征:「贪⼼选择性质」和「最优子结构」。
+但并不是所有问题,都可以使用贪心算法的。
+
+一般来说,这些能够使用贪心算法解决的问题必须满足下面的两个特征:
+
+1. **贪⼼选择性质**
+2. **最优子结构**
### 1.2 贪心算法的特征
#### 1.2.1 贪心选择性质
-「贪心选择」:指的是一个问题的全局最优解可以通过一系列局部最优解(贪心选择)来得到。
+> **贪心选择**:指的是一个问题的全局最优解可以通过一系列局部最优解(贪心选择)来得到。
换句话说,当进行选择时,我们直接做出在当前问题中看来最优的选择,而不用去考虑子问题的解。在做出选择之后,才会去求解剩下的子问题,如下图所示。
@@ -26,9 +31,11 @@
#### 1.2.2 最优子结构性质
-「最优子结构」:指的是一个问题的最优解包含其子问题的最优解。
+> **最优子结构**:指的是一个问题的最优解包含其子问题的最优解。
+
+问题的最优子结构性质是该问题能否用贪心算法求解的关键。
-问题的最优子结构性质是该问题能否用贪心算法求解的关键。举个例子,如下图所示,原问题 $S = \lbrace a_1, a_2, a_3, a_4 \rbrace$,在 $a_1$ 步我们通过贪心选择选出一个当前最优解之后,问题就转换为求解子问题 $S_{子问题} = \lbrace a_2, a_3, a_4 \rbrace$。如果原问题 $S$ 的最优解可以由「第 $a_1$ 步通过贪心选择的局部最优解」和「 $S_{子问题}$ 的最优解」构成,则说明该问题满足最优子结构性质。
+举个例子,如下图所示,原问题 $S = \lbrace a_1, a_2, a_3, a_4 \rbrace$,在 $a_1$ 步我们通过贪心选择选出一个当前最优解之后,问题就转换为求解子问题 $S_{子问题} = \lbrace a_2, a_3, a_4 \rbrace$。如果原问题 $S$ 的最优解可以由「第 $a_1$ 步通过贪心选择的局部最优解」和「 $S_{子问题}$ 的最优解」构成,则说明该问题满足最优子结构性质。
也就是说,如果原问题的最优解包含子问题的最优解,则说明该问题满足最优子结构性质。
@@ -40,10 +47,11 @@
### 1.3 贪心算法正确性的证明
-贪心算法最难的部分不在于问题的求解,而在于是正确性的证明。常用的证明方法有「数学归纳法」和「交换论证法」。
+贪心算法最难的部分不在于问题的求解,而在于是正确性的证明。我们常用的证明方法有「数学归纳法」和「交换论证法」。
-- **数学归纳法**:先计算出边界情况(例如 $n = 1$)的最优解,然后再证明对于每个 $n$,$F_{n + 1}$ 都可以由 $F_n$ 推导出。
-- **交换论证法**:从最优解出发,在保证全局最优不变的前提下,如果交换方案中任意两个元素 / 相邻的两个元素后,答案不会变得更好,则可以推定目前的解是最优解。
+> - **数学归纳法**:先计算出边界情况(例如 $n = 1$)的最优解,然后再证明对于每个 $n$,$F_{n + 1}$ 都可以由 $F_n$ 推导出。
+>
+> - **交换论证法**:从最优解出发,在保证全局最优不变的前提下,如果交换方案中任意两个元素 / 相邻的两个元素后,答案不会变得更好,则可以推定目前的解是最优解。
判断一个问题是否通过贪心算法求解,是需要进行严格的数学证明的。但是在日常写题或者算法面试中,不太会要求大家去证明贪心算法的正确性。
@@ -82,14 +90,26 @@
**示例**:
+- 示例 1:
+
+```Python
+输入:g = [1,2,3], s = [1,1]
+输出:1
+解释:你有三个孩子和两块小饼干,3 个孩子的胃口值分别是:1, 2, 3。虽然你有两块小饼干,由于他们的尺寸都是 1,你只能让胃口值是 1 的孩子满足。所以应该输出 1。
+```
+
+- 示例 2:
+
```Python
-输入 g = [1,2,3], s = [1,1]
-输出 1
-解释 你有三个孩子和两块小饼干,3 个孩子的胃口值分别是:1, 2, 3。虽然你有两块小饼干,由于他们的尺寸都是 1,你只能让胃口值是 1 的孩子满足。所以应该输出 1。
+输入: g = [1,2], s = [1,2,3]
+输出: 2
+解释: 你有两个孩子和三块小饼干,2个孩子的胃口值分别是1, 2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出 2。
```
#### 4.1.3 解题思路
+##### 思路 1:贪心算法
+
为了尽可能的满⾜更多的⼩孩,而且一块饼干不能掰成两半,所以我们应该尽量让胃口小的孩子吃小块饼干,这样胃口大的孩子才有大块饼干吃。
所以,从贪心算法的角度来考虑,我们应该按照孩子的胃口从小到大对数组 `g` 进行排序,然后按照饼干的尺寸大小从小到大对数组 `s` 进行排序,并且对于每个孩子,应该选择满足这个孩子的胃口且尺寸最小的饼干。
@@ -108,7 +128,7 @@
2. 如果 `g[index_g] > s[index_s]`,说明当前饼干无法满足当前孩子胃口,则向右移动 `index_s`,判断下一块饼干是否可以满足当前孩子胃口。
3. 遍历完输出答案 `res`。
-#### 4.1.4 代码
+##### 思路 1:代码
```Python
class Solution:
@@ -128,6 +148,11 @@ class Solution:
return res
```
+##### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(m \times \log m + n \times \log n)$,其中 $m$ 和 $n$ 分别是数组 $g$ 和 $s$ 的长度。
+- **空间复杂度**:$O(\log m + \log n)$。
+
### 4.2 无重叠区间
#### 4.2.1 题目链接
@@ -148,15 +173,27 @@ class Solution:
**示例**:
+- 示例 1:
+
```Python
-输入 intervals = [[1,2],[2,3],[3,4],[1,3]]
-输出 1
-解释 移除 [1,3] 后,剩下的区间没有重叠。
+输入:intervals = [[1,2],[2,3],[3,4],[1,3]]
+输出:1
+解释:移除 [1,3] 后,剩下的区间没有重叠。
+```
+
+- 示例 2:
+
+```Python
+输入: intervals = [ [1,2], [1,2], [1,2] ]
+输出: 2
+解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
```
#### 4.2.3 解题思路
-这道题我们可以转换一下思路。原题要求保证移除区间最少,使得剩下的区间互不重叠。换个角度就是:「如何使得剩下互补重叠区间的数目最多」。那么答案就变为了:「总区间个数 - 不重叠区间的最多个数」。我们的问题也变成了求所有区间中不重叠区间的最多个数。
+##### 思路 1:贪心算法
+
+这道题我们可以转换一下思路。原题要求保证移除区间最少,使得剩下的区间互不重叠。换个角度就是:「如何使得剩下互不重叠区间的数目最多」。那么答案就变为了:「总区间个数 - 不重叠区间的最多个数」。我们的问题也变成了求所有区间中不重叠区间的最多个数。
从贪心算法的角度来考虑,我们应该将区间按照结束时间排序。每次选择结束时间最早的区间,然后再在剩下的时间内选出最多的区间。
@@ -173,7 +210,7 @@ class Solution:
1. 如果 `end_pos <= intervals[i][0]`,即 `end_pos` 小于等于区间起始位置,则说明出现了不重叠区间,令不重叠区间数 `count` 加 `1`,`end_pos` 更新为新区间的结束位置。
3. 最终返回「总区间个数 - 不重叠区间的最多个数」即 `len(intervals) - count` 作为答案。
-#### 4.2.4 代码
+##### 思路 1:代码
```Python
class Solution:
@@ -191,6 +228,11 @@ class Solution:
return len(intervals) - count
```
+##### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(n \times \log n)$,其中 $n$ 是区间的数量。
+- **空间复杂度**:$O(\log n)$。
+
## 参考资料
- 【博文】[贪心 - OI Wiki](https://oi-wiki.org/basic/greedy/)
diff --git a/Contents/09.Algorithm-Base/06.Bit-Operation/01.Bit-Operation.md b/Contents/09.Algorithm-Base/06.Bit-Operation/01.Bit-Operation.md
index 1806f18b..4e84074e 100644
--- a/Contents/09.Algorithm-Base/06.Bit-Operation/01.Bit-Operation.md
+++ b/Contents/09.Algorithm-Base/06.Bit-Operation/01.Bit-Operation.md
@@ -1,74 +1,180 @@
## 1. 位运算简介
-> **位运算(Bit Operation)**:在计算机内部,数是以「二进制(Binary)」的形式表示的。位运算就是直接对数的二进制进行计算操作,在程序中使用位运算进行操作,会大大提高程序的性能。
+### 1.1 位运算与二进制简介
-- **二进制数(Binary)**:用 `0` 和 `1` 两个数码来表示的数,它的基数是 `2`,进位规则是「逢二进一」,借位规则是「借一当二」。例如,十进制中的 `1`、`2`、`3`、`4` 对应的二进制数分别为 `001`、`010`、`011`、`100`。
+> **位运算(Bit Operation)**:在计算机内部,数是以「二进制(Binary)」的形式来进行存储。位运算就是直接对数的二进制进行计算操作,在程序中使用位运算进行操作,会大大提高程序的性能。
-二进制数中的每一位数字称为「位(Bit)」, `3` 位所能表示的最大二进制数是 `111`,也就是十进制中的 `7`,即 $1 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = 7$。
+在学习二进制数的位运算之前,我们先来了解一下什么叫做「二进制数」。
-在二进制的基础上,我们可以对二进制数进行相应的位运算。基本的位运算共 `6` 种,分别是:「按位与」、「按位或」、「按位异或」、「按位取反」、「左移」和「右移」。
+
+
+> **二进制数(Binary)**:由 $0$ 和 $1$ 两个数码来表示的数。二进制数中每一个 $0$ 或每一个 $1$ 都称为一个「位(Bit)」。
+
+我们通常使用的十进制数有 $0 \sim 9$ 共 $10$ 个数字,进位规则是「满十进一」。例如:
+
+1. $7_{(10)} + 2_{(10)} = 9_{(10)}$:$7_{(10)}$ 加上 $2_{(10)}$ 等于 $9_{(10)}$。
+2. $9_{(10)} + 2_{(10)} = 11_{(10)}$:$9_{(10)}$ 加上 $2_{(10)}$ 之后个位大于等于 $10$,符合「满十进一」,结果等于 $11_{(10)}$。
+
+而在二进制数中,我们只有 $0$ 和 $1$ 两个数码,它的进位规则是「逢二进一」。例如:
+
+1. $1_{(2)} + 0_{(2)} = 1_{(2)}$:$1_{(2)}$ 加上 $0_{(2)}$ 等于 $1_{(2)}$。
+2. $1_{(2)} + 1_{(2)} = 10_{(2)}$:$1_{(2)}$ 加上 $1_{(2)}$,大于等于 $2$,符合「逢二进一」,结果等于 $10_{(2)}$。
+3. $10_{(2)} + 1_{(2)} = 11_{(2)}$。
+
+### 1.2 二进制数的转换
+
+#### 1.2.1 二进制转十进制数
+
+在十进制数中,数字 $2749_{(10)}$ 可以理解为 $2 \times 1000 + 7 \times 100 + 4 \times 10 + 9 * 1$,相当于 $2 \times 10^3 + 7 \times 10^2 + 4 \times 10^1 + 9 \times 10^0$,即 $2000 + 700 + 40 + 9 = 2749_{(10)}$。
+
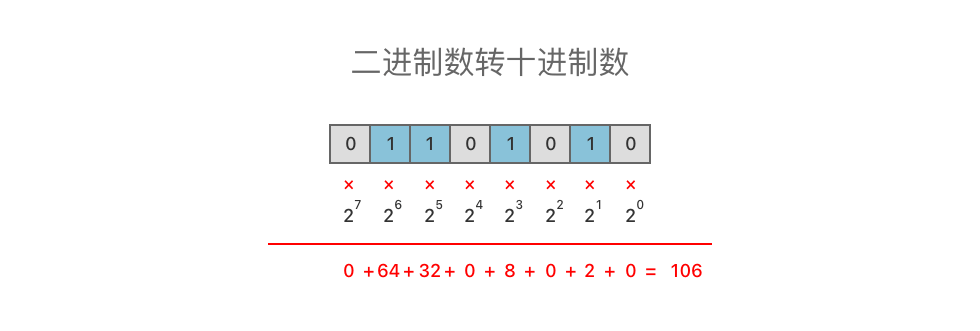
+同理,在二进制数中,$01101010_{(2)}$ 可以看作为 $(0 \times 2^7) + (1 \times 2^6) + (1 \times 2^5) + (0 \times 2^4) + (1 \times 2^3) + (0 \times 2^2) + (1 \times 2^1) + (0 \times 2^0)$,即 $0 + 64 + 32 + 0 + 8 + 0 + 2 + 0 = 106_{(10)}$。
+
+
+
+我们可以通过这样的方式,将一个二进制数转为十进制数。
+
+#### 1.2.2 十进制转二进制数
+
+十进制数转二进制数的方法是:**除二取余,逆序排列法**。
+
+我们以十进制数中的 $106_{(10)}$ 为例。
+
+$\begin{aligned} 106 \div 2 = 53 & \text{(余 0)} \cr 53 \div 2 = 26 & \text{(余 1)} \cr 26 \div 2 = 13 & \text{(余 0)} \cr 13 \div 2 = 6 & \text{(余 1)} \cr 6 \div 2 = 3 & \text{(余 0)} \cr 3 \div 2 = 1 & \text{(余 1)} \cr 1 \div 2 = 0 & \text{(余 1)} \cr 0 \div 2 = 0 & \text{(余 0)} \end{aligned}$
+
+我们反向遍历每次计算的余数,依次是 $0$,$1$,$1$,$0$,$1$,$0$,$1$,$0$,即 $01101010_{(2)}$。
## 2. 位运算基础操作
+在二进制的基础上,我们可以对二进制数进行相应的位运算。基本的位运算共有 $6$ 种,分别是:「按位与运算」、「按位或运算」、「按位异或运算」、「取反运算」、「左移运算」、「右移运算」。
+
+这里的「按位与运算」、「按位或运算」、「按位异或运算」、「左移运算」、「右移运算」是双目运算。
+
+- 「按位与运算」、「按位或运算」、「按位异或运算」是将两个整数作为二进制数,对二进制数表示中的每一位(即二进位)逐一进行相应运算,即双目运算。
+- 「左移运算」、「右移运算」是将左侧整数作为二进制数,将右侧整数作为移动位数,然后对左侧二进制数的全部位进行移位运算,每次移动一位,总共移动右侧整数次位,也是双目运算。
+
+而「取反运算」是单目运算,是对一个整数的二进制数进行的位运算。
+
+我们先来看下这 $6$ 种位运算的规则,再来进行详细讲解。
+
+| 运算符 | 描述 | 规则 |
+| ------ | -------------- | ------------------------------------------------------------ |
+| `&` | 按位与运算符 | 只有对应的两个二进位都为 $1$ 时,结果位才为 $1$。 |
+| `|` | 按位或运算符 | 只要对应的两个二进位有一个为 $1$ 时,结果位就为 $1$。 |
+| `^` | 按位异或运算符 | 对应的两个二进位相异时,结果位为 $1$,二进位相同时则结果位为 $0$。 |
+| `~` | 取反运算符 | 对二进制数的每个二进位取反,使数字 $1$ 变为 $0$,$0$ 变为 $1$。 |
+| `<<` | 左移运算符 | 将二进制数的各个二进位全部左移若干位。`<<` 右侧数字指定了移动位数,高位丢弃,低位补 $0$。 |
+| `>>` | 右移运算符 | 对二进制数的各个二进位全部右移若干位。`>>` 右侧数字指定了移动位数,低位丢弃,高位补 $0$。 |
+
### 2.1 按位与运算
-> **按位与运算(AND)**:按位与运算符 `&` 是双目运算符。其功能是对两个二进制数的每一个二进制位相与。只有对应的两个二进值位都为 `1` 时,结果位才为 `1`。当参与运算的是负数时,参与两个数均以补码出现。
+> **按位与运算(AND)**:按位与运算符为 `&`。其功能是对两个二进制数的每一个二进位进行与运算。
+
+- **按位与运算规则**:只有对应的两个二进位都为 $1$ 时,结果位才为 $1$。
-- 按位与运算规则:
- `1 & 1 = 1`
+
- `1 & 0 = 0`
+
- `0 & 1 = 0`
- - `0 & 0 = 0`
-例如,十进制中的 `3` 和 `5` 进行按位与运算,则结果如图所示:
+ - `0 & 0 = 0`
-
-按位与运算的通常用法:
+举个例子,对二进制数 $01111100_{(2)}$ 与 $00111110_{(2)}$ 进行按位与运算,结果为 $00111100_{(2)}$,如图所示:
-1. **清零**:任何数与 `0` 做按位与运算结果都为 `0`。
- - `(x & 0) == 0`。
-2. **取指定位**:比如要取一个数的低 `4` 位,则只需使用该数与二进制数 `00001111 (后 4 位为 1)`做按位与运算,结果就是这个数的低 `4` 位的值。
-3. **奇偶判断**:通过与 `1` 进行按位与运算,即可判断某个数是奇数还是偶数。
- - `(x & 1) == 0` 为偶数,`(x & 1) == 1` 为奇数。
+
### 2.2 按位或运算
-> **按位或运算(OR)**:按位或运算符 `|` 是双目运算符。其功能对两个二进制数的每一个二进制位相或。只要对应的 `2` 个二进位有一个为 `1` 时,结果位就为 `1`。当参与运算的是负数时,参与两个数均以补码出现。
+> **按位或运算(OR)**:按位或运算符为 `|`。其功能对两个二进制数的每一个二进位进行或运算。
-- 按位或运算规则:
+- **按位或运算规则**:只要对应的两个二进位有一个为 $1$ 时,结果位就为 $1$。
- `1 | 1 = 1`
- `1 | 0 = 1`
- `0 | 1 = 1`
- `0 | 0 = 0`
-例如,十进制中的 `3` 和 `5` 进行按位或运算,则结果如图所示:
-
-
-按位或运算的通常用法:
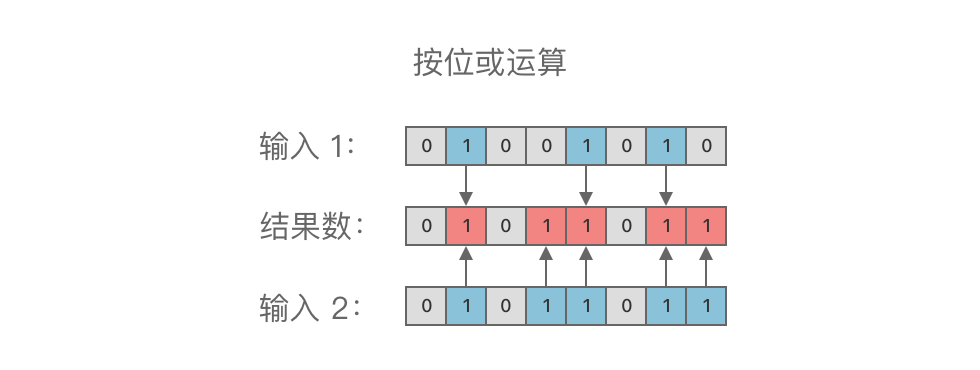
+举个例子,对二进制数 $01001010_{(2)}$ 与 $01011011_{(2)}$ 进行按位或运算,结果为 $01011011_{(2)}$,如图所示:
-1. **将某位设置为 `1`**:比如需要将一个数的低 `4` 位设置为 `1`,则只需使用该数与二进制数 `00001111 (后 4 位为 1)` 做按位或运算即可得到。
+
### 2.3 按位异或运算
-> **按位异或运算(XOR)**:按位异或运算符 `^` 是双目运算符。其功能是对两个二进制数的每一个二进制位相异或。如果某位不相同则该位为 `1`,如果某位相同则该位为 `0`。当参与运算的是负数时,参与两个数均以补码出现。
+> **按位异或运算(XOR)**:按位异或运算符为 `^`。其功能是对两个二进制数的每一个二进位进行异或运算。
+
+- **按位异或运算规则**:对应的两个二进位相异时,结果位为 $1$,二进位相同时则结果位为 $0$。
+- `0 ^ 0 = 0`
+
+- `1 ^ 0 = 1`
+
+- `0 ^ 1 = 1`
+
+- `1 ^ 1 = 0`
+
+
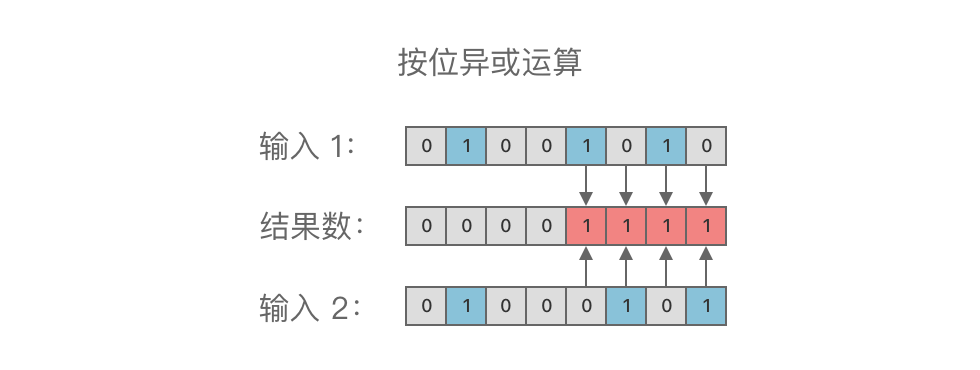
+举个例子,对二进制数 $01001010_{(2)}$ 与 $01000101_{(2)}$ 进行按位异或运算,结果为 $00001111_{(2)}$,如图所示:
+
+
+
+### 2.4 取反运算
+
+>**取反运算(NOT)**:取反运算符为 `~`。其功能是对一个二进制数的每一个二进位进行取反运算。
+
+- **取反运算规则**:使数字 $1$ 变为 $0$,$0$ 变为 $1$。
+ - `~0 = 1`
+ - `~1 = 0`
+
+举个例子,对二进制数 $01101010_{(2)}$ 进行取反运算,结果如图所示:
+
+
+
+### 2.5 左移运算和右移运算
+
+> **左移运算(SHL)**: 左移运算符为 `<<`。其功能是对一个二进制数的各个二进位全部左移若干位(高位丢弃,低位补 $0$)。
-- 按位异或运算规则:
- - `0 ^ 0 = 0`
- - `1 ^ 0 = 1`
- - `0 ^ 1 = 1`
- - `1 ^ 1 = 0`
+举个例子,对二进制数 $01101010_{(2)}$ 进行左移 $1$ 位运算,结果为 $11010100_{(2)}$,如图所示:
-例如,十进制中的 `3` 和 `5` 进行按位异或运算,则结果如图所示:
+
-
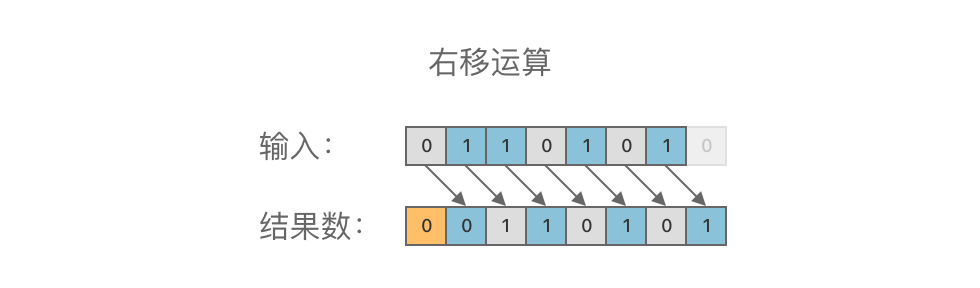
+> **右移运算(SHR)**: 右移运算符为 `>>`。其功能是对一个二进制数的各个二进位全部右移若干位(低位丢弃,高位补 $0$)。
-按位异或运算的通常用法:
+举个例子,对二进制数 $01101010_{(2)}$ 进行右移 $1$ 位运算,结果为 $00110101_{(2)}$,如图所示:
-1. **翻转指定位**:比如需要将一个数的低 `4` 位进行反转,则只需使用该数与二进制数 `00001111 (后 4 位为 1)` 做按位异或运算即可得到。
-2. **与 `0` 相异或值不变**:一个数与 `0` 做按位异或运算的结果不变。例如,`10101100 ^ 00000000 = 10101100`。
-3. **交换两个数**:通过按位异或运算可以实现交换两个数的目的。
+
+
+## 3. 位运算的应用
+
+### 3.1 位运算的常用操作
+
+#### 3.1.1 判断整数奇偶
+
+一个整数,只要是偶数,其对应二进制数的末尾一定为 $0$;只要是奇数,其对应二进制数的末尾一定为 $1$。所以,我们通过与 $1$ 进行按位与运算,即可判断某个数是奇数还是偶数。
+
+1. `(x & 1) == 0` 为偶数。
+2. `(x & 1) == 1` 为奇数。
+
+#### 3.1.2 二进制数选取指定位
+
+如果我们想要从一个二进制数 $X$ 中取出某几位,使取出位置上的二进位保留原值,其余位置为 $0$,则可以使用另一个二进制数 $Y$,使该二进制数上对应取出位置为 $1$,其余位置为 $0$。然后令两个数进行按位与运算(`X & Y`),即可得到想要的数。
+
+举个例子,比如我们要取二进制数 $X = 01101010_{(2)}$ 的末尾 $4$ 位,则只需将 $X = 01101010_{(2)}$ 与 $Y = 00001111_{(2)}$ (末尾 $4$ 位为 $1$,其余位为 $0$) 进行按位与运算,即 `01101010 & 00001111 == 00001010`。其结果 $00001010$ 就是我们想要的数(即二进制数 $01101010_{(2)}$ 的末尾 $4$ 位)。
+
+#### 3.1.3 将指定位设置为 $1$
+
+如果我们想要把一个二进制数 $X$ 中的某几位设置为 $1$,其余位置保留原值,则可以使用另一个二进制数 $Y$,使得该二进制上对应选取位置为 $1$,其余位置为 $0$。然后令两个数进行按位或运算(`X | Y`),即可得到想要的数。
+
+举个例子,比如我们想要将二进制数 $X = 01101010_{(2)}$ 的末尾 $4$ 位设置为 $1$,其余位置保留原值,则只需将 $X = 01101010_{(2)}$ 与 $Y = 00001111_{(2)}$(末尾 $4$ 位为 $1$,其余位为 $0$)进行按位或运算,即 `01101010 | 00001111 = 01101111`。其结果 $01101111$ 就是我们想要的数(即将二进制数 $01101010_{(2)}$ 的末尾 $4$ 位设置为 $1$,其余位置保留原值)。
+
+#### 3.1.4 反转指定位
+
+如果我们想要把一个二进制数 $X$ 的某几位进行反转,则可以使用另一个二进制数 $Y$,使得该二进制上对应选取位置为 $1$,其余位置为 $0$。然后令两个数进行按位异或运算(`X ^ Y`),即可得到想要的数。
+
+举个例子,比如想要将二进制数 $X = 01101010_{(2)}$ 的末尾 $4$ 位进行反转,则只需将 $X = 01101010_{(2)}$ 与 $Y = 00001111_{(2)}$(末尾 $4$ 位为 $1$,其余位为 $0$)进行按位异或运算,即 `01101010 ^ 00001111 = 01100101`。其结果 $01100101$ 就是我们想要的数(即将二进制数 $X = 01101010_{(2)}$ 的末尾 $4$ 位进行反转)。
+
+#### 3.1.5 交换两个数
+
+通过按位异或运算可以实现交换两个数的目的(只能用于交换两个整数)。
```Python
a, b = 10, 20
@@ -78,37 +184,45 @@ a ^= b
print(a, b)
```
-### 2.4 按位取反运算
+#### 3.1.6 将二进制最右侧为 $1$ 的二进位改为 $0$
->**按位取反运算(NOT)**:按位取反运算符 `~` 是单目运算符。其功能是对一个二进制数的每一个二进制位取反。使数字 `1` 变为 `0`,`0` 变为 `1`。当参与运算的是负数时,参与的该数以补码出现。
+如果我们想要将一个二进制数 $X$ 最右侧为 $1$ 的二进制位改为 $0$,则只需通过 `X & (X - 1)` 的操作即可完成。
-- 按位取反运算规则:
- - `~0 = 1`
- - `~1 = 0`
+比如 $X = 01101100_{(2)}$,$X - 1 = 01101011_{(2)}$,则 `X & (X - 1) == 01101100 & 01101011 == 01101000`,结果为 $01101000_{(2)}$(即将 $X$ 最右侧为 $1$ 的二进制为改为 $0$)。
-例如,十进制中的 `3` 进行按位取反运算,则结果如图所示:
+#### 3.1.7 计算二进制中二进位为 $1$ 的个数
-
+从 3.1.6 中得知,通过 `X & (X - 1)` 我们可以将二进制 $X$ 最右侧为 $1$ 的二进制位改为 $0$,那么如果我们不断通过 `X & (X - 1)` 操作,最终将二进制 $X$ 变为 $0$,并统计执行次数,则可以得到二进制中二进位为 $1$ 的个数。
-### 2.5 按位左移运算
+具体代码如下:
-> **按位左移运算(SHL)**: 按位左移运算符 `<<` 是双目运算符。其功能是对一个二进制数的各个二进制位全部左移若干位(左边的二进制位丢弃,右边末尾补 `0`)。
+```Python
+class Solution:
+ def hammingWeight(self, n: int) -> int:
+ cnt = 0
+ while n:
+ n = n & (n - 1)
+ cnt += 1
+ return cnt
+```
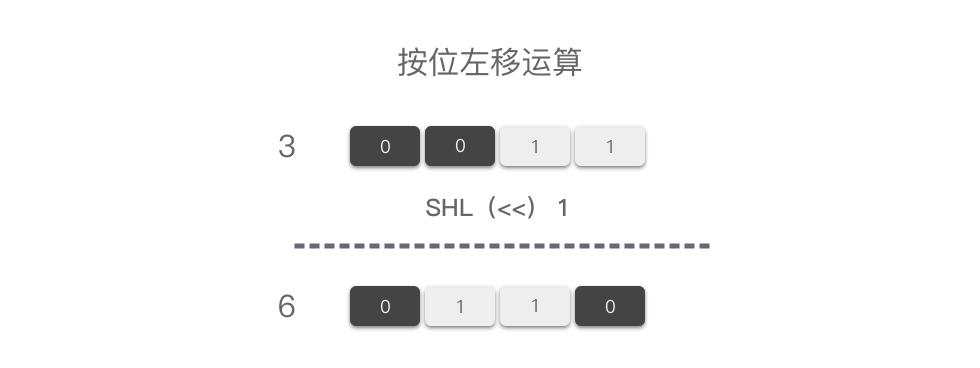
-例如,十进制中的 `3` 进行左移 `1` 位运算,则结果如图所示:
+#### 3.1.8 判断某数是否为 $2$ 的幂次方
-
+通过判断 `X & (X - 1) == 0` 是否成立,即可判断 $X$ 是否为 $2$ 的幂次方。
-### 2.6 按位右移运算
+这是因为:
-> **按位右移运算(SHR)**: 按位右移运算符 `>>` 是双目运算符。其功能是对一个二进制数的各个二进制位全部右移若干位(右边的二进制位丢弃,正数左边开补 `0`,负数左边补 `1`)。
+1. 凡是 $2$ 的幂次方,其二进制数的某一高位为 $1$,并且仅此高位为 $1$,其余位都为 $0$。比如:$4_{(10)} = 00000100_{(2)}$、$8_{(10)} = 00001000_{(2)}$。
+2. 不是 $2$ 的幂次方,其二进制数存在多个值为 $1$ 的位。比如:$5_{10} = 00000101_{(2)}$、$6_{10} = 00000110_{(2)}$。
-例如,十进制中的 `3` 进行右移 `1` 位运算,则结果如图所示:
+接下来我们使用 `X & (X - 1)` 操作,将原数对应二进制数最右侧为 $1$ 的二进位改为 $0$ 之后,得到新值:
-
+1. 如果原数是 $2$ 的幂次方,则通过 `X & (X - 1)` 操作之后,新值所有位都为 $0$,值为 $0$。
+2. 如果该数不是 $2$ 的幂次方,则通过 `X & (X - 1)` 操作之后,新值仍存在不为 $0$ 的位,值肯定不为 $0$。
-## 2. 位运算的应用
+所以我们可以通过是否为 $0$ 即可判断该数是否为 $2$ 的幂次方。
-### 2.1 位运算的常用应用
+### 3.2 位运算的常用操作总结
| 功 能 | 位运算 | 示例 |
| ----------------------------------------- | -------------------------------- | ---------------------- |
@@ -133,11 +247,72 @@ print(a, b)
| **去掉右边起第一个 `1` 的左边** | x & (x ^ (x - 1)) 或 x & (-x) | `100101000 -> 1000` |
| **从右边开始,把最后一个 `1` 改写成 `0`** | x & (x - 1) | `100101000 -> 100100000` |
-### 2.1 Brian Kernighan 算法
+### 3.3 二进制枚举子集
+除了上面的这些常见操作,我们经常常使用二进制数第 $1 \sim n$ 位上 $0$ 或 $1$ 的状态来表示一个由 $1 \sim n$ 组成的集合。也就是说通过二进制来枚举子集。
+#### 3.3.1 二进制枚举子集简介
+
+先来介绍一下「子集」的概念。
+
+- **子集**:如果集合 $A$ 的任意一个元素都是集合 $S$ 的元素,则称集合 $A$ 是集合 $S$ 的子集。可以记为 $A \in S$。
+
+有时候我们会遇到这样的问题:给定一个集合 $S$,枚举其所有可能的子集。
+
+枚举子集的方法有很多,这里介绍一种简单有效的枚举方法:「二进制枚举子集算法」。
+
+对于一个元素个数为 $n$ 的集合 $S$ 来说,每一个位置上的元素都有选取和未选取两种状态。我们可以用数字 $1$ 来表示选取该元素,用数字 $0$ 来表示不选取该元素。
+
+那么我们就可以用一个长度为 $n$ 的二进制数来表示集合 $S$ 或者表示 $S$ 的子集。其中二进制的每一个二进位都对应了集合中某一个元素的选取状态。对于集合中第 $i$ 个元素来说,二进制对应位置上的 $1$ 代表该元素被选取,$0$ 代表该元素未被选取。
+
+举个例子,比如长度为 $5$ 的集合 $S = \left \{ 5, 4, 3, 2, 1 \right \}$,我们可以用一个长度为 $5$ 的二进制数来表示该集合。
+
+比如二进制数 $11111_{(2)}$ 就表示选取集合的第 $1$ 位、第 $2$ 位、第 $3$ 位、第 $4$ 位、第 $5$ 位元素,也就是集合 $\left \{ 5, 4, 3, 2, 1 \right \}$,即集合 $S$ 本身。如下表所示:
+
+| 集合 S 中元素位置 | 5 | 4 | 3 | 2 | 1 |
+| :---------------- | :--: | :--: | :--: | :--: | :--: |
+| 二进位对应值 | 1 | 1 | 1 | 1 | 1 |
+| 对应选取状态 | 选取 | 选取 | 选取 | 选取 | 选取 |
+
+再比如二进制数 $10101_{(2)}$ 就表示选取集合的第 $1$ 位、第 $3$ 位、第 $5$ 位元素,也就是集合 $\left \{5, 3, 1 \right \}$。如下表所示:
+
+| 集合 S 中元素位置 | 5 | 4 | 3 | 2 | 1 |
+| :---------------- | :--: | :----: | :--: | :----: | :--: |
+| 二进位对应值 | 1 | 0 | 1 | 0 | 1 |
+| 对应选取状态 | 选取 | 未选取 | 选取 | 未选取 | 选取 |
+
+再比如二进制数 $01001_{(2)}$ 就表示选取集合的第 $1$ 位、第 $4$ 位元素,也就是集合 $\left \{4, 1 \right \}$。如下标所示:
+
+| 集合 S 中元素位置 | 5 | 4 | 3 | 2 | 1 |
+| :---------------- | :----: | :--: | :----: | :----: | :--: |
+| 二进位对应值 | 0 | 1 | 0 | 0 | 1 |
+| 对应选取状态 | 未选取 | 选取 | 未选取 | 未选取 | 选取 |
+
+通过上面的例子我们可以得到启发:对于长度为 $5$ 的集合 $S$ 来说,我们只需要从 $00000 \sim 11111$ 枚举一次(对应十进制为 $0 \sim 2^5 - 1$)即可得到长度为 $5$ 的集合 $S$ 的所有子集。
+
+我们将上面的例子拓展到长度为 $n$ 的集合 $S$。可以总结为:
+
+- 对于长度为 $n$ 的集合 $S$ 来说,只需要枚举 $0 \sim 2^n - 1$(共 $2^n$ 种情况),即可得到集合 $S$ 的所有子集。
+
+#### 3.3.2 二进制枚举子集代码
+
+```Python
+class Solution:
+ def subsets(self, S): # 返回集合 S 的所有子集
+ n = len(S) # n 为集合 S 的元素个数
+ sub_sets = [] # sub_sets 用于保存所有子集
+ for i in range(1 << n): # 枚举 0 ~ 2^n - 1
+ sub_set = [] # sub_set 用于保存当前子集
+ for j in range(n): # 枚举第 i 位元素
+ if i >> j & 1: # 如果第 i 为元素对应二进位删改为 1,则表示选取该元素
+ sub_set.append(S[j]) # 将选取的元素加入到子集 sub_set 中
+ sub_sets.append(sub_set) # 将子集 sub_set 加入到所有子集数组 sub_sets 中
+ return sub_sets # 返回所有子集
+```
## 参考资料
- 【博文】[Python 中的按位运算符 |【生长吧!Python!】- 云社区 - 华为云](https://bbs.huaweicloud.com/blogs/280901)
-- 【博文】[一文读懂位运算的使用 - 小黑说 Java - 掘金](https://juejin.cn/post/7011407264581943326)
\ No newline at end of file
+- 【博文】[一文读懂位运算的使用 - 小黑说 Java - 掘金](https://juejin.cn/post/7011407264581943326)
+- 【博文】[枚举排列和枚举子集 - CUC ACM-Wiki](https://cuccs.github.io/acm-wiki/search/enumeration/)
+- 【博文】[Swift 运算符 | 菜鸟教程](https://www.runoob.com/swift/swift-operators.html)
\ No newline at end of file
diff --git a/Contents/09.Algorithm-Base/06.Bit-Operation/02.Bit-Operation-List.md b/Contents/09.Algorithm-Base/06.Bit-Operation/02.Bit-Operation-List.md
index 24e0f2f7..27603ad1 100644
--- a/Contents/09.Algorithm-Base/06.Bit-Operation/02.Bit-Operation-List.md
+++ b/Contents/09.Algorithm-Base/06.Bit-Operation/02.Bit-Operation-List.md
@@ -17,4 +17,6 @@
| 0268 | [丢失的数字](https://leetcode.cn/problems/missing-number/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0268.%20%E4%B8%A2%E5%A4%B1%E7%9A%84%E6%95%B0%E5%AD%97.md) | 位运算、数组、数学 | 简单 |
| 1349 | 参加考试的最大学生数 | | | |
| 0645 | 错误的集合 | | | |
+| 0078 | [子集](https://leetcode.cn/problems/subsets/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0078.%20%E5%AD%90%E9%9B%86.md) | 位运算、数组、回溯算法 | 中等 |
+| 0090 | [子集 II](https://leetcode.cn/problems/subsets-ii/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0090.%20%E5%AD%90%E9%9B%86%20II.md) | 位运算、数组、回溯 | 中等 |
diff --git a/README.md b/README.md
index acc0c9e5..090b518c 100644
--- a/README.md
+++ b/README.md
@@ -254,4 +254,4 @@
- [动态规划优化题目](./Contents/10.Dynamic-Programming/11.DP-Optimization/04.DP-Optimization-List.md)
## 11. 附加内容
-## [12. LeetCode 题解(已完成 742 道)](./Contents/00.Introduction/04.Solutions-List.md)
\ No newline at end of file
+## [12. LeetCode 题解(已完成 746 道)](./Contents/00.Introduction/04.Solutions-List.md)
\ No newline at end of file
diff --git "a/Solutions/0017. \347\224\265\350\257\235\345\217\267\347\240\201\347\232\204\345\255\227\346\257\215\347\273\204\345\220\210.md" "b/Solutions/0017. \347\224\265\350\257\235\345\217\267\347\240\201\347\232\204\345\255\227\346\257\215\347\273\204\345\220\210.md"
index eeab94f8..04858730 100644
--- "a/Solutions/0017. \347\224\265\350\257\235\345\217\267\347\240\201\347\232\204\345\255\227\346\257\215\347\273\204\345\220\210.md"
+++ "b/Solutions/0017. \347\224\265\350\257\235\345\217\267\347\240\201\347\232\204\345\255\227\346\257\215\347\273\204\345\220\210.md"
@@ -5,17 +5,42 @@
## 题目大意
-给定一个只包含数字 2~9 的字符串,返回它在九宫格键盘上所能表示的所有字母组合。答案可以按 「任意顺序」返回。
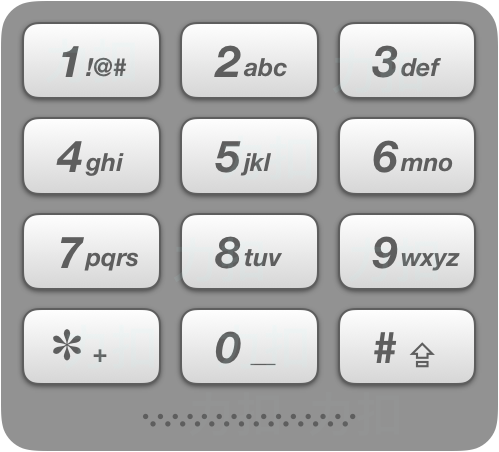
+**描述**:给定一个只包含数字 2~9 的字符串 `digits`。给出数字到字母的映射如下(与电话按键相同)。注意 $1$ 不对应任何字母。
-
+
+
+**要求**:返回字符串 `digits` 在九宫格键盘上所能表示的所有字母组合。答案可以按 「任意顺序」返回。
+
+**说明**:
+
+- $0 \le digits.length \le 4$。
+- `digits[i]` 是范围 $2 \sim 9$ 的一个数字。
+
+**示例**:
+
+- 示例 1:
+
+```Python
+输入:digits = "23"
+输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
+```
+
+- 示例 2:
+
+```Python
+输入:digits = "2"
+输出:["a","b","c"]
+```
## 解题思路
+### 思路 1:回溯算法 + 哈希表
+
用哈希表保存每个数字键位对应的所有可能的字母,然后进行回溯操作。
回溯过程中,维护一个字符串 combination,表示当前的字母排列组合。初始字符串为空,每次取电话号码的一位数字,从哈希表中取出该数字所对应的所有字母,并将其中一个插入到 combination 后面,然后继续处理下一个数字,知道处理完所有数字,得到一个完整的字母排列。开始进行回退操作,遍历其余的字母排列。
-## 代码
+### 思路 1:代码
```Python
class Solution:
@@ -47,3 +72,8 @@ class Solution:
return combinations
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(3^m \times 4^n)$,其中 $m$ 是 `digits` 中对应 $3$ 个字母的数字个数,$m$ 是 `digits` 中对应 $4$ 个字母的数字个数。
+- **空间复杂度**:$O(m + n)$。
+
diff --git "a/Solutions/0023. \345\220\210\345\271\266K\344\270\252\345\215\207\345\272\217\351\223\276\350\241\250.md" "b/Solutions/0023. \345\220\210\345\271\266K\344\270\252\345\215\207\345\272\217\351\223\276\350\241\250.md"
index 6de51d4e..0fcce4f5 100644
--- "a/Solutions/0023. \345\220\210\345\271\266K\344\270\252\345\215\207\345\272\217\351\223\276\350\241\250.md"
+++ "b/Solutions/0023. \345\220\210\345\271\266K\344\270\252\345\215\207\345\272\217\351\223\276\350\241\250.md"
@@ -44,7 +44,7 @@
## 解题思路
-### 思路 1:分治
+### 思路 1:分治算法
分而治之的思想。将链表数组不断二分,转为规模为二分之一的子问题,然后再进行归并排序。
diff --git "a/Solutions/0040. \347\273\204\345\220\210\346\200\273\345\222\214 II.md" "b/Solutions/0040. \347\273\204\345\220\210\346\200\273\345\222\214 II.md"
index 6a503017..84b3af6b 100644
--- "a/Solutions/0040. \347\273\204\345\220\210\346\200\273\345\222\214 II.md"
+++ "b/Solutions/0040. \347\273\204\345\220\210\346\200\273\345\222\214 II.md"
@@ -5,17 +5,51 @@
## 题目大意
-给定一个数组 `candidates` 和一个目标数 `target`,找出 `candidates` 中所有可以使数字和为目标数 `target` 的组合。
+**描述**:给定一个数组 `candidates` 和一个目标数 `target`。
-数组 `candidates` 中的数字在每个组合中只能使用一次,且 `1 ≤ candidates[i] ≤ 50`。
+**要求**:找出 `candidates` 中所有可以使数字和为目标数 `target` 的组合。
+
+**说明**:
+
+- 数组 `candidates` 中的数字在每个组合中只能使用一次。
+- $1 \le candidates.length \le 100$。
+- $1 \le candidates[i] \le 50$。
+
+**示例**:
+
+- 示例 1:
+
+```Python
+输入: candidates = [10,1,2,7,6,1,5], target = 8,
+输出:
+[
+[1,1,6],
+[1,2,5],
+[1,7],
+[2,6]
+]
+```
+
+- 示例 2:
+
+```Python
+输入: candidates = [2,5,2,1,2], target = 5,
+输出:
+[
+[1,2,2],
+[5]
+]
+```
## 解题思路
+### 思路 1:回溯算法
+
跟「[0039. 组合总和](https://leetcode.cn/problems/combination-sum/)」不一样的地方在于本题不能有重复组合,所以关键步骤在于去重。
-在回溯遍历的时候,下一层递归的 start_index 要从当前节点的后一位开始遍历,即 i + 1 位开始。而且统一递归层不能使用相同的元素,即需要增加一句判断 `if i > start_index and candidates[i] == candidates[i - 1]: continue`。
+在回溯遍历的时候,下一层递归的 `start_index` 要从当前节点的后一位开始遍历,即 `i + 1` 位开始。而且统一递归层不能使用相同的元素,即需要增加一句判断 `if i > start_index and candidates[i] == candidates[i - 1]: continue`。
-## 代码
+### 思路 1:代码
```Python
class Solution:
@@ -47,3 +81,8 @@ class Solution:
return self.res
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(2^n \times n)$,其中 $n$ 是数组 `candidates` 的元素个数,$2^n$ 指的是所有状态数。
+- **空间复杂度**:$O(target)$,递归函数需要用到栈空间,栈空间取决于递归深度,最坏情况下递归深度为 $O(target)$,所以空间复杂度为 $O(target)$。
+
diff --git "a/Solutions/0047. \345\205\250\346\216\222\345\210\227 II.md" "b/Solutions/0047. \345\205\250\346\216\222\345\210\227 II.md"
index 24f4f9b7..cfb48c60 100644
--- "a/Solutions/0047. \345\205\250\346\216\222\345\210\227 II.md"
+++ "b/Solutions/0047. \345\205\250\346\216\222\345\210\227 II.md"
@@ -5,17 +5,46 @@
## 题目大意
-给定一个可包含重复数字的序列 `nums` ,按任意顺序返回所有不重复的全排列。
+**描述**:给定一个可包含重复数字的序列 `nums`。
+
+**要求**:按任意顺序返回所有不重复的全排列。
+
+**说明**:
+
+- $1 \le nums.length \le 8$。
+- $-10 \le nums[i] \le 10$。
+
+**示例**:
+
+- 示例 1:
+
+```Python
+输入:nums = [1,1,2]
+输出:[[1,1,2],[1,2,1],[2,1,1]]
+```
+
+- 示例 2:
+
+```Python
+输入:nums = [1,2,3]
+输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
+```
## 解题思路
-这道题跟「[0046. 全排列](https://leetcode.cn/problems/permutations/)」不一样的地方在于增加了序列中的元素可重复这一条件。这就涉及到了去重。先对 `nums` 进行排序,然后使用 visited 数组标记该元素在当前排列中是否被访问过。若未被访问过则将其加入排列中,并在访问后将该元素变为未访问状态。
+### 思路 1:回溯算法
+
+这道题跟「[0046. 全排列](https://leetcode.cn/problems/permutations/)」不一样的地方在于增加了序列中的元素可重复这一条件。这就涉及到了如何去重。
+
+我们可以先对数组 `nums` 进行排序,然后使用一个数组 `visited` 标记该元素在当前排列中是否被访问过。
+
+如果未被访问过则将其加入排列中,并在访问后将该元素变为未访问状态。
然后再递归遍历下一层元素之前,增加一句语句进行判重:`if i > 0 and nums[i] == nums[i - 1] and not visited[i - 1]: continue`。
-然后进行回溯遍历。
+然后再进行回溯遍历。
-## 代码
+### 思路 1:代码
```Python
class Solution:
@@ -45,3 +74,8 @@ class Solution:
return self.res
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(n \times n!)$,其中 $n$ 为数组 `nums` 的元素个数。
+- **空间复杂度**:$O(n)$。
+
diff --git a/Solutions/0050. Pow(x, n).md b/Solutions/0050. Pow(x, n).md
index 941072dc..38e0e29e 100644
--- a/Solutions/0050. Pow(x, n).md
+++ b/Solutions/0050. Pow(x, n).md
@@ -5,21 +5,56 @@
## 题目大意
-给定浮点数 x 和整数 n,计算 $x^n$。
+**描述**:给定浮点数 $x$ 和整数 $n$。
+
+**要求**:计算 $x$ 的 $n$ 次方(即 $x^n$)。
+
+**说明**:
+
+- $-100.0 < x < 100.0$。
+- $-2^{31} \le n \le 2^{31} - 1$。
+- $n$ 是一个整数。
+- $-10^4 \le x^n \le 10^4$。
+
+**示例**:
+
+- 示例 1:
+
+```Python
+输入:x = 2.00000, n = 10
+输出:1024.00000
+```
+
+- 示例 2:
+
+```Python
+输入:x = 2.00000, n = -2
+输出:0.25000
+解释:2-2 = 1/22 = 1/4 = 0.25
+```
## 解题思路
-常规方法是直接将 x 累乘 n 次得出结果,时间复杂度为 $O(n)$。可以利用快速幂来减少时间复杂度。
+### 思路 1:分治算法
+
+常规方法是直接将 $x$ 累乘 $n$ 次得出结果,时间复杂度为 $O(n)$。
+
+我们可以利用分治算法来减少时间复杂度。
-如果 n 为偶数,$x^n = x^{n/2} * x^{n/2}$。如果 n 为奇数,$x^n = x * x^{(n-1)/2} * x^{(n-1)/2}$。
+根据 $n$ 的奇偶性,我们可以得到以下结论:
-$x^(n/2)$ 又可以继续向下递归划分。则我们可以利用低纬度的幂计算结果,来得到高纬度的幂计算结果。
+1. 如果 $n$ 为偶数,$x^n = x^{n / 2} \times x^{n / 2}$。
+2. 如果 $n$ 为奇数,$x^n = x \times x^{(n - 1) / 2} \times x^{(n - 1) / 2}$。
-这样递归求解,时间复杂度为 $O(logn)$,并且递归也可以转为递推来做。
+$x^{(n / 2)}$ 或 $x^{(n - 1) / 2}$ 又可以继续向下递归划分。
-需要注意如果 n 为负数,可以转换为 $\frac{1}{x} ^{(-n)}$。
+则我们可以利用低纬度的幂计算结果,来得到高纬度的幂计算结果。
-## 代码
+这样递归求解,时间复杂度为 $O(\log n)$,并且递归也可以转为递推来做。
+
+需要注意如果 $n$ 为负数,可以转换为 $\frac{1}{x} ^{(-n)}$。
+
+### 思路 1:代码
```Python
class Solution:
@@ -38,3 +73,8 @@ class Solution:
return res
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(\log n)$。
+- **空间复杂度**:$O(1)$。
+
diff --git "a/Solutions/0053. \346\234\200\345\244\247\345\255\220\346\225\260\347\273\204\345\222\214.md" "b/Solutions/0053. \346\234\200\345\244\247\345\255\220\346\225\260\347\273\204\345\222\214.md"
index b4e7873f..1d5151b6 100644
--- "a/Solutions/0053. \346\234\200\345\244\247\345\255\220\346\225\260\347\273\204\345\222\214.md"
+++ "b/Solutions/0053. \346\234\200\345\244\247\345\255\220\346\225\260\347\273\204\345\222\214.md"
@@ -110,4 +110,56 @@ class Solution:
### 思路 2:复杂度分析
- **时间复杂度**:$O(n)$,其中 $n$ 为数组 `nums` 的元素个数。
-- **空间复杂度**:$O(1)$。
\ No newline at end of file
+- **空间复杂度**:$O(1)$。
+
+### 思路 3:分治算法
+
+我们将数组 `nums` 根据中心位置分为左右两个子数组。则具有最大和的连续子数组可能存在以下 $3$ 种情况:
+
+1. 具有最大和的连续子数组在左子数组中。
+2. 具有最大和的连续子数组在右子数组中。
+3. 具有最大和的连续子数组跨过中心位置,一部分在左子数组中,另一部分在右子树组中。
+
+那么我们要求出具有最大和的连续子数组的最大和,则分别对上面 $3$ 种情况求解即可。具体步骤如下:
+
+1. 将数组 `nums` 根据中心位置递归分为左右两个子数组,直到所有子数组长度为 $1$。
+2. 长度为 $1$ 的子数组最大和肯定是数组中唯一的数,将其返回即可。
+3. 求出左子数组的最大和 `left_max`。
+4. 求出右子树组的最大和 `right_max`。
+5. 求出跨过中心位置,一部分在左子数组中,另一部分在右子树组的子数组最大和 `left_total + right_total`。
+6. 求出 $3$、$4$、$5$ 中的最大值,即为当前数组的最大和,将其返回即可。
+
+### 思路 3:代码
+
+```Python
+class Solution:
+ def maxSubArray(self, nums: List[int]) -> int:
+ def max_sub_array(low, high):
+ if low == high:
+ return nums[low]
+
+ mid = low + (high - low) // 2
+ left_max = max_sub_array(low, mid)
+ right_max = max_sub_array(mid + 1, high)
+
+ total = 0
+ left_total = -inf
+ for i in range(mid, low - 1, -1):
+ total += nums[i]
+ left_total = max(left_total, total)
+
+ total = 0
+ right_total = -inf
+ for i in range(mid + 1, high + 1):
+ total += nums[i]
+ right_total = max(right_total, total)
+
+ return max(left_max, right_max, left_total + right_total)
+
+ return max_sub_array(0, len(nums) - 1)
+```
+
+### 思路 3:复杂度分析
+
+- **时间复杂度**:$O(n)$。
+- **空间复杂度**:$O(\log n)$。
\ No newline at end of file
diff --git "a/Solutions/0055. \350\267\263\350\267\203\346\270\270\346\210\217.md" "b/Solutions/0055. \350\267\263\350\267\203\346\270\270\346\210\217.md"
index 843e9d2d..b124d4f6 100644
--- "a/Solutions/0055. \350\267\263\350\267\203\346\270\270\346\210\217.md"
+++ "b/Solutions/0055. \350\267\263\350\267\203\346\270\270\346\210\217.md"
@@ -5,19 +5,89 @@
## 题目大意
-给定一个非负整数数组 nums,数组中每个元素代表在该位置可以跳跃的最大长度。
+**描述**:给定一个非负整数数组 `nums`,数组中每个元素代表在该位置可以跳跃的最大长度。开始位置位于数组的第一个下标处。
-开始位置为数组的第一个下标处。要求判断是否能够到达最后一个下标。
+**要求**:判断是否能够到达最后一个下标。
+
+**说明**:
+
+- $1 \le nums.length \le 3 \times 10^4$。
+- $0 \le nums[i] \le 10^5$。
+
+**示例**:
+
+- 示例 1:
+
+```Python
+输入:nums = [2,3,1,1,4]
+输出:true
+解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
+```
+
+- 示例 2:
+
+```Python
+输入:nums = [3,2,1,0,4]
+输出:false
+解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
+```
## 解题思路
-定义动态规划状态 dp[i] 为:从 0 出发,经过 j ≤ i,可以跳出的最远距离。可以得出。
+### 思路 1:贪心算法
+
+如果我们能通过前面的某个位置 $j$,到达后面的某个位置 $i$,则我们一定能到达区间 $[j, i]$ 中所有的点($j \le i$)。
-- dp[0] = nums[0]。表示从 0 出发,经过 0,可以跳出的最远距离为 nums[0]。
-- 如果能通过 0 ~ i-1 个位置到达 i,即 dp[i-1] ≥ i,则 dp[i] = max(dp[i-1], i + nums[i])。
-- 如果不能通过 0 ~ i-1 个位置到达 i,即 dp[i-1] < i,则 dp[i] = dp[i-1]。
+而前面的位置 $j$ 肯定也是通过 $j$ 前面的点到达的。所以我们可以通过贪心算法来计算出所能到达的最远位置。具体步骤如下:
-## 代码
+1. 初始化能到达的最远位置 $max_i$ 为 $0$。
+2. 遍历数组 `nums`。
+3. 如果能到达当前位置,即 $max_i \le i$,并且当前位置 + 当前位置最大跳跃长度 > 能到达的最远位置,即 $i + nums[i] > max_i$,则更新能到达的最远位置 $max_i$。
+4. 遍历完数组,最后比较能到达的最远位置 $max_i$ 和数组最远距离 `size - 1` 的关系。如果 $max_i >= len(nums)$,则返回 `True`,否则返回 `False`。
+
+### 思路 1:代码
+
+```Python
+class Solution:
+ def canJump(self, nums: List[int]) -> bool:
+ size = len(nums)
+ max_i = 0
+ for i in range(size):
+ if max_i >= i and i + nums[i] > max_i:
+ max_i = i + nums[i]
+
+ return max_i >= size - 1
+```
+
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(n)$,其中 $n$ 是数组 `nums` 的长度。
+- **空间复杂度**:
+
+### 思路 2:动态规划
+
+###### 1. 划分阶段
+
+按照位置进行阶段划分。
+
+###### 2. 定义状态
+
+定义状态 `dp[i]` 表示为:从位置 $0$ 出发,经过 $j \le i$,可以跳出的最远距离。
+
+###### 3. 状态转移方程
+
+- 如果能通过 $0 \sim i - 1$ 个位置到达 $i$,即 $dp[i-1] \le i$,则 $dp[i] = max(dp[i-1], i + nums[i])$。
+- 如果不能通过 $0 \sim i - 1$ 个位置到达 $i$,即 $dp[i - 1] < i$,则 $dp[i] = dp[i - 1]$。
+
+###### 4. 初始条件
+
+初始状态下,从 $0$ 出发,经过 $0$,可以跳出的最远距离为 `nums[0]`,即 `dp[0] = nums[0]`。
+
+###### 5. 最终结果
+
+根据我们之前定义的状态,`dp[i]` 表示为:从位置 $0$ 出发,经过 $j \le i$,可以跳出的最远距离。则我们需要判断 `dp[size - 1]` 与数组最远距离 `size - 1` 的关系。
+
+### 思路 2:代码
```Python
class Solution:
@@ -30,6 +100,11 @@ class Solution:
dp[i] = max(dp[i - 1], i + nums[i])
else:
dp[i] = dp[i - 1]
- return dp[-1] >= size - 1
+ return dp[size - 1] >= size - 1
```
+### 思路 2:复杂度分析
+
+- **时间复杂度**:$O(n)$,其中 $n$ 是数组 `nums` 的长度。
+- **空间复杂度**:$O(n)$。
+
diff --git "a/Solutions/0070. \347\210\254\346\245\274\346\242\257.md" "b/Solutions/0070. \347\210\254\346\245\274\346\242\257.md"
index 46236bcb..eadd87b5 100644
--- "a/Solutions/0070. \347\210\254\346\245\274\346\242\257.md"
+++ "b/Solutions/0070. \347\210\254\346\245\274\346\242\257.md"
@@ -38,7 +38,37 @@
## 解题思路
-### 思路 1:动态规划
+### 思路 1:递归(超时)
+
+根据我们的递推三步走策略,写出对应的递归代码。
+
+1. 写出递推公式:`f(n) = f(n - 1) + f(n - 2)`。
+2. 明确终止条件:`f(0) = 0, f(1) = 1`。
+3. 翻译为递归代码:
+ 1. 定义递归函数:`climbStairs(self, n)` 表示输入参数为问题的规模 `n`,返回结果为爬 $n$ 阶台阶到达楼顶的方案数。
+ 2. 书写递归主体:`return self.climbStairs(n - 1) + self.climbStairs(n - 2)`。
+ 3. 明确递归终止条件:
+ 1. `if n == 0: return 0`
+ 2. `if n == 1: return 1`
+
+### 思路 1:代码
+
+```Python
+class Solution:
+ def climbStairs(self, n: int) -> int:
+ if n == 1:
+ return 1
+ if n == 2:
+ return 2
+ return self.climbStairs(n - 1) + self.climbStairs(n - 2)
+```
+
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O((\frac{1 + \sqrt{5}}{2})^n)$。
+- **空间复杂度**:$O(n)$。每次递归的空间复杂度是 $O(1)$, 调用栈的深度为 $n$,所以总的空间复杂度就是 $O(n)$。
+
+### 思路 2:动态规划
###### 1. 划分阶段
@@ -62,7 +92,7 @@
根据状态定义,最终结果为 `dp[n]`,即爬到第 `n` 阶台阶(即楼顶)的方案数为 `dp[n]`。
-### 思路 1:代码
+### 思路 2:代码
```Python
class Solution:
@@ -76,7 +106,7 @@ class Solution:
return dp[n]
```
-### 思路 1:复杂度分析
+### 思路 2:复杂度分析
- **时间复杂度**:$O(n)$。一重循环遍历的时间复杂度为 $O(n)$。
- **空间复杂度**:$O(n)$。用到了一维数组保存状态,所以总体空间复杂度为 $O(n)$。因为 `dp[i]` 的状态只依赖于 `dp[i - 1]` 和 `dp[i - 2]`,所以可以使用 `3` 个变量来分别表示 `dp[i]`、`dp[i - 1]`、`dp[i - 2]`,从而将空间复杂度优化到 $O(1)$。
diff --git "a/Solutions/0079. \345\215\225\350\257\215\346\220\234\347\264\242.md" "b/Solutions/0079. \345\215\225\350\257\215\346\220\234\347\264\242.md"
index c7aad5f4..a616b6be 100644
--- "a/Solutions/0079. \345\215\225\350\257\215\346\220\234\347\264\242.md"
+++ "b/Solutions/0079. \345\215\225\350\257\215\346\220\234\347\264\242.md"
@@ -5,19 +5,54 @@
## 题目大意
-给定一个 m * n 大小的二维字符矩阵 board 和一个字符串单词 word。如果 word 存在于网格中,返回 True,否则返回 False。
+**描述**:给定一个 $m \times n$ 大小的二维字符矩阵 `board` 和一个字符串单词 `word`。
+
+**要求**:如果 `word` 存在于网格中,返回 `True`,否则返回 `False`。
+
+**说明**:
- 单词必须按照字母顺序通过上下左右相邻的单元格字母构成。且同一个单元格内的字母不允许被重复使用。
+- $m == board.length$。
+- $n == board[i].length$。
+- $1 \le m, n \le 6$。
+- $1 \le word.length \le 15$。
+- `board` 和 `word` 仅由大小写英文字母组成。
+
+**示例**:
+
+- 示例 1:
+
+
+
+```Python
+输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
+输出:true
+```
+
+- 示例 2:
+
+
+
+```Python
+输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
+输出:true
+```
## 解题思路
-回溯算法在二维矩阵 board 中按照上下左右四个方向递归搜索。设函数 `backtrack(i, j, index)` 表示从 `board[i][j]` 出发,能否搜索到单词字母 `word[index]`,以及 index 位置之后的后缀子串。如果能搜索到,则返回 True,否则返回 False。`backtrack(i, j, index)` 执行步骤如下:
+### 思路 1:回溯算法
+
+使用回溯算法在二维矩阵 `board` 中按照上下左右四个方向递归搜索。
-- 如果 $board[i][j] = word[index]$,而且 index 已经到达 word 字符串末尾,则返回 True。
-- 如果 $board[i][j] = word[index]$,而且 index 未到达 word 字符串末尾,则遍历当前位置的所有相邻位置。如果从某个相邻位置能搜索到后缀子串,则返回 True,否则返回 False。
-- 如果 $board[i][j] \ne word[index]$,则当前字符不匹配,返回 False。
+设函数 `backtrack(i, j, index)` 表示从 `board[i][j]` 出发,能否搜索到单词字母 `word[index]`,以及 `index` 位置之后的后缀子串。如果能搜索到,则返回 `True`,否则返回 `False`。
-## 代码
+`backtrack(i, j, index)` 执行步骤如下:
+
+1. 如果 $board[i][j] = word[index]$,而且 index 已经到达 word 字符串末尾,则返回 True。
+2. 如果 $board[i][j] = word[index]$,而且 index 未到达 word 字符串末尾,则遍历当前位置的所有相邻位置。如果从某个相邻位置能搜索到后缀子串,则返回 True,否则返回 False。
+3. 如果 $board[i][j] \ne word[index]$,则当前字符不匹配,返回 False。
+
+### 思路 1:代码
```Python
class Solution:
@@ -51,3 +86,8 @@ class Solution:
return False
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(m \times n \times 2^l)$,其中 $m$、$n$ 为二维矩阵 `board`的行数和列数。$l$ 为字符串 `word` 的长度。
+- **空间复杂度**:$O(m \times n)$。
+
diff --git "a/Solutions/0090. \345\255\220\351\233\206 II.md" "b/Solutions/0090. \345\255\220\351\233\206 II.md"
index d6deed23..efc75d5e 100644
--- "a/Solutions/0090. \345\255\220\351\233\206 II.md"
+++ "b/Solutions/0090. \345\255\220\351\233\206 II.md"
@@ -45,7 +45,7 @@
- 在选择该元素的情况下,继续递归考虑下一个元素。
- 进行回溯,撤销选择该元素。即从当前子集数组 `sub_set` 中移除之前添加的元素。
-### 思路 1:回溯算法代码
+### 思路 1:代码
```Python
class Solution:
@@ -66,6 +66,11 @@ class Solution:
return res
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(n \times 2^n)$,其中 $n$ 指的是数组 `nums` 的元素个数,$2^n$ 指的是所有状态数。每种状态需要 $O(n)$ 的时间来构造子集。
+- **空间复杂度**:$O(n)$,每种状态下构造子集需要使用 $O(n)$ 的空间。
+
### 思路 2:二进制枚举
对于一个元素个数为 `n` 的集合 `nums` 来说,每一个位置上的元素都有选取和未选取两种状态。我们可以用数字 `1` 来表示选取该元素,用数字 `0` 来表示不选取该元素。
@@ -103,7 +108,7 @@ class Solution:
因为数组中可能包含重复元素,所以我们可以先对数组进行排序。然后在枚举过程中,如果发现当前元素和上一个元素相同,则直接跳过当前生层的子集,从而去除重复元素。
-### 思路 2:二进制枚举代码
+### 思路 2:代码
```Python
class Solution:
@@ -124,3 +129,8 @@ class Solution:
sub_sets.append(sub_set) # 将子集 sub_set 加入到所有子集数组 sub_sets 中
return sub_sets # 返回所有子集
```
+
+### 思路 2:复杂度分析
+
+- **时间复杂度**:$O(n \times 2^n)$,其中 $n$ 指的是数组 `nums` 的元素个数,$2^n$ 指的是所有状态数。每种状态需要 $O(n)$ 的时间来构造子集。
+- **空间复杂度**:$O(n)$,每种状态下构造子集需要使用 $O(n)$ 的空间。
diff --git "a/Solutions/0092. \345\217\215\350\275\254\351\223\276\350\241\250 II.md" "b/Solutions/0092. \345\217\215\350\275\254\351\223\276\350\241\250 II.md"
index 873743ff..2081128e 100644
--- "a/Solutions/0092. \345\217\215\350\275\254\351\223\276\350\241\250 II.md"
+++ "b/Solutions/0092. \345\217\215\350\275\254\351\223\276\350\241\250 II.md"
@@ -27,9 +27,11 @@
## 解题思路
+在「[0206. 反转链表](https://leetcode.cn/problems/reverse-linked-list/)」中我们可以通过迭代、递归两种方法将整个链表反转。这道题而这道题要求对链表的部分区间进行反转。我们同样可以通过迭代、递归两种方法将链表的部分区间进行反转。
+
### 思路 1:迭代
-在「[0206. 反转链表](https://leetcode.cn/problems/reverse-linked-list/)」中我们可以通过迭代、递归两种方法将整个链表反转。而这道题要求对链表的部分区间进行反转。我们可以先遍历到需要反转的链表区间的前一个节点,然后对需要反转的链表区间进行迭代反转。最后再返回头节点即可。
+我们可以先遍历到需要反转的链表区间的前一个节点,然后对需要反转的链表区间进行迭代反转。最后再返回头节点即可。
但是需要注意一点,如果需要反转的区间包含了链表的第一个节点,那么我们可以事先创建一个哑节点作为链表初始位置开始遍历,这样就能避免找不到需要反转的链表区间的前一个节点。
@@ -48,7 +50,7 @@
6. 最后等到 `cur` 遍历到链表末尾(即 `cur == None`)或者遍历到需要反转区间的末尾时(即 `index > right`) 时,将反转区间的头尾节点分别与之前保存的需要反转的区间的前一个节点 `reverse_start` 相连,即 `reverse_start.next.next = cur`,`reverse_start.next = pre`。
7. 最后返回新的头节点 `dummy_head.next`。
-### 思路 1:迭代代码
+### 思路 1:代码
```Python
# Definition for singly-linked list.
@@ -88,6 +90,54 @@ class Solution:
- **时间复杂度**:$O(n)$。其中 $n$ 是链表节点个数。
- **空间复杂度**:$O(1)$。
+### 思路 2:递归算法
+
+#### 1. 翻转链表前 n 个节点
+
+1. 当 `left == 1` 时,无论 `right` 等于多少,实际上都是将当前链表到 `right` 部分进行翻转,也就是将前 `right` 个节点进行翻转。
+
+2. 我们可以先定义一个递归函数 `reverseN(self, head, n)`,含义为:将链表前第 $n$ 个节点位置进行翻转。
+ 1. 然后从 `head.next` 的位置开始调用递归函数,即将 `head.next` 为头节点的链表的的前 $n - 1$ 个位置进行反转,并返回该链表的新头节点 `new_head`。
+ 2. 然后改变 `head`(原先头节点)和 `new_head`(新头节点)之间的指向关系,即将 `head` 指向的节点作为 `head` 下一个节点的下一个节点。
+ 3. 先保存 `head.next` 的 `next` 指针,也就是新链表前 $n$ 个节点的尾指针,即 `last = head.next.next`。
+ 4. 将 `head.next` 的`next` 指针先指向当前节点 `head`,即 `head.next.next = head `。
+ 5. 然后让当前节点 `head` 的 `next` 指针指向 `last`,则完成了前 $n - 1$ 个位置的翻转。
+
+3. 递归终止条件:当 `n == 1` 时,相当于翻转第一个节点,直接返回 `head` 即可。
+
+4. #### 翻转链表 `[left, right]` 上的节点。
+
+接下来我们来翻转区间上的节点。
+
+1. 定义递归函数 `reverseBetween(self, head, left, right)` 为
+2.
+
+### 思路 2:代码
+
+```Python
+class Solution:
+ def reverseBetween(self, head: Optional[ListNode], left: int, right: int) -> Optional[ListNode]:
+ if left == 1:
+ return self.reverseN(head, right)
+
+ head.next = self.reverseBetween(head.next, left - 1, right - 1)
+ return head
+
+ def reverseN(self, head, n):
+ if n == 1:
+ return head
+ last = self.reverseN(head.next, n - 1)
+ next = head.next.next
+ head.next.next = head
+ head.next = next
+ return last
+```
+
+### 思路 2:复杂度分析
+
+- **时间复杂度**:$O(n)$。
+- **空间复杂度**:$O(n)$。最多需要 $n$ 层栈空间。
+
## 参考资料
- 【题解】[动画图解:翻转链表的指定区间 - 反转链表 II - 力扣](https://leetcode.cn/problems/reverse-linked-list-ii/solution/dong-hua-tu-jie-fan-zhuan-lian-biao-de-z-n4px/)
diff --git "a/Solutions/0135. \345\210\206\345\217\221\347\263\226\346\236\234.md" "b/Solutions/0135. \345\210\206\345\217\221\347\263\226\346\236\234.md"
index bfe72227..246f54a5 100644
--- "a/Solutions/0135. \345\210\206\345\217\221\347\263\226\346\236\234.md"
+++ "b/Solutions/0135. \345\210\206\345\217\221\347\263\226\346\236\234.md"
@@ -5,31 +5,60 @@
## 题目大意
-N 个孩子站成一排。老师会根据每个孩子的表现,给每个孩子进行评分。然后根据下面的规则给孩子们分发糖果:
+**描述**:$n$ 个孩子站成一排。老师会根据每个孩子的表现,给每个孩子进行评分。然后根据下面的规则给孩子们分发糖果:
-- 每个孩子至少得 1 个糖果。
+- 每个孩子至少得 $1$ 个糖果。
- 评分更高的孩子必须比他两侧相邻位置上的孩子分得更多的糖果。
-现在给定 N 个孩子的表现分数数组 ratings,要求返回最少需要准备的糖果数目。
+现在给定 $n$ 个孩子的表现分数数组 `ratings`,其中 `ratings[i]` 表示第 $i$ 个孩子的评分。
+
+**要求**:返回最少需要准备的糖果数目。
+
+**说明**:
+
+- $n == ratings.length$。
+- $1 \le n \le 2 \times 10^4$。
+- $0 \le ratings[i] \le 2 * 10^4$。
+
+**示例**:
+
+- 示例 1:
+
+```Python
+输入:ratings = [1,0,2]
+输出:5
+解释:你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。
+```
+
+- 示例 2:
+
+```Python
+输入:ratings = [1,2,2]
+输出:4
+解释:你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
+ 第三个孩子只得到 1 颗糖果,这满足题面中的两个条件。
+```
## 解题思路
+### 思路 1:贪心算法
+
先来看分发糖果的规则。
「每个孩子至少得 1 个糖果」:说明糖果数目至少为 N 个。
「评分更高的孩子必须比他两侧相邻位置上的孩子分得更多的糖果」:可以看做为以下两种条件:
-- 当 `ratings[i - 1] < ratings[i]` 时,第 i 个孩子的糖果数量比第 i - 1 个孩子的糖果数量多;
-- 当 `ratings[i] > ratings[i + 1]` 时,第 i 个孩子的糖果数量比第 i + 1 个孩子的糖果数量多。
+- 当 $ratings[i - 1] < ratings[i]$ 时,第 i 个孩子的糖果数量比第 $i - 1$ 个孩子的糖果数量多;
+- 当 $ratings[i] > ratings[i + 1]$ 时,第 i 个孩子的糖果数量比第$ i + 1$ 个孩子的糖果数量多。
根据以上信息,我们可以设定一个长度为 N 的数组 sweets 来表示每个孩子分得的最少糖果数,初始每个孩子分得糖果数都为 1。
-然后遍历两遍数组,第一遍遍历满足当 `ratings[i - 1] < ratings[i]` 时,第 i 个孩子的糖果数量比第 i - 1 个孩子的糖果数量多 1 个。第二遍遍历满足当 `ratings[i] > ratings[i + 1]` 时,第 i 个孩子的糖果数量取「第 i + 1 个孩子的糖果数量多 1个」和「第 i + 1 个孩子目前拥有的糖果数量」中的最大值。
+然后遍历两遍数组,第一遍遍历满足当 $ratings[i - 1] < ratings[i]$ 时,第 $i$ 个孩子的糖果数量比第 $i - 1$ 个孩子的糖果数量多 $1$ 个。第二遍遍历满足当 $ratings[i] > ratings[i + 1]$ 时,第 $i$ 个孩子的糖果数量取「第 $i + 1$ 个孩子的糖果数量多 $1$ 个」和「第 $i + 1$ 个孩子目前拥有的糖果数量」中的最大值。
然后再遍历求所有孩子的糖果数量和即为答案。
-## 代码
+### 思路 1:代码
```Python
class Solution:
@@ -49,3 +78,8 @@ class Solution:
return res
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(n)$,其中 $n$ 是数组 `ratings` 的长度。
+- **空间复杂度**:$O(n)$。
+
diff --git "a/Solutions/0169. \345\244\232\346\225\260\345\205\203\347\264\240.md" "b/Solutions/0169. \345\244\232\346\225\260\345\205\203\347\264\240.md"
index 21c09637..7b79528a 100644
--- "a/Solutions/0169. \345\244\232\346\225\260\345\205\203\347\264\240.md"
+++ "b/Solutions/0169. \345\244\232\346\225\260\345\205\203\347\264\240.md"
@@ -62,4 +62,53 @@ class Solution:
### 思路 1:复杂度分析
- **时间复杂度**:$O(n)$。
-- **空间复杂度**:$O(n)$。
\ No newline at end of file
+- **空间复杂度**:$O(n)$。
+
+### 思路 2:分治算法
+
+如果 `num` 是数组 `nums` 的众数,那么我们将 `nums` 分为两部分,则 `num` 至少是其中一部分的众数。
+
+则我们可以用分治法来解决这个问题。具体步骤如下:
+
+1. 将数组 `nums` 递归地将当前序列平均分成左右两个数组,直到所有子数组长度为 `1`。
+2. 长度为 $1$ 的子数组众数肯定是数组中唯一的数,将其返回即可。
+3. 将两个子数组依次向上两两合并。
+ 1. 如果两个子数组的众数相同,则说明合并后的数组众数为:两个子数组的众数。
+ 2. 如果两个子数组的众数不同,则需要比较两个众数在整个区间的众数。
+
+4. 最后返回整个数组的众数。
+
+### 思路 2:代码
+
+```Python
+class Solution:
+ def majorityElement(self, nums: List[int]) -> int:
+ def get_mode(low, high):
+ if low == high:
+ return nums[low]
+
+ mid = low + (high - low) // 2
+ left_mod = get_mode(low, mid)
+ right_mod = get_mode(mid + 1, high)
+
+ if left_mod == right_mod:
+ return left_mod
+
+ left_mod_cnt, right_mod_cnt = 0, 0
+ for i in range(low, high + 1):
+ if nums[i] == left_mod:
+ left_mod_cnt += 1
+ if nums[i] == right_mod:
+ right_mod_cnt += 1
+
+ if left_mod_cnt > right_mod_cnt:
+ return left_mod
+ return right_mod
+
+ return get_mode(0, len(nums) - 1)
+```
+
+### 思路 2:复杂度分析
+
+- **时间复杂度**:$O(n \times \log n)$。
+- **空间复杂度**:$O(\log n)$。
\ No newline at end of file
diff --git "a/Solutions/0204. \350\256\241\346\225\260\350\264\250\346\225\260.md" "b/Solutions/0204. \350\256\241\346\225\260\350\264\250\346\225\260.md"
index e9c5d6ff..fae2b5a3 100644
--- "a/Solutions/0204. \350\256\241\346\225\260\350\264\250\346\225\260.md"
+++ "b/Solutions/0204. \350\256\241\346\225\260\350\264\250\346\225\260.md"
@@ -1,13 +1,17 @@
# [0204. 计数质数](https://leetcode.cn/problems/count-primes/)
-- 标签:数学、哈希表
+- 标签:数组、数学、枚举、数论
- 难度:简单
## 题目大意
-**描述**:给定 一个非负整数 `n`。
+**描述**:给定 一个非负整数 $n$。
-**要求**:统计小于 `n` 的质数数量。
+**要求**:统计小于 $n$ 的质数数量。
+
+**说明**:
+
+- $0 \le n \le 5 * 10^6$。
**示例**:
@@ -16,24 +20,31 @@
```Python
输入 n = 10
输出 4
-解释 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
+解释 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7。
+```
+
+- 示例 2:
+
+```Python
+输入:n = 1
+输出:0
```
## 解题思路
### 思路 1:枚举算法(超时)
-对于小于 `n` 的每一个数 `x`,我们可以枚举区间 `[2, x - 1]` 上的数是否是 `x` 的因数,即是否存在能被 `x` 整数的数。如果存在,则该数 `x` 不是质数。如果不存在,则该数 `x` 是质数。
+对于小于 $n$ 的每一个数 $x$,我们可以枚举区间 $[2, x - 1]$ 上的数是否是 $x$ 的因数,即是否存在能被 $x$ 整数的数。如果存在,则该数 $x$ 不是质数。如果不存在,则该数 $x$ 是质数。
-这样我们就可以通过枚举 `[2, n - 1]` 上的所有数 `x`,并判断 `x` 是否为质数。
+这样我们就可以通过枚举 $[2, n - 1]$ 上的所有数 $x$,并判断 $x$ 是否为质数。
-在遍历枚举的同时,我们维护一个用于统计小于 `n` 的质数数量的变量 `cnt`。如果符合要求,则将计数 `cnt` 加 `1`。最终返回该数目作为答案。
+在遍历枚举的同时,我们维护一个用于统计小于 $n$ 的质数数量的变量 `cnt`。如果符合要求,则将计数 `cnt` 加 $1$。最终返回该数目作为答案。
-考虑到如果 `i` 是 `x` 的因数,则 $\frac{x}{i}$ 也必然是 `x` 的因数,则我们只需要检验这两个因数中的较小数即可。而较小数一定会落在 $[2, \sqrt x]$ 上。因此我们在检验 `x` 是否为质数时,只需要枚举 $[2, \sqrt x]$ 中的所有数即可。
+考虑到如果 $i$ 是 $x$ 的因数,则 $\frac{x}{i}$ 也必然是 $x$ 的因数,则我们只需要检验这两个因数中的较小数即可。而较小数一定会落在 $[2, \sqrt x]$ 上。因此我们在检验 $x$ 是否为质数时,只需要枚举 $[2, \sqrt x]$ 中的所有数即可。
-利用枚举算法单次检查单个数的时间复杂度为 $O(\sqrt{n})$,检查 `n` 个数的整体时间复杂度为 $O(n \sqrt{n})$。
+利用枚举算法单次检查单个数的时间复杂度为 $O(\sqrt{n})$,检查 $n$ 个数的整体时间复杂度为 $O(n \sqrt{n})$。
-### 思路 1:枚举算法代码(超时)
+### 思路 1:代码
```Python
class Solution:
@@ -51,18 +62,23 @@ class Solution:
return cnt
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(n \times \sqrt{n})$。
+- **空间复杂度**:$O(1)$。
+
### 思路 2:埃氏筛法
可以用「埃氏筛」进行求解。这种方法是由古希腊数学家埃拉托斯尼斯提出的,具体步骤如下:
-- 使用长度为 `n` 的数组 `is_prime` 来判断一个数是否是质数。如果 `is_prime[i] == True` ,则表示 `i` 是质数,如果 `is_prime[i] == False`,则表示 `i` 不是质数。并使用变量 `count` 标记质数个数。
-- 然后从 `[2, n - 1]` 的第一个质数(即数字 `2`) 开始,令 `count` 加 `1`,并将该质数在 `[2, n - 1]` 范围内所有倍数(即 `4`、`6`、`8`、...)都标记为非质数。
-- 然后根据数组 `is_prime` 中的信息,找到下一个没有标记为非质数的质数(即数字 `3`),令 `count` 加 `1`,然后将该质数在 `2, n - 1]` 范围内的所有倍数(即 `6`、`9`、`12`、…)都标记为非质数。
-- 以此类推,直到所有小于或等于 `n - 1` 的质数和质数的倍数都标记完毕时,输出 `count`。
+- 使用长度为 $n$ 的数组 `is_prime` 来判断一个数是否是质数。如果 `is_prime[i] == True` ,则表示 $i$ 是质数,如果 `is_prime[i] == False`,则表示 $i$ 不是质数。并使用变量 `count` 标记质数个数。
+- 然后从 $[2, n - 1]$ 的第一个质数(即数字 $2$) 开始,令 `count` 加 $1$,并将该质数在 $[2, n - 1]$ 范围内所有倍数(即 $4$、$6$、$8$、...)都标记为非质数。
+- 然后根据数组 `is_prime` 中的信息,找到下一个没有标记为非质数的质数(即数字 $3$),令 `count` 加 $1$,然后将该质数在 $[2, n - 1]$ 范围内的所有倍数(即 $6$、$9$、$12$、…)都标记为非质数。
+- 以此类推,直到所有小于或等于 $n - 1$ 的质数和质数的倍数都标记完毕时,输出 `count`。
-优化:对于一个质数 `x`,我们可以直接从 `x * x` 开始标记,这是因为 `2 * x`、`3 * x`、… 这些数已经在 `x` 之前就被其他数的倍数标记过了,例如 `2` 的所有倍数、`3` 的所有倍数等等。
+优化:对于一个质数 $x$,我们可以直接从 $x \times x$ 开始标记,这是因为 $2 \times x$、$3 \times x$、… 这些数已经在 $x$ 之前就被其他数的倍数标记过了,例如 $2$ 的所有倍数、$3$ 的所有倍数等等。
-### 思路 2:埃氏筛法代码
+### 思路 2:代码
```Python
class Solution:
@@ -77,3 +93,8 @@ class Solution:
return count
```
+### 思路 2:复杂度分析
+
+- **时间复杂度**:$O(n \times \log_2{log_2n})$。
+- **空间复杂度**:$O(n)$。
+
diff --git "a/Solutions/0226. \347\277\273\350\275\254\344\272\214\345\217\211\346\240\221.md" "b/Solutions/0226. \347\277\273\350\275\254\344\272\214\345\217\211\346\240\221.md"
index 70d1d032..01209f23 100644
--- "a/Solutions/0226. \347\277\273\350\275\254\344\272\214\345\217\211\346\240\221.md"
+++ "b/Solutions/0226. \347\277\273\350\275\254\344\272\214\345\217\211\346\240\221.md"
@@ -38,11 +38,32 @@
### 思路 1:递归遍历
-1. 从根节点 `root` 开始遍历,如果根节点为 `None`,直接返回 `None`。
-2. 递归遍历左子树。
-3. 递归遍历右子树。
-4. 从叶子节点向上递归交换左右子树位置。
-5. 返回根节点 `root`。
+根据我们的递推三步走策略,写出对应的递归代码。
+
+1. 写出递推公式:
+
+ 1. 递归遍历翻转左子树。
+ 2. 递归遍历翻转右子树。
+ 3. 交换当前根节点 `root` 的左右子树。
+
+2. 明确终止条件:当前节点 `root` 为 `None`。
+
+3. 翻译为递归代码:
+ 1. 定义递归函数:`invertTree(self, root)` 表示输入参数为二叉树的根节点 `root`,返回结果为翻转后二叉树的根节点。
+
+ 2. 书写递归主体:
+
+ ```Python
+ left = self.invertTree(root.left)
+ right = self.invertTree(root.right)
+ root.left = right
+ root.right = left
+ return root
+ ```
+
+ 3. 明确递归终止条件:`if not root: return None`
+
+4. 返回根节点 `root`。
### 思路 1:代码
diff --git "a/Solutions/0435. \346\227\240\351\207\215\345\217\240\345\214\272\351\227\264.md" "b/Solutions/0435. \346\227\240\351\207\215\345\217\240\345\214\272\351\227\264.md"
index e9823584..c95eab67 100644
--- "a/Solutions/0435. \346\227\240\351\207\215\345\217\240\345\214\272\351\227\264.md"
+++ "b/Solutions/0435. \346\227\240\351\207\215\345\217\240\345\214\272\351\227\264.md"
@@ -25,11 +25,19 @@
解释:移除 [1,3] 后,剩下的区间没有重叠。
```
+- 示例 2:
+
+```Python
+输入: intervals = [ [1,2], [1,2], [1,2] ]
+输出: 2
+解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
+```
+
## 解题思路
### 思路 1:贪心算法
-这道题我们可以转换一下思路。原题要求保证移除区间最少,使得剩下的区间互不重叠。换个角度就是:「如何使得剩下互补重叠区间的数目最多」。那么答案就变为了:「总区间个数 - 不重叠区间的最多个数」。我们的问题也变成了求所有区间中不重叠区间的最多个数。
+这道题我们可以转换一下思路。原题要求保证移除区间最少,使得剩下的区间互不重叠。换个角度就是:「如何使得剩下互不重叠区间的数目最多」。那么答案就变为了:「总区间个数 - 不重叠区间的最多个数」。我们的问题也变成了求所有区间中不重叠区间的最多个数。
从贪心算法的角度来考虑,我们应该将区间按照结束时间排序。每次选择结束时间最早的区间,然后再在剩下的时间内选出最多的区间。
@@ -46,7 +54,7 @@
1. 如果 `end_pos <= intervals[i][0]`,即 `end_pos` 小于等于区间起始位置,则说明出现了不重叠区间,令不重叠区间数 `count` 加 `1`,`end_pos` 更新为新区间的结束位置。
3. 最终返回「总区间个数 - 不重叠区间的最多个数」即 `len(intervals) - count` 作为答案。
-### 思路 1:贪心算法代码
+### 思路 1:代码
```Python
class Solution:
@@ -64,3 +72,7 @@ class Solution:
return len(intervals) - count
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(n \times \log n)$,其中 $n$ 是区间的数量。
+- **空间复杂度**:$O(\log n)$。
diff --git "a/Solutions/0452. \347\224\250\346\234\200\345\260\221\346\225\260\351\207\217\347\232\204\347\256\255\345\274\225\347\210\206\346\260\224\347\220\203.md" "b/Solutions/0452. \347\224\250\346\234\200\345\260\221\346\225\260\351\207\217\347\232\204\347\256\255\345\274\225\347\210\206\346\260\224\347\220\203.md"
index 500e3784..bb92efad 100644
--- "a/Solutions/0452. \347\224\250\346\234\200\345\260\221\346\225\260\351\207\217\347\232\204\347\256\255\345\274\225\347\210\206\346\260\224\347\220\203.md"
+++ "b/Solutions/0452. \347\224\250\346\234\200\345\260\221\346\225\260\351\207\217\347\232\204\347\256\255\345\274\225\347\210\206\346\260\224\347\220\203.md"
@@ -5,31 +5,61 @@
## 题目大意
-在一个坐标系中有许多球形的气球。对于每个气球,给定气球在 x 轴上的开始坐标和结束坐标 $(x_{start}, x_{end})$。
+**描述**:在一个坐标系中有许多球形的气球。对于每个气球,给定气球在 x 轴上的开始坐标和结束坐标 $(x_{start}, x_{end})$。
-同时,在 x 轴的任意位置都能垂直发出弓箭,假设弓箭发出的坐标就是 x。那么如果有气球满足 $x_{start} \le x \le x_{end}$,则该气球就会被引爆,且弓箭可以无限前进,可以将满足上述要求的气球全部引爆。
+同时,在 $x$ 轴的任意位置都能垂直发出弓箭,假设弓箭发出的坐标就是 x。那么如果有气球满足 $x_{start} \le x \le x_{end}$,则该气球就会被引爆,且弓箭可以无限前进,可以将满足上述要求的气球全部引爆。
-现在给定一个数组 points ,`points[i] = [x_{start}, x_{end}]` 代表每个气球的开始坐标和结束坐标。返回能引爆所有气球的最小弓箭数。
+现在给定一个数组 `points`,其中 $points[i] = [x_{start}, x_{end}]$ 代表每个气球的开始坐标和结束坐标。
+
+**要求**:返回能引爆所有气球的最小弓箭数。
+
+**说明**:
+
+- $1 \le points.length \le 10^5$。
+- $points[i].length == 2$。
+- $-2^{31} \le x_{start} < x_{end} \le 2^{31} - 1$。
+
+**示例**:
+
+- 示例 1:
+
+```Python
+输入:points = [[10,16],[2,8],[1,6],[7,12]]
+输出:2
+解释:气球可以用 2 支箭来爆破:
+- 在x = 6 处射出箭,击破气球 [2,8] 和 [1,6]。
+- 在x = 11 处发射箭,击破气球 [10,16] 和 [7,12]。
+```
+
+- 示例 2:
+
+```Python
+输入:points = [[1,2],[3,4],[5,6],[7,8]]
+输出:4
+解释:每个气球需要射出一支箭,总共需要 4 支箭。
+```
## 解题思路
+### 思路 1:贪心算法
+
弓箭的起始位置和结束位置可以看做是一段区间,直观上来看,为了使用最少的弓箭数,可以尽量射中区间重叠最多的地方。
所以问题变为了:**如何寻找区间重叠最多的地方,也就是区间交集最多的地方。**
-我们将 points 按结束坐标升序排序(为什么按照结束坐标排序后边说)。
+我们将 `points` 按结束坐标升序排序(为什么按照结束坐标排序后边说)。
-然后维护两个变量:一个是当前弓箭的坐标 arrow_pos、另一个是弓箭的数目 count。
+然后维护两个变量:一个是当前弓箭的坐标 `arrow_pos`、另一个是弓箭的数目 `count`。
为了尽可能的穿过更多的区间,所以每一支弓箭都应该尽可能的从区间的结束位置穿过,这样才能覆盖更多的区间。
-初始情况下,第一支弓箭的坐标为第一个区间的结束位置,然后弓箭数为 1。然后依次遍历每段区间。
+初始情况下,第一支弓箭的坐标为第一个区间的结束位置,然后弓箭数为 $1$。然后依次遍历每段区间。
-如果遇到弓箭坐标小于区间起始位置的情况,说明该弓箭不能引爆该区间对应的气球,需要用新的弓箭来射,所以弓箭数 + 1,弓箭坐标也需要更新为新区间的结束位置。
+如果遇到弓箭坐标小于区间起始位置的情况,说明该弓箭不能引爆该区间对应的气球,需要用新的弓箭来射,所以弓箭数加 $1$,弓箭坐标也需要更新为新区间的结束位置。
最终返回弓箭数目。
-再来看为什么将 points 按结束坐标升序排序而不是按照开始坐标升序排序?
+再来看为什么将 `points` 按结束坐标升序排序而不是按照开始坐标升序排序?
其实也可以,但是按开始坐标排序不如按结束坐标排序简单。
@@ -45,7 +75,7 @@
而按照结束坐标排序的话,箭的位置一开始就确定了,不需要再改变和判断箭的位置,直接判断区间即可。
-## 代码
+### 思路 1:代码
1. 按照结束位置升序排序
@@ -83,3 +113,8 @@ class Solution:
return count
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(n \times \log n)$, 其中 $n$ 是数组 `points` 的长度。
+- **空间复杂度**:$O(\log n)$。
+
diff --git "a/Solutions/0455. \345\210\206\345\217\221\351\245\274\345\271\262.md" "b/Solutions/0455. \345\210\206\345\217\221\351\245\274\345\271\262.md"
index 97b2afb1..a0a4c1f8 100644
--- "a/Solutions/0455. \345\210\206\345\217\221\351\245\274\345\271\262.md"
+++ "b/Solutions/0455. \345\210\206\345\217\221\351\245\274\345\271\262.md"
@@ -27,6 +27,14 @@
解释:你有三个孩子和两块小饼干,3 个孩子的胃口值分别是:1, 2, 3。虽然你有两块小饼干,由于他们的尺寸都是 1,你只能让胃口值是 1 的孩子满足。所以应该输出 1。
```
+- 示例 2:
+
+```Python
+输入: g = [1,2], s = [1,2,3]
+输出: 2
+解释: 你有两个孩子和三块小饼干,2个孩子的胃口值分别是1, 2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出 2。
+```
+
## 解题思路
### 思路 1:贪心算法
@@ -49,8 +57,7 @@
2. 如果 `g[index_g] > s[index_s]`,说明当前饼干无法满足当前孩子胃口,则向右移动 `index_s`,判断下一块饼干是否可以满足当前孩子胃口。
3. 遍历完输出答案 `res`。
-
-### 思路 1:贪心算法代码
+### 思路 1:代码
```Python
class Solution:
@@ -70,3 +77,7 @@ class Solution:
return res
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(m \times \log m + n \times \log n)$,其中 $m$ 和 $n$ 分别是数组 $g$ 和 $s$ 的长度。
+- **空间复杂度**:$O(\log m + \log n)$。
diff --git "a/Solutions/0509. \346\226\220\346\263\242\351\202\243\345\245\221\346\225\260.md" "b/Solutions/0509. \346\226\220\346\263\242\351\202\243\345\245\221\346\225\260.md"
index 5581fdaf..79b2c4fa 100644
--- "a/Solutions/0509. \346\226\220\346\263\242\351\202\243\345\245\221\346\225\260.md"
+++ "b/Solutions/0509. \346\226\220\346\263\242\351\202\243\345\245\221\346\225\260.md"
@@ -5,15 +5,16 @@
## 题目大意
-**描述**:给定一个整数 `n`。
+**描述**:给定一个整数 $n$。
-**要求**:计算第 `n` 个斐波那契数。
+**要求**:计算第 $n$ 个斐波那契数。
**说明**:
- 斐波那契数列的定义如下:
- - `f(0) = 0, f(1) = 1`。
- - `f(n) = f(n - 1) + f(n - 2)`,其中 `n > 1`。
+ - $f(0) = 0, f(1) = 1$。
+ - $f(n) = f(n - 1) + f(n - 2)$,其中 $n > 1$。
+- $0 \le n \le 30$。
**示例**:
@@ -25,6 +26,14 @@
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
```
+- 示例 2:
+
+```Python
+输入:n = 3
+输出:2
+解释:F(3) = F(2) + F(1) = 1 + 1 = 2
+```
+
## 解题思路
### 思路 1:递归算法
@@ -40,7 +49,7 @@
1. `if n == 0: return 0`
2. `if n == 1: return 1`
-### 思路 1:递归算法代码
+### 思路 1:代码
```Python
class Solution:
@@ -52,7 +61,7 @@ class Solution:
return self.fib(n - 1) + self.fib(n - 2)
```
-### 思路 2:复杂度分析
+### 思路 1:复杂度分析
- **时间复杂度**:$O((\frac{1 + \sqrt{5}}{2})^n)$。具体证明方法参考 [递归求斐波那契数列的时间复杂度,不要被网上的答案误导了 - 知乎](https://zhuanlan.zhihu.com/p/256344121)。
- **空间复杂度**:$O(n)$。每次递归的空间复杂度是 $O(1)$, 调用栈的深度为 $n$,所以总的空间复杂度就是 $O(n)$。
@@ -79,7 +88,7 @@ class Solution:
根据状态定义,最终结果为 `dp[n]`,即第 `n` 个斐波那契数为 `dp[n]`。
-### 思路 2:动态规划代码
+### 思路 2:代码
```Python
class Solution:
diff --git "a/Solutions/0779. \347\254\254K\344\270\252\350\257\255\346\263\225\347\254\246\345\217\267.md" "b/Solutions/0779. \347\254\254K\344\270\252\350\257\255\346\263\225\347\254\246\345\217\267.md"
index 5e8d0f0e..c7400904 100644
--- "a/Solutions/0779. \347\254\254K\344\270\252\350\257\255\346\263\225\347\254\246\345\217\267.md"
+++ "b/Solutions/0779. \347\254\254K\344\270\252\350\257\255\346\263\225\347\254\246\345\217\267.md"
@@ -5,32 +5,56 @@
## 题目大意
-给定两个整数 n 和 k,按照下面的规则来生成字符串:
+**描述**:给定两个整数 $n$ 和 $k$。我们可以按照下面的规则来生成字符串:
-- 第一行写上一个 `0`。
-- 从第二行开始,每一行将上一行的 `0` 替换成 `01`,`1` 替换为 `10`。
+- 第一行写上一个 $0$。
+- 从第二行开始,每一行将上一行的 $0$ 替换成 $01$,$1$ 替换为 $10$。
+**要求**:输出第 $n$ 行字符串中的第 $k$ 个字符。
+
+**说明**:
+
+- $1 \le n \le 30$。
+- $1 \le k \le 2^{n - 1}$。
+
+**示例**:
+
+- 示例 1:
+
+```Python
+输入: n = 2, k = 1
+输出: 0
+解释:
+第一行: 0
+第二行: 01
```
+
+- 示例 2:
+
+```Python
+输入: n = 4, k = 4
+输出: 0
+解释:
第一行:0
第二行:01
第三行:0110
第四行:01101001
```
-要求:输出第 n 行字符串中的第 k 个字符。
-
## 解题思路
-每一行都是由上一行生成的。将多行写到一起找下规律。
+### 思路 1:递归算法 + 找规律
-可以发现:第 k 个数字是由上一位对应位置上的数字生成的。
+每一行都是由上一行生成的。我们可以将多行写到一起找下规律。
-- k 在奇数位时,由上一行 (k + 1) / 2 位置的值生成。且与上一行 (k + 1) / 2 位置的值相同;
-- k 在偶数位时,由上一行 k / 2 位置的值生成。且与上一行 k / 2 位置的值相反。
+可以发现:第 $k$ 个数字是由上一位对应位置上的数字生成的。
+
+- $k$ 在奇数位时,由上一行 $(k + 1) / 2$ 位置的值生成。且与上一行 $(k + 1) / 2$ 位置的值相同;
+- $k$ 在偶数位时,由上一行 $k / 2$ 位置的值生成。且与上一行 $k / 2$ 位置的值相反。
接下来就是递归求解即可。
-## 代码
+### 思路 1:代码
```Python
class Solution:
@@ -38,8 +62,13 @@ class Solution:
if n == 0:
return 0
if k % 2 == 1:
- return self.kthGrammar(n-1, (k+1) // 2)
+ return self.kthGrammar(n - 1, (k + 1) // 2)
else:
- return abs(self.kthGrammar(n-1, k // 2) - 1)
+ return abs(self.kthGrammar(n - 1, k // 2) - 1)
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(n)$。
+- **空间复杂度**:$O(n)$。
+
diff --git "a/Solutions/0860. \346\237\240\346\252\254\346\260\264\346\211\276\351\233\266.md" "b/Solutions/0860. \346\237\240\346\252\254\346\260\264\346\211\276\351\233\266.md"
index 104412c0..b67e9338 100644
--- "a/Solutions/0860. \346\237\240\346\252\254\346\260\264\346\211\276\351\233\266.md"
+++ "b/Solutions/0860. \346\237\240\346\252\254\346\260\264\346\211\276\351\233\266.md"
@@ -5,23 +5,57 @@
## 题目大意
-一杯柠檬水的售价是 5 美元。现在有 N 个顾客排队购买柠檬水,每人只能购买一杯。顾客支付的钱面额有 5 美元、10 美元、20 美元。必须给每个顾客正确找零(就是每位顾客需要向你支付 5 美元,多出的钱要找还回顾客)。
+**描述**:一杯柠檬水的售价是 $5$ 美元。现在有 $n$ 个顾客排队购买柠檬水,每人只能购买一杯。顾客支付的钱面额有 $5$ 美元、$10$ 美元、$20$ 美元。必须给每个顾客正确找零(就是每位顾客需要向你支付 $5$ 美元,多出的钱要找还回顾客)。
-现在给定 N 个顾客支付的钱币面额数组 bills,如果能给每位顾客正确找零,则返回 True,否则返回 False。
+现在给定 $n$ 个顾客支付的钱币面额数组 `bills`。
-注意:一开始的时候手头没有任何零钱。
+**要求**:如果能给每位顾客正确找零,则返回 `True`,否则返回 `False`。
+
+**说明**:
+
+- 一开始的时候手头没有任何零钱。
+- $1 \le bills.length \le 10^5$。
+- `bills[i]` 不是 $5$ 就是 $10$ 或是 $20$。
+
+**示例**:
+
+- 示例 1:
+
+```Python
+输入:bills = [5,5,5,10,20]
+输出:True
+解释:
+前 3 位顾客那里,我们按顺序收取 3 张 5 美元的钞票。
+第 4 位顾客那里,我们收取一张 10 美元的钞票,并返还 5 美元。
+第 5 位顾客那里,我们找还一张 10 美元的钞票和一张 5 美元的钞票。
+由于所有客户都得到了正确的找零,所以我们输出 True。
+```
+
+- 示例 2:
+
+```Python
+输入:bills = [5,5,10,10,20]
+输出:False
+解释:
+前 2 位顾客那里,我们按顺序收取 2 张 5 美元的钞票。
+对于接下来的 2 位顾客,我们收取一张 10 美元的钞票,然后返还 5 美元。
+对于最后一位顾客,我们无法退回 15 美元,因为我们现在只有两张 10 美元的钞票。
+由于不是每位顾客都得到了正确的找零,所以答案是 False。
+```
## 解题思路
-由于顾客只能给我们 5、10、20 三种面额的钞票,且一开始我们手头没有任何钞票,所以我们手中所能拥有的钞票面额只能是 5、10、20。因此可以采取下面的策略。
+### 思路 1:贪心算法
-- 如果顾客支付 5 美元,直接收下。
-- 如果顾客支付 10 美元,如果我们手头有 5 美元面额的钞票,则找给顾客,否则无法正确找零,返回 False。
-- 如果顾客支付 20 美元,如果我们手头有 1 张 10 美元和 1 张 5 美元的钞票,或者有 3 张 5 美元的钞票,则可以找给顾客。如果两种组合方式同时存在,倾向于第 1 种方式找零,因为使用 5 美元的场景比使用 10 美元的场景多,要尽可能的保留 5 美元的钞票。如果这两种组合方式都不通知,则无法正确找零,返回 False。
+由于顾客只能给我们 $5$、$10$、$20$ 三种面额的钞票,且一开始我们手头没有任何钞票,所以我们手中所能拥有的钞票面额只能是 $5$、$10$、$20$。因此可以采取下面的策略:
-所以,我们使用 five 和 ten 来维护手中 5 美元、10 美团的钞票数量, 然后遍历一遍根据上述条件分别判断即可。
+1. 如果顾客支付 $5$ 美元,直接收下。
+2. 如果顾客支付 $10$ 美元,如果我们手头有 $5$ 美元面额的钞票,则找给顾客,否则无法正确找零,返回 `False`。
+3. 如果顾客支付 $20$ 美元,如果我们手头有 $1$ 张 $10$ 美元和 $1$ 张 $5$ 美元的钞票,或者有 $3$ 张 $5$ 美元的钞票,则可以找给顾客。如果两种组合方式同时存在,倾向于第 $1$ 种方式找零,因为使用 $5$ 美元的场景比使用 $10$ 美元的场景多,要尽可能的保留 $5$ 美元的钞票。如果这两种组合方式都不通知,则无法正确找零,返回 `False`。
-## 代码
+所以,我们可以使用两个变量 `five` 和 `ten` 来维护手中 $5$ 美元、$10$ 美团的钞票数量, 然后遍历一遍根据上述条件分别判断即可。
+
+### 思路 1:代码
```Python
class Solution:
@@ -49,3 +83,8 @@ class Solution:
return True
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(n)$,其中 $n$ 是数组 `bill` 的长度。
+- **空间复杂度**:$O(1)$。
+
diff --git "a/Solutions/0881. \346\225\221\347\224\237\350\211\207.md" "b/Solutions/0881. \346\225\221\347\224\237\350\211\207.md"
index 739020c2..f6420feb 100644
--- "a/Solutions/0881. \346\225\221\347\224\237\350\211\207.md"
+++ "b/Solutions/0881. \346\225\221\347\224\237\350\211\207.md"
@@ -5,26 +5,51 @@
## 题目大意
-给定一个整数数组 `people` 代表每个人的体重,其中第 `i` 个人的体重为 `people[i]`。再给定一个整数 `limit`,代表每艘船可以承载的最大重量。每艘船最多可同时载两人,但条件是这些人的重量之和最多为 `limit`。
+**描述**:给定一个整数数组 `people` 代表每个人的体重,其中第 `i` 个人的体重为 `people[i]`。再给定一个整数 `limit`,代表每艘船可以承载的最大重量。每艘船最多可同时载两人,但条件是这些人的重量之和最多为 `limit`。
-要求:返回载到每一个人所需的最小船数(保证每个人都能被船载)。
+**要求**:返回载到每一个人所需的最小船数(保证每个人都能被船载)。
+
+**说明**:
+
+- $1 \le people.length \le 5 \times 10^4$。
+- $1 \le people[i] \le limit \le 3 \times 10^4$。
+
+**示例**:
+
+- 示例 1:
+
+```Python
+输入:people = [1,2], limit = 3
+输出:1
+解释:1 艘船载 (1, 2)
+```
+
+- 示例 2:
+
+```Python
+输入:people = [3,2,2,1], limit = 3
+输出:3
+解释:3 艘船分别载 (1, 2), (2) 和 (3)
+```
## 解题思路
+### 思路 1:贪心算法 + 双指针
+
暴力枚举的时间复杂度为 $O(n^2)$。使用双指针可以减少循环内的时间复杂度。
我们可以利用贪心算法的思想,让最重的和最轻的人一起走。这样一只船就可以尽可能的带上两个人。
具体做法如下:
-- 先对数组进行升序排序,使用 `ans` 记录所需最小船数。
-- 使用两个指针 `left`、`right`。`left` 指向数组开始位置,`right` 指向数组结束位置。
-- 判断 `people[left]` 和 `people[right]` 加一起是否超重。
- - 如果 `people[left] + people[right] > limit`,则让重的人上船,船数量 + 1,令 `right` 左移,继续判断。
- - 如果 `people[left] + people[right] <= limit`,则两个人都上船,船数量 + 1,并令 `left` 右移,`right` 左移,继续判断。
-- 如果 `lefft == right`,则让最后一个人上船,船数量 + 1。并返回答案。
+1. 先对数组进行升序排序,使用 `ans` 记录所需最小船数。
+2. 使用两个指针 `left`、`right`。`left` 指向数组开始位置,`right` 指向数组结束位置。
+3. 判断 `people[left]` 和 `people[right]` 加一起是否超重。
+ 1. 如果 `people[left] + people[right] > limit`,则让重的人上船,船数量 + 1,令 `right` 左移,继续判断。
+ 2. 如果 `people[left] + people[right] <= limit`,则两个人都上船,船数量 + 1,并令 `left` 右移,`right` 左移,继续判断。
+4. 如果 `lefft == right`,则让最后一个人上船,船数量 + 1。并返回答案。
-## 代码
+### 思路 1:代码
```Python
class Solution:
@@ -45,3 +70,8 @@ class Solution:
return ans
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(n \times \log n)$,其中 $n$ 是数组 `people` 的长度。
+- **空间复杂度**:$O(\log n)$。
+
diff --git "a/Solutions/1710. \345\215\241\350\275\246\344\270\212\347\232\204\346\234\200\345\244\247\345\215\225\345\205\203\346\225\260.md" "b/Solutions/1710. \345\215\241\350\275\246\344\270\212\347\232\204\346\234\200\345\244\247\345\215\225\345\205\203\346\225\260.md"
index b391d761..d78d7978 100644
--- "a/Solutions/1710. \345\215\241\350\275\246\344\270\212\347\232\204\346\234\200\345\244\247\345\215\225\345\205\203\346\225\260.md"
+++ "b/Solutions/1710. \345\215\241\350\275\246\344\270\212\347\232\204\346\234\200\345\244\247\345\215\225\345\205\203\346\225\260.md"
@@ -5,7 +5,7 @@
## 题目大意
-**描述**:现在需要将一些箱子装在一辆卡车 上。给定一个二维数组 `boxTypes`,其中 `boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi]`。
+**描述**:现在需要将一些箱子装在一辆卡车上。给定一个二维数组 `boxTypes`,其中 `boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi]`。
`numberOfBoxesi` 是类型 `i` 的箱子的数量。``numberOfUnitsPerBoxi` 是类型 `i` 的每个箱子可以装载的单元数量。
@@ -35,6 +35,13 @@
单元总数 = (1 * 3) + (2 * 2) + (1 * 1) = 8
```
+- 示例 2:
+
+```Python
+输入:boxTypes = [[5,10],[2,5],[4,7],[3,9]], truckSize = 10
+输出:91
+```
+
## 解题思路
### 思路 1:贪心算法
@@ -73,3 +80,8 @@ class Solution:
break
return res
```
+
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(n \times \log n)$,其中 $n$ 是数组 `boxTypes` 的长度。
+- **空间复杂度**:$O(\log n)$。
diff --git "a/Solutions/1925. \347\273\237\350\256\241\345\271\263\346\226\271\345\222\214\344\270\211\345\205\203\347\273\204\347\232\204\346\225\260\347\233\256.md" "b/Solutions/1925. \347\273\237\350\256\241\345\271\263\346\226\271\345\222\214\344\270\211\345\205\203\347\273\204\347\232\204\346\225\260\347\233\256.md"
index 0b4ff32e..e64d1598 100644
--- "a/Solutions/1925. \347\273\237\350\256\241\345\271\263\346\226\271\345\222\214\344\270\211\345\205\203\347\273\204\347\232\204\346\225\260\347\233\256.md"
+++ "b/Solutions/1925. \347\273\237\350\256\241\345\271\263\346\226\271\345\222\214\344\270\211\345\205\203\347\273\204\347\232\204\346\225\260\347\233\256.md"
@@ -5,13 +5,14 @@
## 题目大意
-**描述**:给你一个整数 `n`。
+**描述**:给你一个整数 $n$。
**要求**:请你返回满足 $1 \le a, b, c \le n$ 的平方和三元组的数目。
**说明**:
-- **平方和三元组**:指的是满足 $a^2 + b^2 = c^2$ 的整数三元组 `(a, b, c)` 。
+- **平方和三元组**:指的是满足 $a^2 + b^2 = c^2$ 的整数三元组 $(a, b, c)$。
+- $1 \le n \le 250$。
**示例**:
@@ -20,20 +21,28 @@
```Python
输入 n = 5
输出 2
-解释 平方和三元组为 (3,4,5) 和 (4,3,5) 。
+解释 平方和三元组为 (3,4,5) 和 (4,3,5)。
+```
+
+- 示例 2:
+
+```Python
+输入:n = 10
+输出:4
+解释:平方和三元组为 (3,4,5),(4,3,5),(6,8,10) 和 (8,6,10)。
```
## 解题思路
-### 思路 1:枚举算法。
+### 思路 1:枚举算法
-我们可以在 `[1, n]` 区间中枚举整数三元组 `(a, b, c)` 中的 `a` 和 `b`。然后判断 $a^2 + b^2$ 是否小于等于 `n`,并且是完全平方数。
+我们可以在 $[1, n]$ 区间中枚举整数三元组 $(a, b, c)$ 中的 $a$ 和 $b$。然后判断 $a^2 + b^2$ 是否小于等于 $n$,并且是完全平方数。
-在遍历枚举的同时,我们维护一个用于统计平方和三元组数目的变量 `cnt`。如果符合要求,则将计数 `cnt` 加 `1`。最终,我们返回该数目作为答案。
+在遍历枚举的同时,我们维护一个用于统计平方和三元组数目的变量 `cnt`。如果符合要求,则将计数 `cnt` 加 $1$。最终,我们返回该数目作为答案。
利用枚举算法统计平方和三元组数目的时间复杂度为 $O(n^2)$。
-- 注意:在计算中,为了防止浮点数造成的误差,并且两个相邻的完全平方正数之间的距离一定大于 `1`,所以我们可以用 $\sqrt{a^2 + b^2 + 1}$ 来代替 $\sqrt{a^2 + b^2}$。
+- 注意:在计算中,为了防止浮点数造成的误差,并且两个相邻的完全平方正数之间的距离一定大于 $1$,所以我们可以用 $\sqrt{a^2 + b^2 + 1}$ 来代替 $\sqrt{a^2 + b^2}$。
### 思路 1:代码
@@ -48,3 +57,8 @@ class Solution:
cnt += 1
return cnt
```
+
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(n^2)$。
+- **空间复杂度**:$O(1)$。
diff --git "a/Solutions/2249. \347\273\237\350\256\241\345\234\206\345\206\205\346\240\274\347\202\271\346\225\260\347\233\256.md" "b/Solutions/2249. \347\273\237\350\256\241\345\234\206\345\206\205\346\240\274\347\202\271\346\225\260\347\233\256.md"
new file mode 100644
index 00000000..932d76dd
--- /dev/null
+++ "b/Solutions/2249. \347\273\237\350\256\241\345\234\206\345\206\205\346\240\274\347\202\271\346\225\260\347\233\256.md"
@@ -0,0 +1,89 @@
+# [2249. 统计圆内格点数目](https://leetcode.cn/problems/count-lattice-points-inside-a-circle/)
+
+- 标签:几何、数组、哈希表、数学、枚举
+- 难度:中等
+
+## 题目大意
+
+**描述**:给定一个二维整数数组 `circles`。其中 `circles[i] = [xi, yi, ri]` 表示网格上圆心为 `(xi, yi)` 且半径为 `ri` 的第 $i$ 个圆。
+
+**要求**:返回出现在至少一个圆内的格点数目。
+
+**说明**:
+
+- **格点**:指的是整数坐标对应的点。
+- 圆周上的点也被视为出现在圆内的点。
+- $1 \le circles.length \le 200$。
+- $circles[i].length == 3$。
+- $1 \le xi, yi \le 100$。
+- $1 \le ri \le min(xi, yi)$。
+
+**示例**:
+
+- 示例 1:
+
+
+
+```Python
+输入:circles = [[2,2,1]]
+输出:5
+解释:
+给定的圆如上图所示。
+出现在圆内的格点为 (1, 2)、(2, 1)、(2, 2)、(2, 3) 和 (3, 2),在图中用绿色标识。
+像 (1, 1) 和 (1, 3) 这样用红色标识的点,并未出现在圆内。
+因此,出现在至少一个圆内的格点数目是 5。
+```
+
+- 示例 2:
+
+```Python
+输入:circles = [[2,2,2],[3,4,1]]
+输出:16
+解释:
+给定的圆如上图所示。
+共有 16 个格点出现在至少一个圆内。
+其中部分点的坐标是 (0, 2)、(2, 0)、(2, 4)、(3, 2) 和 (4, 4)。
+```
+
+## 解题思路
+
+### 思路 1:枚举算法
+
+题目要求中 $1 \le xi, yi \le 100$,$1 \le ri \le min(xi, yi)$。则圆中点的范围为 $1 \le x, y \le 200$。
+
+我们可以枚举所有坐标和所有圆,检测该坐标是否在圆中。
+
+为了优化枚举范围,我们可以先遍历一遍所有圆,计算最小、最大的 $x$、$y$ 范围,再枚举所有坐标和所有圆,并进行检测。
+
+### 思路 1:代码
+
+```Python
+class Solution:
+ def countLatticePoints(self, circles: List[List[int]]) -> int:
+ min_x, min_y = 200, 200
+ max_x, max_y = 0, 0
+ for circle in circles:
+ if circle[0] + circle[2] > max_x:
+ max_x = circle[0] + circle[2]
+ if circle[0] - circle[2] < min_x:
+ min_x = circle[0] - circle[2]
+ if circle[1] + circle[2] > max_y:
+ max_y = circle[1] + circle[2]
+ if circle[1] - circle[2] < min_y:
+ min_y = circle[1] - circle[2]
+
+ ans = 0
+ for x in range(min_x, max_x + 1):
+ for y in range(min_y, max_y + 1):
+ for xi, yi, ri in circles:
+ if (xi - x) * (xi - x) + (yi - y) * (yi - y) <= ri * ri:
+ ans += 1
+ break
+
+ return ans
+```
+
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(x \times y)$,其中 $x$、$y$ 分别为横纵坐标的个数。
+- **空间复杂度**:$O(1)$。
diff --git "a/Solutions/2427. \345\205\254\345\233\240\345\255\220\347\232\204\346\225\260\347\233\256.md" "b/Solutions/2427. \345\205\254\345\233\240\345\255\220\347\232\204\346\225\260\347\233\256.md"
new file mode 100644
index 00000000..9b083854
--- /dev/null
+++ "b/Solutions/2427. \345\205\254\345\233\240\345\255\220\347\232\204\346\225\260\347\233\256.md"
@@ -0,0 +1,58 @@
+# [2427. 公因子的数目](https://leetcode.cn/problems/number-of-common-factors/)
+
+- 标签:数学、枚举、数论
+- 难度:简单
+
+## 题目大意
+
+**描述**:给定两个正整数 $a$ 和 $b$。
+
+**要求**:返回 $a$ 和 $b$ 的公因子数目。
+
+**说明**:
+
+- **公因子**:如果 $x$ 可以同时整除 $a$ 和 $b$,则认为 $x$ 是 $a$ 和 $b$ 的一个公因子。
+- $1 \le a, b \le 1000$。
+
+**示例**:
+
+- 示例 1:
+
+```Python
+输入:a = 12, b = 6
+输出:4
+解释:12 和 6 的公因子是 1、2、3、6。
+```
+
+- 示例 2:
+
+```Python
+输入:a = 25, b = 30
+输出:2
+解释:25 和 30 的公因子是 1、5。
+```
+
+## 解题思路
+
+### 思路 1:枚举算法
+
+最直接的思路就是枚举所有 $[1, min(a, b)]$ 之间的数,并检查是否能同时整除 $a$ 和 $b$。
+
+当然,因为 $a$ 与 $b$ 的公因子肯定不会超过 $a$ 与 $b$ 的最大公因数,则我们可以直接枚举 $[1, gcd(a, b)]$ 之间的数即可,其中 $gcd(a, b)$ 是 $a$ 与 $b$ 的最大公约数。
+
+### 思路 1:代码
+
+```Python
+class Solution:
+ def commonFactors(self, a: int, b: int) -> int:
+ ans = 0
+ for i in range(1, math.gcd(a, b) + 1):
+ if a % i == 0 and b % i == 0:
+ ans += 1
+ return ans
+```
+
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$O(\sqrt{min(a, b)})$。
+- **空间复杂度**:$O(1)$。
diff --git "a/Solutions/\345\211\221\346\214\207 Offer 57 - II. \345\222\214\344\270\272s\347\232\204\350\277\236\347\273\255\346\255\243\346\225\260\345\272\217\345\210\227.md" "b/Solutions/\345\211\221\346\214\207 Offer 57 - II. \345\222\214\344\270\272s\347\232\204\350\277\236\347\273\255\346\255\243\346\225\260\345\272\217\345\210\227.md"
index 32b3b9a4..1eae5a76 100644
--- "a/Solutions/\345\211\221\346\214\207 Offer 57 - II. \345\222\214\344\270\272s\347\232\204\350\277\236\347\273\255\346\255\243\346\225\260\345\272\217\345\210\227.md"
+++ "b/Solutions/\345\211\221\346\214\207 Offer 57 - II. \345\222\214\344\270\272s\347\232\204\350\277\236\347\273\255\346\255\243\346\225\260\345\272\217\345\210\227.md"
@@ -22,6 +22,13 @@
输出:[[2,3,4],[4,5]]
```
+- 示例 2:
+
+```Python
+输入:target = 15
+输出:[[1,2,3,4,5],[4,5,6],[7,8]]
+```
+
## 解题思路
### 思路 1:枚举算法
@@ -32,13 +39,13 @@
具体步骤如下:
-- 使用列表变量 `res` 作为答案数组。
-- 使用一重循环 `i`,用于枚举序列开始位置,枚举范围为 `[1, target // 2]`。
-- 使用变量 `cur_sum` 维护当前区间的区间和,`cur_sum` 初始为 `0`。
-- 使用第 `2` 重循环 `j`,用于枚举序列的结束位置,枚举范围为 `[i, target - 1]`,并累积计算当前区间的区间和,即 `cur_sum += j`。
- - 如果当前区间的区间和大于 `target`,则跳出循环。
- - 如果当前区间的区间和等于 `target`,则将区间上的元素保存为列表,并添加到答案数组中,然后跳出第 `2` 重循环。
-- 遍历完返回答案数组。
+1. 使用列表变量 `res` 作为答案数组。
+2. 使用一重循环 `i`,用于枚举序列开始位置,枚举范围为 `[1, target // 2]`。
+3. 使用变量 `cur_sum` 维护当前区间的区间和,`cur_sum` 初始为 `0`。
+4. 使用第 `2` 重循环 `j`,用于枚举序列的结束位置,枚举范围为 `[i, target - 1]`,并累积计算当前区间的区间和,即 `cur_sum += j`。
+ 1. 如果当前区间的区间和大于 `target`,则跳出循环。
+ 2. 如果当前区间的区间和等于 `target`,则将区间上的元素保存为列表,并添加到答案数组中,然后跳出第 `2` 重循环。
+5. 遍历完返回答案数组。
### 思路 1:代码
@@ -61,6 +68,11 @@ class Solution:
return res
```
+### 思路 1:复杂度分析
+
+- **时间复杂度**:$target \times \sqrt{target}$。
+- **空间复杂度**:$O(1)$。
+
### 思路 2:滑动窗口
具体做法如下:
@@ -94,3 +106,7 @@ class Solution:
return res
```
+### 思路 2:复杂度分析
+
+- **时间复杂度**:$O(target)$。
+- **空间复杂度**:$O(1)$。