如果你可以在任何阻碍者抓住你 之前 到达目的地(阻碍者可以采取任意行动方式),则被视为逃脱成功。如果你和阻碍者 同时 到达了一个位置(包括目的地) 都不算 是逃脱成功。
-只有在你有可能成功逃脱时,输出 true ;否则,输出 false 。
如果不管阻碍者怎么移动都可以成功逃脱时,输出 true ;否则,输出 false 。
示例 1:
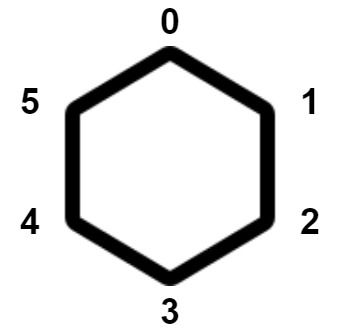
diff --git a/solution/1300-1399/1312.Minimum Insertion Steps to Make a String Palindrome/README_EN.md b/solution/1300-1399/1312.Minimum Insertion Steps to Make a String Palindrome/README_EN.md index d12812c16fe47..611f88cfd83d2 100644 --- a/solution/1300-1399/1312.Minimum Insertion Steps to Make a String Palindrome/README_EN.md +++ b/solution/1300-1399/1312.Minimum Insertion Steps to Make a String Palindrome/README_EN.md @@ -59,7 +59,7 @@ class Solution: if s[i] == s[j]: return dfs(i + 1, j - 1) return 1 + min(dfs(i + 1, j), dfs(i, j - 1)) - + return dfs(0, len(s) - 1) ``` diff --git a/solution/2500-2599/2550.Count Collisions of Monkeys on a Polygon/README.md b/solution/2500-2599/2550.Count Collisions of Monkeys on a Polygon/README.md index 1ac2a1a5cd6fa..52e81045616a8 100644 --- a/solution/2500-2599/2550.Count Collisions of Monkeys on a Polygon/README.md +++ b/solution/2500-2599/2550.Count Collisions of Monkeys on a Polygon/README.md @@ -8,7 +8,7 @@现在有一个正凸多边形,其上共有 n 个顶点。顶点按顺时针方向从 0 到 n - 1 依次编号。每个顶点上 正好有一只猴子 。下图中是一个 6 个顶点的凸多边形。


每个猴子同时移动到相邻的顶点。顶点 i 的相邻顶点可以是:
(i - 1 + n) % n 。如果移动后至少有两个猴子位于同一顶点,则会发生 碰撞 。
+如果移动后至少有两只猴子停留在同一个顶点上或者相交在一条边上,则会发生 碰撞 。
返回猴子至少发生 一次碰撞 的移动方法数。由于答案可能非常大,请返回对 109+7 取余后的结果。
示例 1:
-输入:n = 3 ++输入:n = 3 输出:6 解释:共计 8 种移动方式。 下面列出两种会发生碰撞的方式: @@ -38,7 +39,8 @@示例 2:
-输入:n = 4 ++输入:n = 4 输出:14 解释:可以证明,有 14 种让猴子碰撞的方法。diff --git a/solution/2600-2699/2605.Form Smallest Number From Two Digit Arrays/README.md b/solution/2600-2699/2605.Form Smallest Number From Two Digit Arrays/README.md new file mode 100644 index 0000000000000..d68811e583ec5 --- /dev/null +++ b/solution/2600-2699/2605.Form Smallest Number From Two Digit Arrays/README.md @@ -0,0 +1,339 @@ +# [2605. 从两个数字数组里生成最小数字](https://leetcode.cn/problems/form-smallest-number-from-two-digit-arrays) + +[English Version](/solution/2600-2699/2605.Form%20Smallest%20Number%20From%20Two%20Digit%20Arrays/README_EN.md) + +## 题目描述 + + + +给你两个只包含 1 到 9 之间数字的数组nums1和nums2,每个数组中的元素 互不相同 ,请你返回 最小 的数字,两个数组都 至少 包含这个数字的某个数位。 + ++ +
示例 1:
+ +输入:nums1 = [4,1,3], nums2 = [5,7] +输出:15 +解释:数字 15 的数位 1 在 nums1 中出现,数位 5 在 nums2 中出现。15 是我们能得到的最小数字。 ++ +示例 2:
+ +输入:nums1 = [3,5,2,6], nums2 = [3,1,7] +输出:3 +解释:数字 3 的数位 3 在两个数组中都出现了。 ++ ++ +
提示:
+ +
1 <= nums1.length, nums2.length <= 91 <= nums1[i], nums2[i] <= 9nums1 and nums2, return the smallest number that contains at least one digit from each array.
+
++
Example 1:
+ ++Input: nums1 = [4,1,3], nums2 = [5,7] +Output: 15 +Explanation: The number 15 contains the digit 1 from nums1 and the digit 5 from nums2. It can be proven that 15 is the smallest number we can have. ++ +
Example 2:
+ ++Input: nums1 = [3,5,2,6], nums2 = [3,1,7] +Output: 3 +Explanation: The number 3 contains the digit 3 which exists in both arrays. ++ +
+
Constraints:
+ +1 <= nums1.length, nums2.length <= 91 <= nums1[i], nums2[i] <= 9给你一个字符串 s ,一个字符 互不相同 的字符串 chars 和一个长度与 chars 相同的整数数组 vals 。
子字符串的开销 是一个子字符串中所有字符对应价值之和。空字符串的开销是 0 。
字符的价值 定义如下:
+ +chars 中,那么它的价值是它在字母表中的位置(下标从 1 开始)。
+ 'a' 的价值为 1 ,'b' 的价值为 2 ,以此类推,'z' 的价值为 26 。chars 中的位置为 i ,那么它的价值就是 vals[i] 。请你返回字符串 s 的所有子字符串中的最大开销。
+ +
示例 1:
+ +输入:s = "adaa", chars = "d", vals = [-1000] +输出:2 +解释:字符 "a" 和 "d" 的价值分别为 1 和 -1000 。 +最大开销子字符串是 "aa" ,它的开销为 1 + 1 = 2 。 +2 是最大开销。 ++ +
示例 2:
+ +输入:s = "abc", chars = "abc", vals = [-1,-1,-1] +输出:0 +解释:字符 "a" ,"b" 和 "c" 的价值分别为 -1 ,-1 和 -1 。 +最大开销子字符串是 "" ,它的开销为 0 。 +0 是最大开销。 ++ +
+ +
提示:
+ +1 <= s.length <= 105s 只包含小写英文字母。1 <= chars.length <= 26chars 只包含小写英文字母,且 互不相同 。vals.length == chars.length-1000 <= vals[i] <= 1000You are given a string s, a string chars of distinct characters and an integer array vals of the same length as chars.
The cost of the substring is the sum of the values of each character in the substring. The cost of an empty string is considered 0.
The value of the character is defined in the following way:
+ +chars, then its value is its corresponding position (1-indexed) in the alphabet.
+ 'a' is 1, the value of 'b' is 2, and so on. The value of 'z' is 26.i is the index where the character occurs in the string chars, then its value is vals[i].Return the maximum cost among all substrings of the string s.
+
Example 1:
+ ++Input: s = "adaa", chars = "d", vals = [-1000] +Output: 2 +Explanation: The value of the characters "a" and "d" is 1 and -1000 respectively. +The substring with the maximum cost is "aa" and its cost is 1 + 1 = 2. +It can be proven that 2 is the maximum cost. ++ +
Example 2:
+ ++Input: s = "abc", chars = "abc", vals = [-1,-1,-1] +Output: 0 +Explanation: The value of the characters "a", "b" and "c" is -1, -1, and -1 respectively. +The substring with the maximum cost is the empty substring "" and its cost is 0. +It can be proven that 0 is the maximum cost. ++ +
+
Constraints:
+ +1 <= s.length <= 105s consist of lowercase English letters.1 <= chars.length <= 26chars consist of distinct lowercase English letters.vals.length == chars.length-1000 <= vals[i] <= 1000给你一个下标从 0 开始的整数数组 arr 和一个整数 k 。数组 arr 是一个循环数组。换句话说,数组中的最后一个元素的下一个元素是数组中的第一个元素,数组中第一个元素的前一个元素是数组中的最后一个元素。
你可以执行下述运算任意次:
+ +arr 中任意一个元素,并使其值加上 1 或减去 1 。执行运算使每个长度为 k 的 子数组 的元素总和都相等,返回所需要的最少运算次数。
子数组 是数组的一个连续部分。
+ ++ +
示例 1:
+ +输入:arr = [1,4,1,3], k = 2 +输出:1 +解释:在下标为 1 的元素那里执行一次运算,使其等于 3 。 +执行运算后,数组变为 [1,3,1,3] 。 +- 0 处起始的子数组为 [1, 3] ,元素总和为 4 +- 1 处起始的子数组为 [3, 1] ,元素总和为 4 +- 2 处起始的子数组为 [1, 3] ,元素总和为 4 +- 3 处起始的子数组为 [3, 1] ,元素总和为 4 ++ +
示例 2:
+ +输入:arr = [2,5,5,7], k = 3 +输出:5 +解释:在下标为 0 的元素那里执行三次运算,使其等于 5 。在下标为 3 的元素那里执行两次运算,使其等于 5 。 +执行运算后,数组变为 [5,5,5,5] 。 +- 0 处起始的子数组为 [5, 5, 5] ,元素总和为 15 +- 1 处起始的子数组为 [5, 5, 5] ,元素总和为 15 +- 2 处起始的子数组为 [5, 5, 5] ,元素总和为 15 +- 3 处起始的子数组为 [5, 5, 5] ,元素总和为 15 ++ +
+ +
提示:
+ +1 <= k <= arr.length <= 1051 <= arr[i] <= 109You are given a 0-indexed integer array arr and an integer k. The array arr is circular. In other words, the first element of the array is the next element of the last element, and the last element of the array is the previous element of the first element.
You can do the following operation any number of times:
+ +arr and increase or decrease it by 1.Return the minimum number of operations such that the sum of each subarray of length k is equal.
A subarray is a contiguous part of the array.
+ ++
Example 1:
+ ++Input: arr = [1,4,1,3], k = 2 +Output: 1 +Explanation: we can do one operation on index 1 to make its value equal to 3. +The array after the operation is [1,3,1,3] +- Subarray starts at index 0 is [1, 3], and its sum is 4 +- Subarray starts at index 1 is [3, 1], and its sum is 4 +- Subarray starts at index 2 is [1, 3], and its sum is 4 +- Subarray starts at index 3 is [3, 1], and its sum is 4 ++ +
Example 2:
+ ++Input: arr = [2,5,5,7], k = 3 +Output: 5 +Explanation: we can do three operations on index 0 to make its value equal to 5 and two operations on index 3 to make its value equal to 5. +The array after the operations is [5,5,5,5] +- Subarray starts at index 0 is [5, 5, 5], and its sum is 15 +- Subarray starts at index 1 is [5, 5, 5], and its sum is 15 +- Subarray starts at index 2 is [5, 5, 5], and its sum is 15 +- Subarray starts at index 3 is [5, 5, 5], and its sum is 15 ++ +
+
Constraints:
+ +1 <= k <= arr.length <= 1051 <= arr[i] <= 109现有一个含 n 个顶点的 双向 图,每个顶点按从 0 到 n - 1 标记。图中的边由二维整数数组 edges 表示,其中 edges[i] = [ui, vi] 表示顶点 ui 和 vi 之间存在一条边。每对顶点最多通过一条边连接,并且不存在与自身相连的顶点。
返回图中 最短 环的长度。如果不存在环,则返回 -1 。
环 是指以同一节点开始和结束,并且路径中的每条边仅使用一次。
+ ++ +
示例 1:
+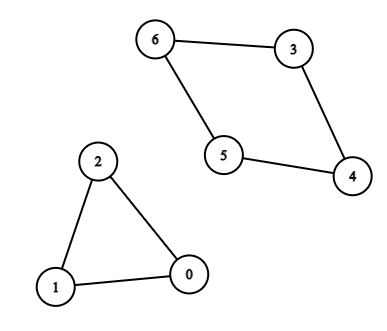 +
+输入:n = 7, edges = [[0,1],[1,2],[2,0],[3,4],[4,5],[5,6],[6,3]] +输出:3 +解释:长度最小的循环是:0 -> 1 -> 2 -> 0 ++ +
示例 2:
+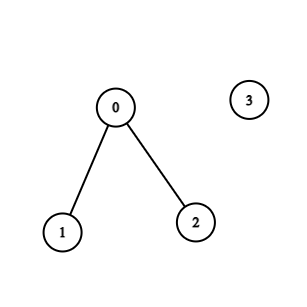 +
+输入:n = 4, edges = [[0,1],[0,2]] +输出:-1 +解释:图中不存在循环 ++ +
+ +
提示:
+ +2 <= n <= 10001 <= edges.length <= 1000edges[i].length == 20 <= ui, vi < nui != viThere is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1. The edges in the graph are represented by a given 2D integer array edges, where edges[i] = [ui, vi] denotes an edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
Return the length of the shortest cycle in the graph. If no cycle exists, return -1.
A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.
+ ++
Example 1:
+ +
++Input: n = 7, edges = [[0,1],[1,2],[2,0],[3,4],[4,5],[5,6],[6,3]] +Output: 3 +Explanation: The cycle with the smallest length is : 0 -> 1 -> 2 -> 0 ++ +
Example 2:
+ +
++Input: n = 4, edges = [[0,1],[0,2]] +Output: -1 +Explanation: There are no cycles in this graph. ++ +
+
Constraints:
+ +2 <= n <= 10001 <= edges.length <= 1000edges[i].length == 20 <= ui, vi < nui != vi给你一个仅由 0 和 1 组成的二进制字符串 s 。
如果子字符串中 所有的 0 都在 1 之前 且其中 0 的数量等于 1 的数量,则认为 s 的这个子字符串是平衡子字符串。请注意,空子字符串也视作平衡子字符串。
返回 s 中最长的平衡子字符串长度。
子字符串是字符串中的一个连续字符序列。
+ ++ +
示例 1:
+ ++输入:s = "01000111" +输出:6 +解释:最长的平衡子字符串是 "000111" ,长度为 6 。 ++ +
示例 2:
+ +
+输入:s = "00111"
+输出:4
+解释:最长的平衡子字符串是 "0011" ,长度为 4 。
+
+
+示例 3:
+ ++输入:s = "111" +输出:0 +解释:除了空子字符串之外不存在其他平衡子字符串,所以答案为 0 。 ++ +
+ +
提示:
+ +1 <= s.length <= 50'0' <= s[i] <= '1'You are given a binary string s consisting only of zeroes and ones.
A substring of s is considered balanced if all zeroes are before ones and the number of zeroes is equal to the number of ones inside the substring. Notice that the empty substring is considered a balanced substring.
Return the length of the longest balanced substring of s.
A substring is a contiguous sequence of characters within a string.
+ ++
Example 1:
+ ++Input: s = "01000111" +Output: 6 +Explanation: The longest balanced substring is "000111", which has length 6. ++ +
Example 2:
+ ++Input: s = "00111" +Output: 4 +Explanation: The longest balanced substring is "0011", which has length 4. ++ +
Example 3:
+ ++Input: s = "111" +Output: 0 +Explanation: There is no balanced substring except the empty substring, so the answer is 0. ++ +
+
Constraints:
+ +1 <= s.length <= 50'0' <= s[i] <= '1'给你一个整数数组 nums 。请你创建一个满足以下条件的二维数组:
nums 中的元素。返回结果数组。如果存在多种答案,则返回其中任何一种。
+ +请注意,二维数组的每一行上可以存在不同数量的元素。
+ ++ +
示例 1:
+ +输入:nums = [1,3,4,1,2,3,1] +输出:[[1,3,4,2],[1,3],[1]] +解释:根据题目要求可以创建包含以下几行元素的二维数组: +- 1,3,4,2 +- 1,3 +- 1 +nums 中的所有元素都有用到,并且每一行都由不同的整数组成,所以这是一个符合题目要求的答案。 +可以证明无法创建少于三行且符合题目要求的二维数组。+ +
示例 2:
+ +输入:nums = [1,2,3,4] +输出:[[4,3,2,1]] +解释:nums 中的所有元素都不同,所以我们可以将其全部保存在二维数组中的第一行。 ++ +
+ +
提示:
+ +1 <= nums.length <= 2001 <= nums[i] <= nums.lengthYou are given an integer array nums. You need to create a 2D array from nums satisfying the following conditions:
nums.Return the resulting array. If there are multiple answers, return any of them.
+ +Note that the 2D array can have a different number of elements on each row.
+ ++
Example 1:
+ ++Input: nums = [1,3,4,1,2,3,1] +Output: [[1,3,4,2],[1,3],[1]] +Explanation: We can create a 2D array that contains the following rows: +- 1,3,4,2 +- 1,3 +- 1 +All elements of nums were used, and each row of the 2D array contains distinct integers, so it is a valid answer. +It can be shown that we cannot have less than 3 rows in a valid array.+ +
Example 2:
+ ++Input: nums = [1,2,3,4] +Output: [[4,3,2,1]] +Explanation: All elements of the array are distinct, so we can keep all of them in the first row of the 2D array. ++ +
+
Constraints:
+ +1 <= nums.length <= 2001 <= nums[i] <= nums.length有两只老鼠和 n 块不同类型的奶酪,每块奶酪都只能被其中一只老鼠吃掉。
下标为 i 处的奶酪被吃掉的得分为:
reward1[i] 。reward2[i] 。给你一个正整数数组 reward1 ,一个正整数数组 reward2 ,和一个非负整数 k 。
请你返回第一只老鼠恰好吃掉 k 块奶酪的情况下,最大 得分为多少。
+ +
示例 1:
+ ++输入:reward1 = [1,1,3,4], reward2 = [4,4,1,1], k = 2 +输出:15 +解释:这个例子中,第一只老鼠吃掉第 2 和 3 块奶酪(下标从 0 开始),第二只老鼠吃掉第 0 和 1 块奶酪。 +总得分为 4 + 4 + 3 + 4 = 15 。 +15 是最高得分。 ++ +
示例 2:
+ ++输入:reward1 = [1,1], reward2 = [1,1], k = 2 +输出:2 +解释:这个例子中,第一只老鼠吃掉第 0 和 1 块奶酪(下标从 0 开始),第二只老鼠不吃任何奶酪。 +总得分为 1 + 1 = 2 。 +2 是最高得分。 ++ +
+ +
提示:
+ +1 <= n == reward1.length == reward2.length <= 1051 <= reward1[i], reward2[i] <= 10000 <= k <= nThere are two mice and n different types of cheese, each type of cheese should be eaten by exactly one mouse.
A point of the cheese with index i (0-indexed) is:
reward1[i] if the first mouse eats it.reward2[i] if the second mouse eats it.You are given a positive integer array reward1, a positive integer array reward2, and a non-negative integer k.
Return the maximum points the mice can achieve if the first mouse eats exactly k types of cheese.
+
Example 1:
+ ++Input: reward1 = [1,1,3,4], reward2 = [4,4,1,1], k = 2 +Output: 15 +Explanation: In this example, the first mouse eats the 2nd (0-indexed) and the 3rd types of cheese, and the second mouse eats the 0th and the 1st types of cheese. +The total points are 4 + 4 + 3 + 4 = 15. +It can be proven that 15 is the maximum total points that the mice can achieve. ++ +
Example 2:
+ ++Input: reward1 = [1,1], reward2 = [1,1], k = 2 +Output: 2 +Explanation: In this example, the first mouse eats the 0th (0-indexed) and 1st types of cheese, and the second mouse does not eat any cheese. +The total points are 1 + 1 = 2. +It can be proven that 2 is the maximum total points that the mice can achieve. ++ +
+
Constraints:
+ +1 <= n == reward1.length == reward2.length <= 1051 <= reward1[i], reward2[i] <= 10000 <= k <= n给你一个整数 n 和一个在范围 [0, n - 1] 以内的整数 p ,它们表示一个长度为 n 且下标从 0 开始的数组 arr ,数组中除了下标为 p 处是 1 以外,其他所有数都是 0 。
同时给你一个整数数组 banned ,它包含数组中的一些位置。banned 中第 i 个位置表示 arr[banned[i]] = 0 ,题目保证 banned[i] != p 。
你可以对 arr 进行 若干次 操作。一次操作中,你选择大小为 k 的一个 子数组 ,并将它 翻转 。在任何一次翻转操作后,你都需要确保 arr 中唯一的 1 不会到达任何 banned 中的位置。换句话说,arr[banned[i]] 始终 保持 0 。
请你返回一个数组 ans ,对于 [0, n - 1] 之间的任意下标 i ,ans[i] 是将 1 放到位置 i 处的 最少 翻转操作次数,如果无法放到位置 i 处,此数为 -1 。
i ,ans[i] 相互之间独立计算。+ +
示例 1:
+ +
+输入:n = 4, p = 0, banned = [1,2], k = 4
+输出:[0,-1,-1,1]
+解释:k = 4,所以只有一种可行的翻转操作,就是将整个数组翻转。一开始 1 在位置 0 处,所以将它翻转到位置 0 处需要的操作数为 0 。
+我们不能将 1 翻转到 banned 中的位置,所以位置 1 和 2 处的答案都是 -1 。
+通过一次翻转操作,可以将 1 放到位置 3 处,所以位置 3 的答案是 1 。
+
+
+示例 2:
+ ++输入:n = 5, p = 0, banned = [2,4], k = 3 +输出:[0,-1,-1,-1,-1] +解释:这个例子中 1 一开始在位置 0 处,所以此下标的答案为 0 。 +翻转的子数组长度为 k = 3 ,1 此时在位置 0 处,所以我们可以翻转子数组 [0, 2],但翻转后的下标 2 在 banned 中,所以不能执行此操作。 +由于 1 没法离开位置 0 ,所以其他位置的答案都是 -1 。 ++ +
示例 3:
+ ++输入:n = 4, p = 2, banned = [0,1,3], k = 1 +输出:[-1,-1,0,-1] +解释:这个例子中,我们只能对长度为 1 的子数组执行翻转操作,所以 1 无法离开初始位置。 ++ +
+ +
提示:
+ +1 <= n <= 1050 <= p <= n - 10 <= banned.length <= n - 10 <= banned[i] <= n - 11 <= k <= n banned[i] != pbanned 中的值 互不相同 。You are given an integer n and an integer p in the range [0, n - 1]. Representing a 0-indexed array arr of length n where all positions are set to 0's, except position p which is set to 1.
You are also given an integer array banned containing some positions from the array. For the ith position in banned, arr[banned[i]] = 0, and banned[i] != p.
You can perform multiple operations on arr. In an operation, you can choose a subarray with size k and reverse the subarray. However, the 1 in arr should never go to any of the positions in banned. In other words, after each operation arr[banned[i]] remains 0.
Return an array ans where for each i from [0, n - 1], ans[i] is the minimum number of reverse operations needed to bring the 1 to position i in arr, or -1 if it is impossible.
ans[i] are independent for all i's.+
Example 1:
+ ++Input: n = 4, p = 0, banned = [1,2], k = 4 +Output: [0,-1,-1,1] +Explanation: In this case+ +k = 4so there is only one possible reverse operation we can perform, which is reversing the whole array. Initially, 1 is placed at position 0 so the amount of operations we need for position 0 is0. We can never place a 1 on the banned positions, so the answer for positions 1 and 2 is-1. Finally, with one reverse operation we can bring the 1 to index 3, so the answer for position 3 is1. +
Example 2:
+ ++Input: n = 5, p = 0, banned = [2,4], k = 3 +Output: [0,-1,-1,-1,-1] +Explanation: In this case the 1 is initially at position 0, so the answer for that position is+ +0. We can perform reverse operations of size 3. The 1 is currently located at position 0, so we need to reverse the subarray[0, 2]for it to leave that position, but reversing that subarray makes position 2 have a 1, which shouldn't happen. So, we can't move the 1 from position 0, making the result for all the other positions-1. +
Example 3:
+ ++Input: n = 4, p = 2, banned = [0,1,3], k = 1 +Output: [-1,-1,0,-1] +Explanation: In this case we can only perform reverse operations of size 1. So the 1 never changes its position. ++ +
+
Constraints:
+ +1 <= n <= 1050 <= p <= n - 10 <= banned.length <= n - 10 <= banned[i] <= n - 11 <= k <= n banned[i] != pbanned are unique