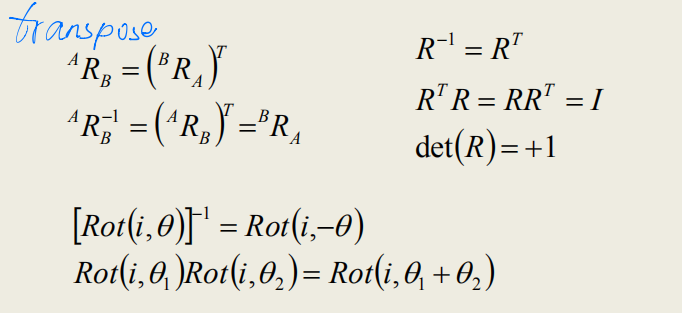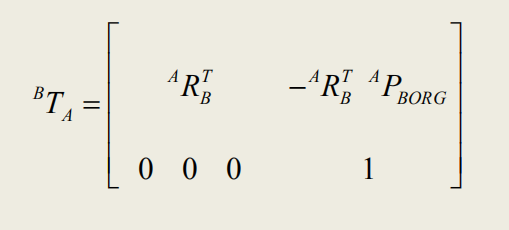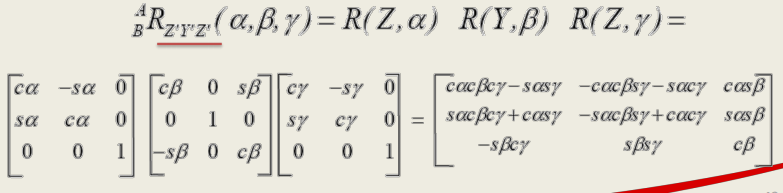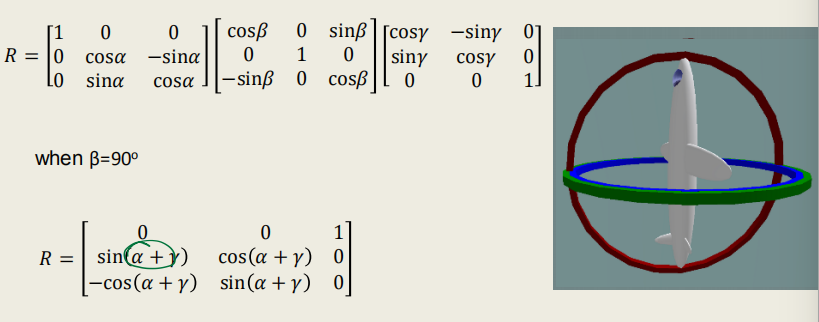| title | date | categories | tags | slug | ||||
|---|---|---|---|---|---|---|---|---|
理解机器人学的Singularity |
2019-10-03 22:19:27 +0100 |
|
|
robotics-singularity |
Before understanding the singularities in robotics, we shall review:
- What are
rotation matrices? - What are
Euler angles?p
I think these two points are the bases of the comprehension of singularities.
- 计算什么?
end-effector的位置(和速度) - 用什么算?
joint parameters的指定值
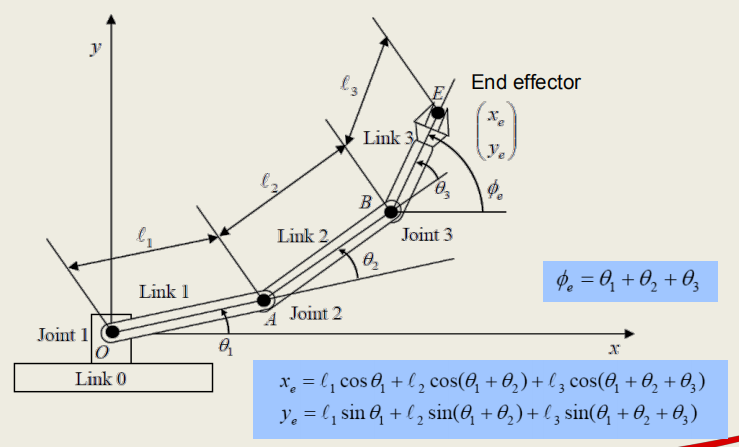
Forward kinematics refers to the use of the kinematic equations of a robot to compute the position of the end-effector from specified values for the joint parameters. [bib1]
- 使用joint处的相对夹角$\theta$而不是与x轴的夹角,是为了便于joint处的motor的建模
说明end-effector的位置是通过对每一个joint处的方向和长度确定的,关节和关节之间存在位置平移和方向旋转的关系。
Right-handed coordinates system is more widely-used. It should be indicated in specific tutorials of a robot.
- x axis: thumb
- y axis: index finger
- z axis: middle finger
About: Rotation & Translation of frames.
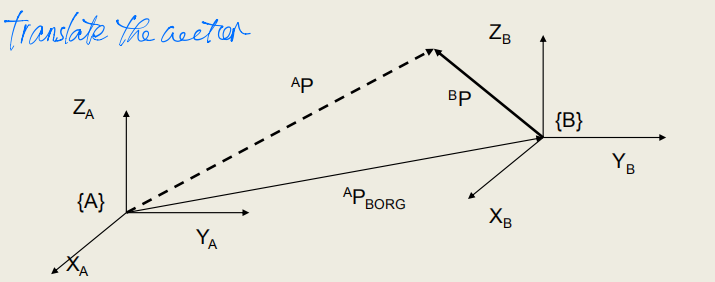
参考轴系间的平移。
只translation: $$ \begin{equation} ^{A}P = ^{B}{P} + ^A{P_{BORG}} \end{equation}\label{eq2} $$
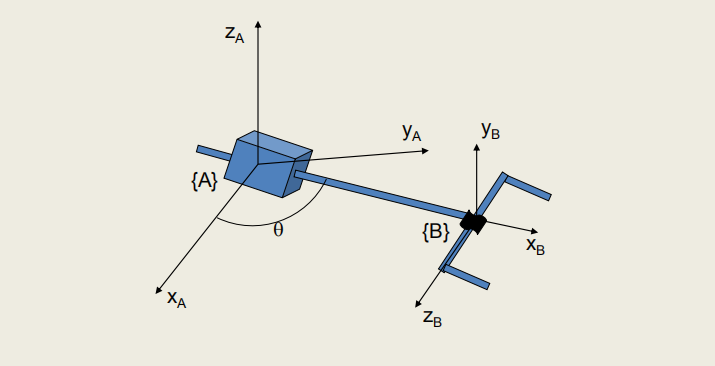
参考轴系之间的旋转关系。
Moving from axes in {A} to axes in {B}.从A系到B系的位置关系。
i.e. a description of {B} w.r.t. {A}相对于A系B系的空间位置。
已知在{a}系中点p的坐标,那么将{b}系绕原点(三维坐标系中即绕z轴)正向旋转角度$\theta$,那么{b}系中的坐标将可以通过三角(trigonometry)几何关系得到。
{b}系p点坐标作为需要求的,是从{a}系信息求的。那么反过来,用{b}系的点坐标得到相应在{a}中的坐标,见下面的公式。那么这时候{b}到{a}的旋转应理解为反向旋转$\theta$,这样公式才正确。 $$ \begin{equation} ^ap_x = ^bp_xcos\theta - ^bp_ysin\theta \\ ^ap_y = ^bp_ycos\theta + ^bp_xsin\theta \end{equation}\label{eq4} $$
可以写成矩阵形式 $$ \begin{equation} \left[ \begin{matrix} ^ap_x\\^ap_y \end{matrix} \right] =\left[ \begin{matrix} cos\theta & -sin\theta\\ sin\theta & cos\theta \end{matrix} \right] \left[ \begin{matrix} ^bp_x\\^bp_y \end{matrix} \right] \end{equation}\label{eq5} $$
需要一个好理解的公式,来表示两个frames的旋转关系: $$ \begin{equation}^{A}P = ^{A}R_B{^B{P}} \end{equation}\label{eq6} $$
或者表示为$P_A = R_{AB}{P_B}$ 或
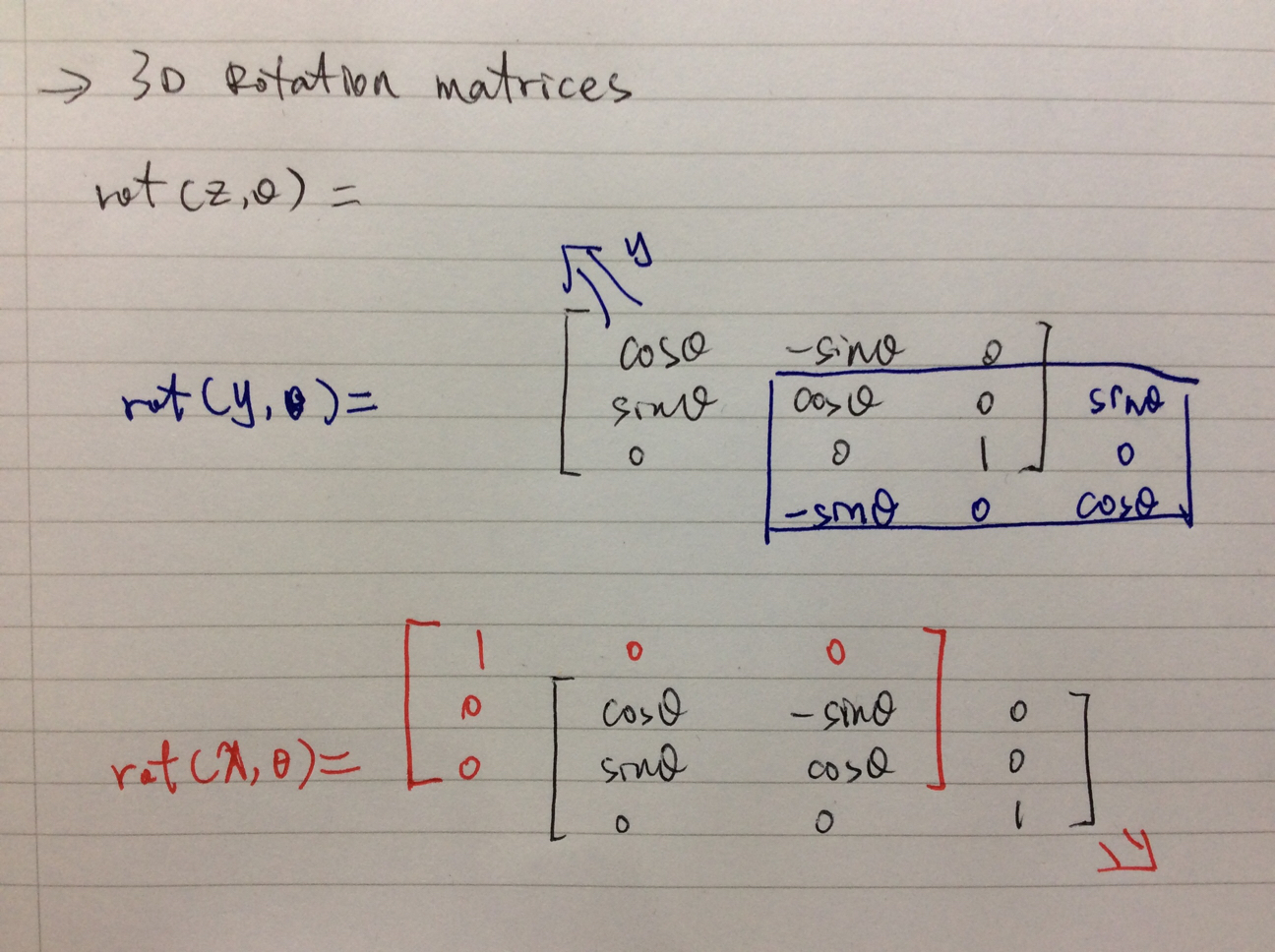
在上面的情况中,z轴都没有做过变换,所以位置向量的z分量应该还不变:$^ap_z=^bp_z$。那么三维的旋转矩阵表示为:
上面的说的只是绕z轴旋转的情况,那么对于任意一个轴旋转,都有对应的旋转矩阵,这里旋转指除旋转轴之外的轴往负方向旋转。
Q: 这也太难记了吧?我可咋整啊?即使通过原来联立的方程组也很难算啊......
A: 我有个特殊的记忆方法:
黑色框表示绕z轴的旋转矩阵,要得到蓝色的绕y旋转矩阵,就往左上角推,右下角四个元素为新旋转矩阵的左上角四个元素,被挤出去的[1,1]位置元素就只能躲右下角,其他四个元素被分别挤到同一个路线上的四个位置,知道贪吃蛇吗?就这感觉。
得到了旋转矩阵,那我们如果知道了一个参考系中的位置向量(在后面理解为目标位置的,相对于“那一个位置”的参考系的位置向量),要求出经过旋转的参考系的同一个位置向量(在后面理解为旋转到目标位置之前,“那一个位置”的参考系的位置向量),就需要知道旋转角是多少(这样才得到旋转矩阵)。
证明过程如下:
对于下方的两个公式,证明只需要想,从{B}系反向旋转$\theta$ 到{A}系,就相当于反过来旋转$-\theta$ 角;同理,两次旋转矩阵相当于一次旋转了两个旋转角之和。 $$ \begin{equation} \left[ Rot(i,\theta) \right]^{-1}= Rot(i,-\theta)\\ Rot(i,\theta_1)Rot(i,\theta_2)= Rot(i,\theta_1+\theta_2) \end{equation}\label{eq9} $$
🗒️ 还有种好记的方法:旋转矩阵的每一行就是{A}的坐标轴在{B}中的表示。
对于特殊角度$90^\circ$ ,可以根据正交向量来表示,见后文。
根据旋转矩阵的性质,可以看出来他们都是正交矩阵(orthogonal matrix)[bib2]。
注:要区别于对称矩阵(symmetric matrix):$A=A^T$ 和反对称矩阵(skew-symmetric matrix):$A^T=-A$
从上面的回顾中我们知道:
- 位置变换通过向量来表示
- 角度/方向变换矩阵来表示
那么两个系之间同时存在translation和rotation怎么表示呢? $$ \begin{equation} ^AP=^AR_B{^BP}+^AP_{BORG} \end{equation}\label{eq11} $$
注意了,说明是先旋转,再平移!见Order matters?
- [0 0 0]是perspective transformation
- 1是scaling factor
**这个矩阵是怎么得出来的?**参考推导齐次变换矩阵
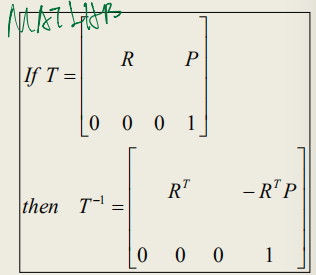
看到没?逆变换矩阵还是用之前的正变换旋转矩阵和平移向量来表示的,是正变换矩阵的逆矩阵。
证明很简单,只要按块求逆就行。
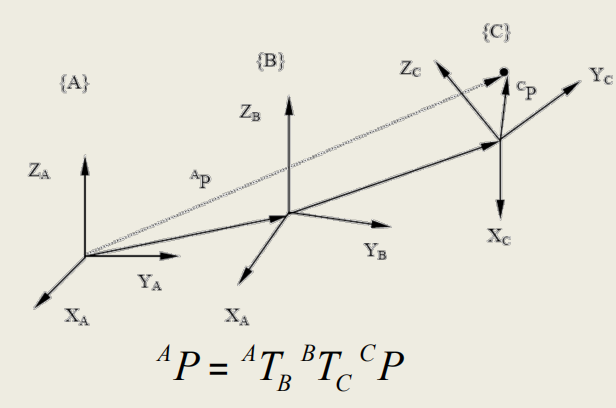
知道在一个系里的位置向量,以及系之间的变换关系,就可以得到”最远的“系中的位置向量。
前面讲变换的公式时,有说先旋转再平移,那么为什么必须这样规定呢?
从数学角度理解, $$ \begin{equation} \begin{aligned} rot\rightarrow trans: \quad ^AP&=^AR_B{^BP}+^AP_{BORG}\\ trans\rightarrow rot: \quad ^AP&=^AR_B({^BP}+^AP_{BORG}) \end{aligned} \end{equation}\label{eq12} $$ 不希望的结果是: 绕自己几何中心以外位置的原点的旋转 (地球公转式) 和缩放。
可以看出先平移之后,表面上看旋转会让平移向量也发生旋转,实际上坐标系原点已经发生了变化,$^AR_B$ 本来定义就是绕着{A}{B}系的公共原点(或者处于同一空间位置的公共轴)进行旋转得到的旋转矩阵,平移导致旋转轴不再重合,原本的位置向量$^BP$ 相对于新坐标系相当于被改变了模长,这时的旋转矩阵即使作用了,也只是对${^BP}+^AP_{BORG}$ 作用,经过变换之后得到的位置向量和另一种顺序变换得到的不一样。
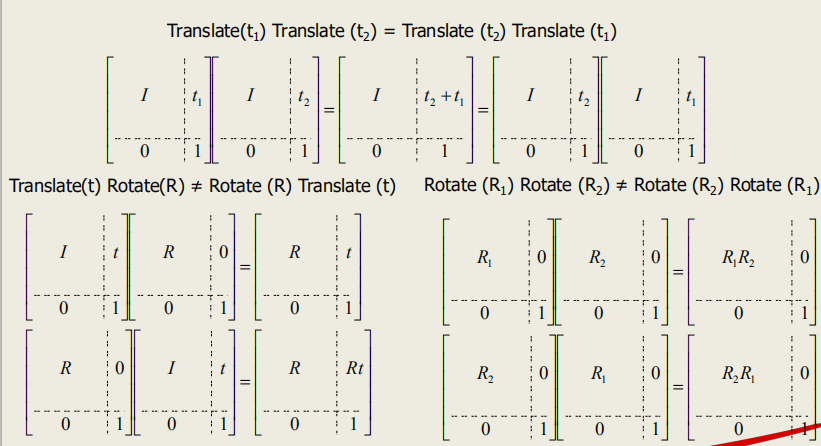
下图的矩阵运算可证明,旋转和平移不具有交换性。
Need a proof.
- 用三个角度表示方向
- 常常按照是绕X, Y, Z轴的旋转顺序来规定
- 旋转顺序称为
Euler Angle Sequence - Minimal representation of orientation
理解齐次坐标和齐次矩阵:
上面两图说明,变换为ZYZ时,$\beta=0^\circ ,or,180^\circ$时,求解公式的分母会变成0,因此对于最后一个旋转角度$\alpha$来说,由于第一次旋转的角度$\gamma$已经定了,$\alpha$将无意义。
换一种方式理解,分析一个实例:Gimbal lock。
它采用XYZ convention,根据compound transformations,写出关系式: $$ ^A_BR_{XYZ}=R(x,\alpha)R(y,\beta)R(z,\gamma) $$ 将它们展开,进行矩阵的乘法得到结果: $$ \begin{equation} \begin{aligned} ^A_BR_{XYZ}= \left[ \begin{matrix} cos\beta cos\gamma & -sin\gamma cos\beta & sin\beta \\ sin\alpha sin\beta cos\gamma + cos\alpha sin\gamma & -sin\beta sin\alpha sin\gamma + cos\alpha cos\gamma & -sin\alpha cos\beta \\ -sin\beta cos\alpha cos\gamma + sin\alpha sin\gamma & sin\beta cos\alpha sin\gamma + sin\alpha cos\gamma & cos\alpha cos\beta \end{matrix} \right] \end{aligned} \end{equation}\label{eq14} $$ 当$\beta = 90^\circ$时,代入$sin\beta, cos\beta$,变为: $$ \begin{equation} \begin{aligned} ^A_BR_{XYZ}= \left[ \begin{matrix} 0 & 0 & 1 \\ sin(\alpha + \gamma) & cos(\alpha +\gamma) & 0 \\ -cos(\alpha +\gamma) & sin(\alpha + \gamma) & 0 \end{matrix} \right] \end{aligned} \end{equation}\label{eq15} $$ "This is exactly the same effective Gimbal lock causing two circular arms to rotate on the same plane"
此时说明,第二个旋转角为$90^\circ$时,第三次旋转和第一次旋转是一样的效果。$\gamma$角已经完成变换,$\beta$导致最后一次旋转变换,即$\alpha$角的转动,和$\gamma$角的转动共旋转轴,少了一个自由度。在上式中体现为两角变成整体的变量,无论$\alpha$不变,还是$\gamma$改变和$\gamma$不变,$\alpha$改变,结果会往同一中趋势改变。这种情况就是奇点(singularity),一般发生在joints line up的时候,两个自由度产生重合。
下面引用一个经典的视频来说明这种自由度减少情况:
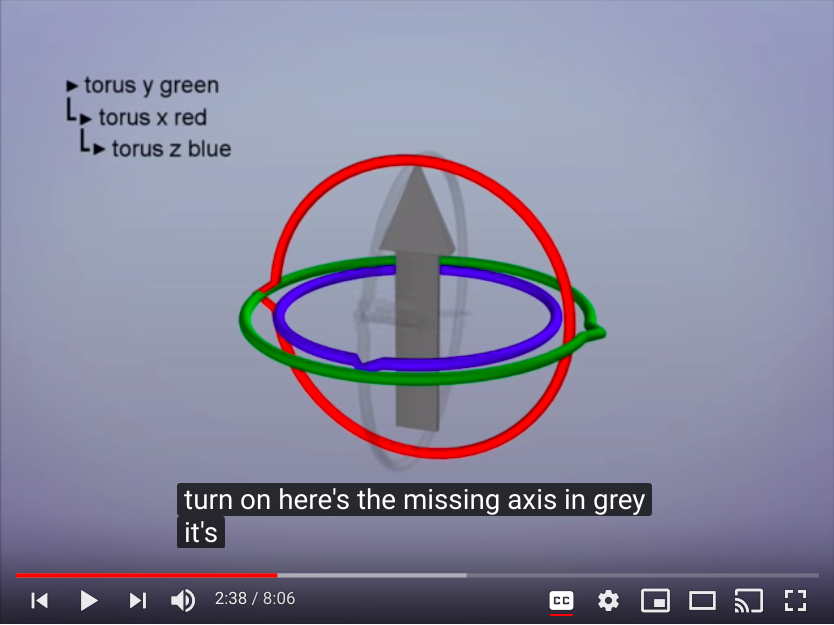
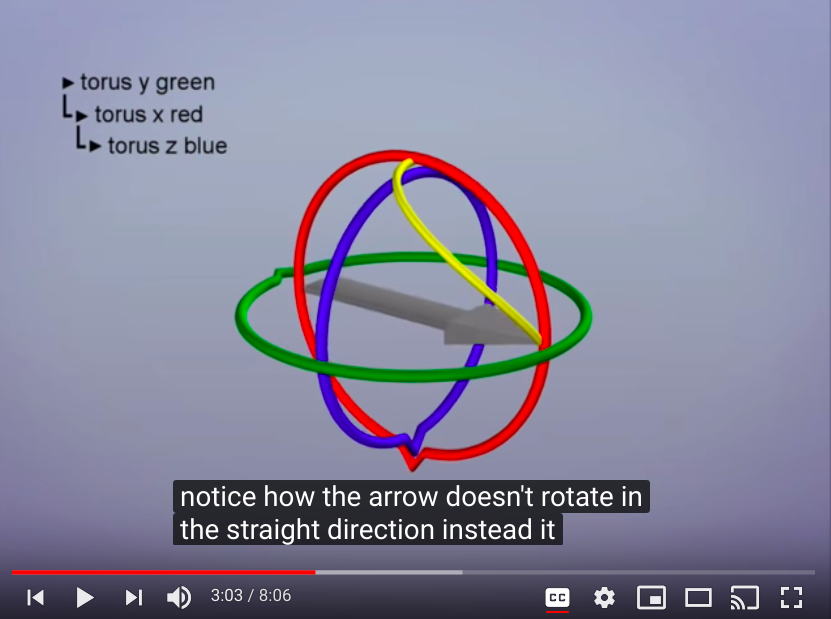
<style>.embed-container { position: relative; padding-bottom: 56.25%; height: 0; overflow: hidden; max-width: 100%; } .embed-container iframe, .embed-container object, .embed-container embed { position: absolute; top: 0; left: 0; width: 100%; height: 100%; }</style>出现下图的情况时,Gimbal lock已经发生,我们想让箭头指向其他位置而不是正上方,但是已经缺少可以让其变换到其他位置的自由度了,图中灰色的torus就是我们想要而得不到的圆环面。
z blue torus: roll
y green torus: yaw or heading or pan
x red torus: pitch or tilt
那怎么办?只能重新再来一次animation,变动多个torus来实现指向。
It's always possible to rotate our arrow into any new rotation but we have to rotate all three axes to achieve it.
lock之后再做旋转运动的结果就是,end-effector箭头不会按照直线走,而是沿着一个不确定的弧线移动,这样的在两个位置状态之间的移动具有多样性和不确定性,不好控制。
具体来讲,奇点会带来哪些危害呢?
- manipulator会失去至少一个自由度,无法实现某些运动
- 加载在某些joint variables(比如角速度,或我理解的比如PWM波驱动舵机)上的改变怎么也不会导致end-effector做出对应的位置和方向改变。要是设计得不好,机器人是不是很容易剧烈运动?即使没有到达奇点位置,运动速度也会突然加快,整体将不稳定
- 无法求逆运算[bib3]
逆运算是逆运动学。
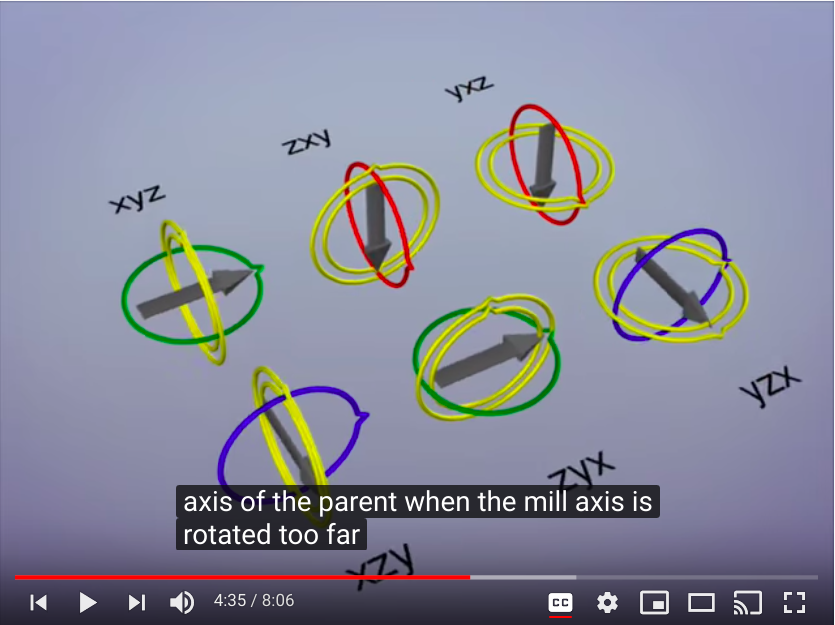
在另一种convention中,如YZX就可以实现箭头指向正上方了还可以转动再往下指,但这并不代表这种convention就不存在Gimbal lock了,只是换了个位置。实际上,任何一种变换都会存在singularity,要具体问题具体分析。
那我们知道singularity情况下,机器人会有运动的不确定性了,那应该怎么减少这种情况呢?
With any object, the key if to find a rotation order that has the least chance of hitting gimbal. So the trick here is to find the direction that the object least likely to face.
- 找到最可不常需要面对的位置,将此位置设计为singularity,我们就能避免在其他常规运动时碰到singularity啦!
- 如果确实没办法或者暂时没办法解决,那么在奇点处设计奇点触发保护也是很好的。[bib3]
最后再以一个展示六轴机器人出现三种类型singularity情况的视频收尾。它们分别是wrist singularities, elbow singularities and shoulder singularities。视频作者Mecademic有更加详细的根据六轴机器人来分析singularity的文章:What are singularities in a six-axis robot arm?,马住便于以后学了复杂一点的机器人之后再回顾。
https://en.wikipedia.org/wiki/Forward_kinematics#cite_note-1