This is an implemtation for NIPS paper: Triangle Generative Adversarial Networks
tensorflow 1.1.0, python 2.7;
For domain transfer and classification task, CelebA and MSCOCO dataset need to be in HDF5 format;
For semi-supervised learning tasks, please see here
For domain transfer and classification task: If you want to re-run the CelebA experiment, the feature can be downloaded here: CelebA tag features
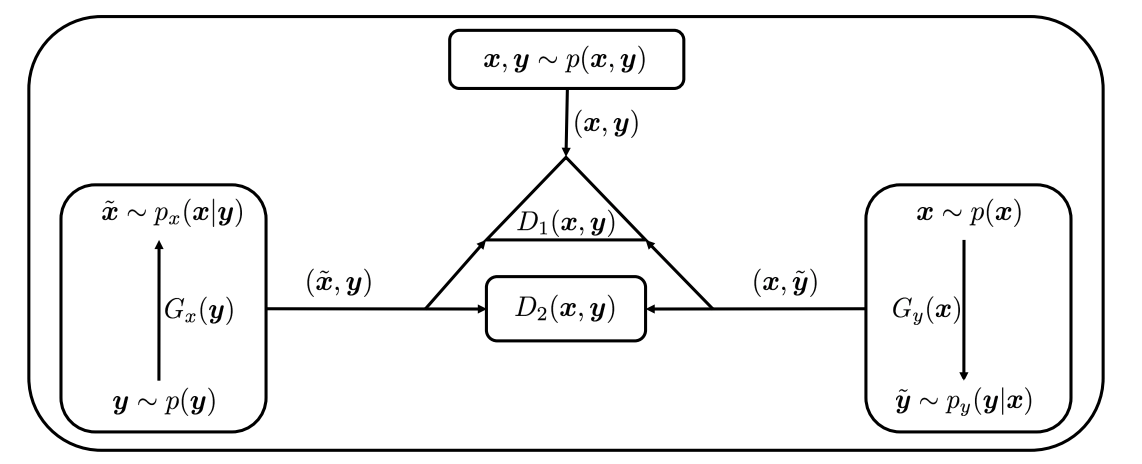
Here's is our model:
The value function for TriGAN model:
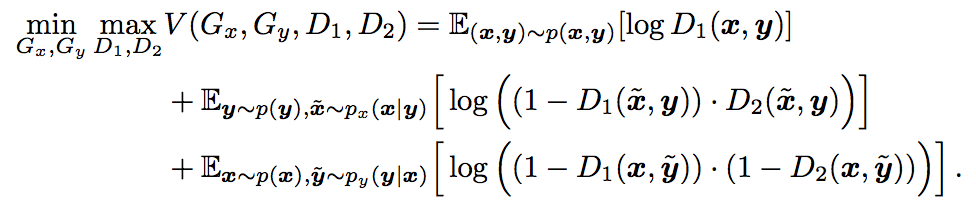 The objective of
The objective of
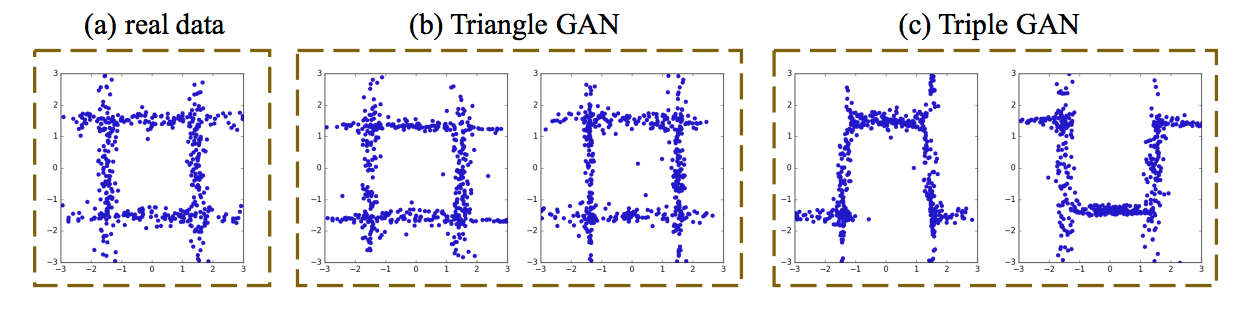
figure (a): the joint distribution
figure (b):
figure (c): Tirple GAN without regularization terms
left: the joint distribution