Normal searching algorithm using Ternary Search Trees for Searching and Auto-Completion... We have been storing large-scale data like phonebook data in the form of BSTs and Maps. However, this method is not so efficient since users may not get the desired results in an efficient manner. Compromises are to be made either in terms of time complexity or in terms of memory utilization. This calls for a better design of a system wherein people can easily retrieve info without wasting much time. This project has been designed to overcome this problem.
This system is developed keeping in view the general need required by the user while requiring searching and/or closest-record searching while using any given data. For example, a phone directory book or a database of movies. The users will have the ability to efficiently store and retrieve information with these functionalities.
Ternary Search Trees are a Data Structure similar to Binary Search Trees, the only difference being that each node includes three children. BST’s require rearrangement of entire data which accounts for extreme inefficiency when a dataset is very large. To counter this, the data structures trie’s can be used where each node has 26 children each corresponding to a possibility in the english alphabet. We would also need to include special characters and spaces which would only add to the extremely large amounts of space the trie would take up, be it only in storing the large amount of null pointers. Ternary Search Trees take care of both of these issues by not requiring any rearrangement, while not taking up too much space. The project has a wide array of implementations, ranging from using it to search usernames to movie names from a database.
In order to demonstrate the power of this project, we will be implementing the user being able to search phrases / nearest-matching phrases in a directory containing a large number of .txt files. If no such phrase is available, the closest-matching phrase along will be displayed as per user input provided to the system.
Project Objectives To demonstrate the power of using ternary search trees for searching a large amount of data, very quickly while not taking up a lot of space as is the case with Tries. We plan to do this by using them for providing autocomplete and closest suggestion to a search term present in given files.
The dataset can be as large as the phonebook of a city or a directory containing a large number of research papers. To provide a demonstration for a general case, we have implemented in-file searching for any given files. The files can be given in the form of a directory path and more than one files can be added (not necessarily in the same directory).
“IntelliSearch” has been designed to computerize the following functions that are performed by the system: Search/Autocomplete for a given term FAST- You will be able to find a given term provided a list of source files. Memory Efficient- Using ternary tree as the primary data structure ensures that we do not tradeoff heavily on memory for gains in speed of searching/autocompletion. ● Specify Multiple Files- You can specify multiple files among which you want to search your text from. CLI- You can pass all the filepaths as parameters while running the executable directly from the CLI using the -f flag.
Data Structures Used are -
● Ternary Search Trees
● Vectors
● Searching
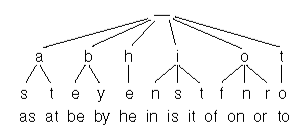
We know of Binary Search Trees where each node has at most two children/subtrees. Tries are k-ary trees. Unlike BST’s a node in a trie doesn’t store its associated key, instead its position in the tree determines that key.
A common application of Tries is seen in string-searching algorithms however they come with the drawback of taking up enormous amounts of space.
A ternary search tree is a special trie data structure where the child nodes of a standard trie are ordered as a binary search tree. It has three children, a left subtree, a right subtree and a mid or an equal subtree.
The information stored in a trie for performing fast string-searching can be stored in ternary search trees, making it more efficient by reducing the storage requirements considerably.