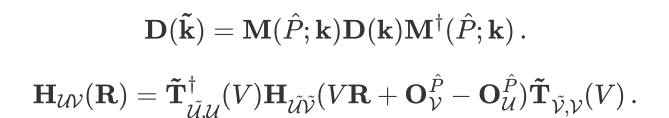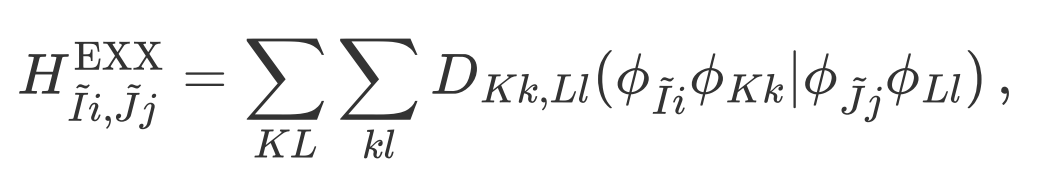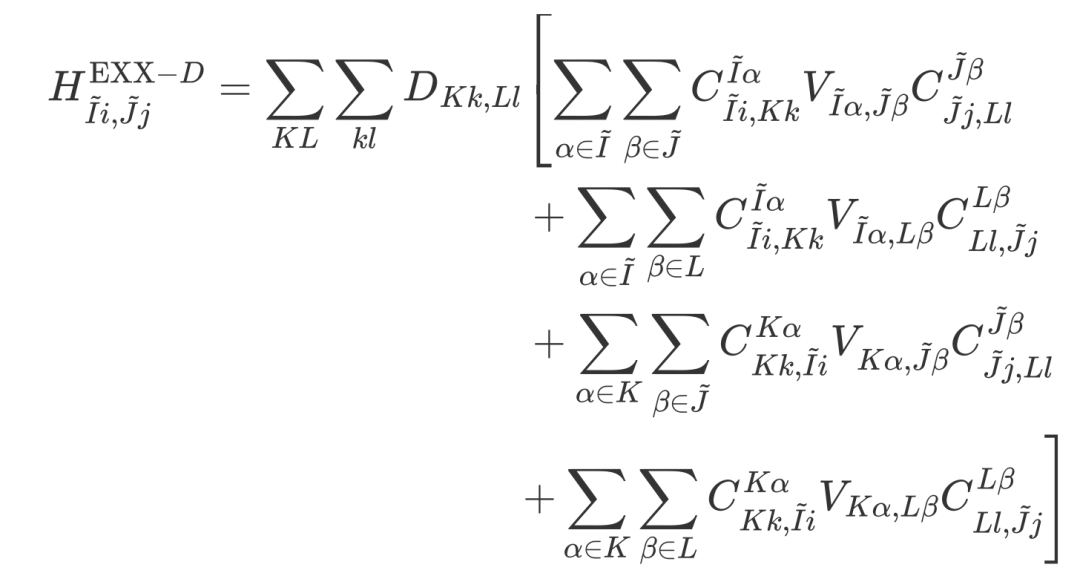From 5d676a3f4deb9b1358aa0519a393406a717588cb Mon Sep 17 00:00:00 2001
From: YB_HU <138468445+RussellHu41@users.noreply.github.com>
Date: Thu, 9 Oct 2025 17:09:59 +0800
Subject: [PATCH] Create ABACUS_30_09_2025.md
---
source/_posts/ABACUS_30_09_2025.md | 90 ++++++++++++++++++++++++++++++
1 file changed, 90 insertions(+)
create mode 100644 source/_posts/ABACUS_30_09_2025.md
diff --git a/source/_posts/ABACUS_30_09_2025.md b/source/_posts/ABACUS_30_09_2025.md
new file mode 100644
index 0000000..6682f8c
--- /dev/null
+++ b/source/_posts/ABACUS_30_09_2025.md
@@ -0,0 +1,90 @@
+---
+title: "What Can ABACUS Do Too? | Accelerating Hybrid Functional Calculations with Numerical Atomic Orbital Basis Sets Using Space-Group Symmetry"
+date: 2025-9-30
+categories:
+- ABACUS
+---
+
+Hybrid functionals (HDFs) overcome the shortcomings of local/semi-local functionals—such as the underestimation of band gaps—by incorporating exact exchange (EXX), but this comes at the cost of high computational expense. ABACUS combined with LibRI enables linear-scaling calculations of hybrid functionals, and on this basis, applying space-group symmetry can further reduce the computational load.
+
+Prior to version 3.8.0, ABACUS already supported symmetry acceleration for local/semi-local functionals: it reduces the number of Kohn-Sham (KS) equations to be solved by reducing k-points to the irreducible Brillouin zone (IBZ). However, due to the lack of implementation for space-group transformations of the density matrix, symmetry acceleration was not supported for cases involving non-local Hamiltonians (e.g., hybrid functionals). On the other hand, symmetry reduction can also be applied to real-space two-electron integrals (ERIs) for the EXX term. Nevertheless, currently available software (such as CRYSTAL and Turbomole) only implements this for algorithms that directly compute four-center integrals, without further accelerating symmetry application based on the resolution of the identity (RI) method—a common approach to speed up ERI calculations.
+
+
+
+Recently, researchers from the Institute of Physics, Chinese Academy of Sciences, and Peking University used symmetry to accelerate two key steps in hybrid functional calculations with ABACUS+LibRI: they not only reduced the time required for diagonalization to solve the Kohn-Sham equations by means of k-point reduction, but also reduced the real-space region using symmetry. This further accelerated the calculation of the real-space EXX Hamiltonian by several times, building on the linear scaling achieved by the local resolution of the identity (LRI) method [1]. This feature is supported in ABACUS v3.8.0, LibRI v0.2.0, and later versions.
+
+The related work, titled “Applying Space-Group Symmetry to Speed Up Hybrid-Functional Calculations within the Framework of Numerical Atomic Orbitals”, was published in the Journal of Chemical Theory and Computation: https://pubs.acs.org/doi/10.1021/acs.jctc.5c00537 [2].
+
+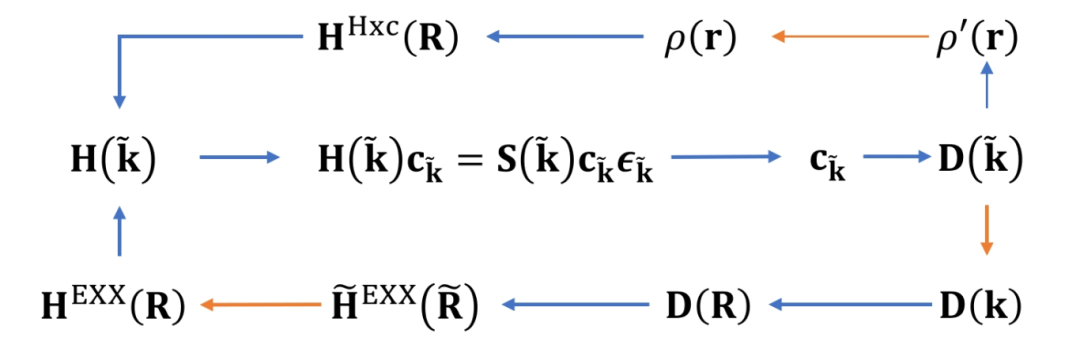 +
+*Figure 1: KSDFT workflow for hybrid functionals, where orange arrows indicate steps involving the application of symmetry.*
+
+## Research Methods
+
+For numerical atomic orbital basis sets, the transformation formulas of the k-space density matrix and real-space Hamiltonian under the space-group operation
+
+*Figure 1: KSDFT workflow for hybrid functionals, where orange arrows indicate steps involving the application of symmetry.*
+
+## Research Methods
+
+For numerical atomic orbital basis sets, the transformation formulas of the k-space density matrix and real-space Hamiltonian under the space-group operation 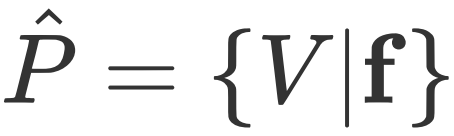 are:
+
+
are:
+
+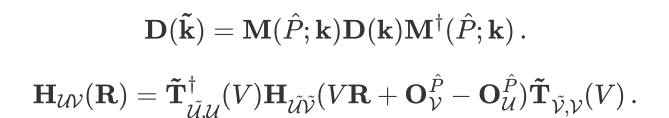 +
+Here, T and M are the rotation matrices of symmetry operations in the atomic orbital and Bloch orbital representations, respectively, which can be derived using Wigner D-matrices (see the original paper [2] for details). After applying symmetry, only the EXX Hamiltonian for atomic pairs in the irreducible region needs to be computed in real space:
+
+
+
+Here, T and M are the rotation matrices of symmetry operations in the atomic orbital and Bloch orbital representations, respectively, which can be derived using Wigner D-matrices (see the original paper [2] for details). After applying symmetry, only the EXX Hamiltonian for atomic pairs in the irreducible region needs to be computed in real space:
+
+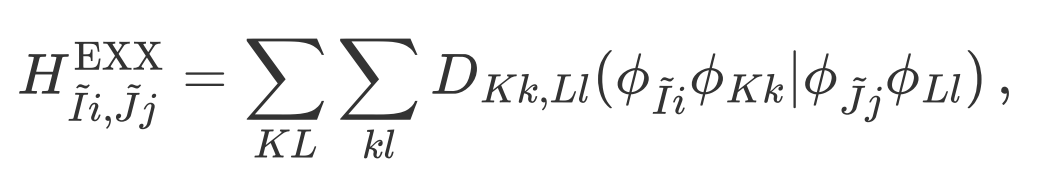 +
+The formula for converting four-center integrals to two-center integrals using the local resolution of the identity (LRI) method is:
+
+
+
+The formula for converting four-center integrals to two-center integrals using the local resolution of the identity (LRI) method is:
+
+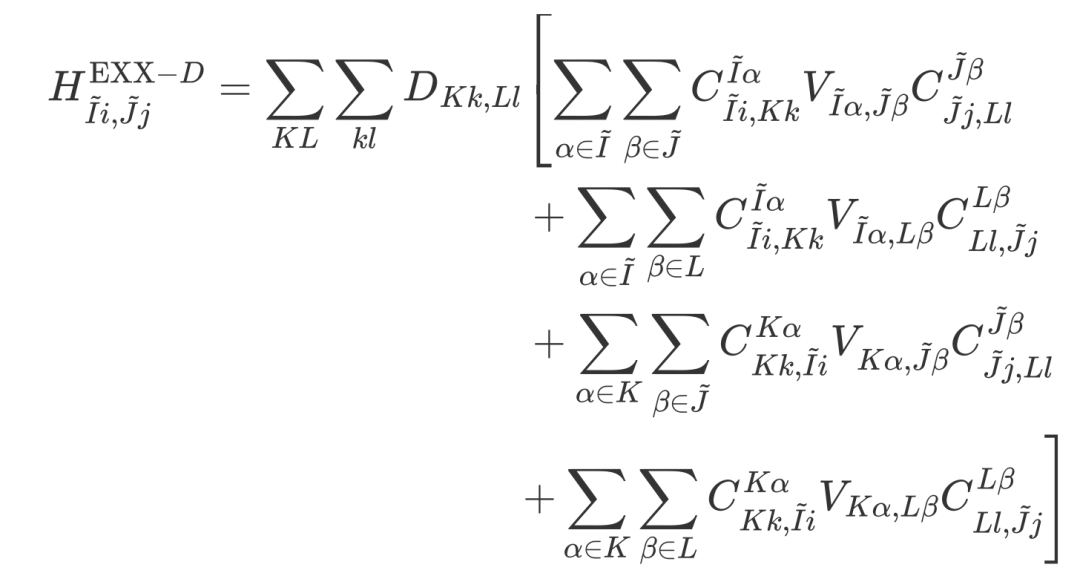 +
+Where C is the coefficient for expanding atomic orbital products using auxiliary basis sets, and V is the Coulomb matrix in the auxiliary basis representation.
+
+To reduce the redundancy of tensors across processes and save memory, LibRI computes the EXX Hamiltonian by switching from the "D perspective" to the "V perspective" [1] (as shown in Figure 2). However, when using symmetry to reduce the real-space region, this perspective switch causes the four types of terms computed simultaneously to contribute to different irreducible atomic pairs, introducing additional difficulties in screening the irreducible real-space region during code implementation.
+
+
+
+Where C is the coefficient for expanding atomic orbital products using auxiliary basis sets, and V is the Coulomb matrix in the auxiliary basis representation.
+
+To reduce the redundancy of tensors across processes and save memory, LibRI computes the EXX Hamiltonian by switching from the "D perspective" to the "V perspective" [1] (as shown in Figure 2). However, when using symmetry to reduce the real-space region, this perspective switch causes the four types of terms computed simultaneously to contribute to different irreducible atomic pairs, introducing additional difficulties in screening the irreducible real-space region during code implementation.
+
+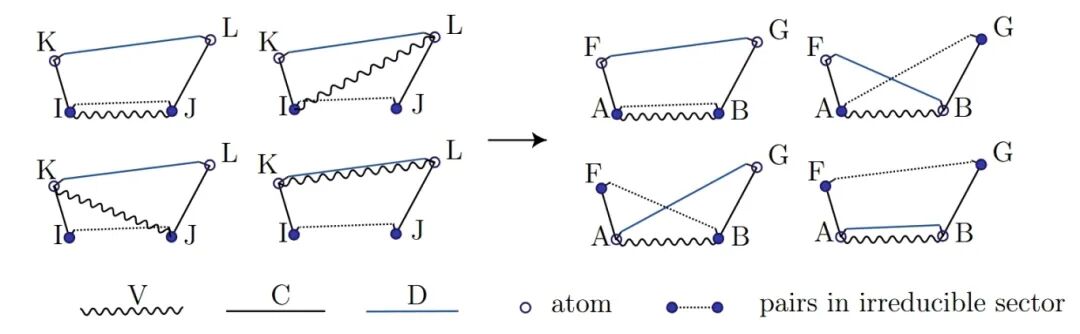 +
+*Figure 2: When switching the Hamiltonian grouping method from the D perspective to the V perspective, irreducible atomic pairs of the four term types appear at different positions.*
+
+LibRI v0.2.0 [3] has improved the underlying algorithm by reducing four nested loops to three, which reduces the computation time by an order of magnitude while resolving this difficulty: the new algorithm uniformly iterates over atoms in the irreducible region in the outermost loop and the second innermost loop when computing all types of terms.
+
+
+
+*Figure 2: When switching the Hamiltonian grouping method from the D perspective to the V perspective, irreducible atomic pairs of the four term types appear at different positions.*
+
+LibRI v0.2.0 [3] has improved the underlying algorithm by reducing four nested loops to three, which reduces the computation time by an order of magnitude while resolving this difficulty: the new algorithm uniformly iterates over atoms in the irreducible region in the outermost loop and the second innermost loop when computing all types of terms.
+
+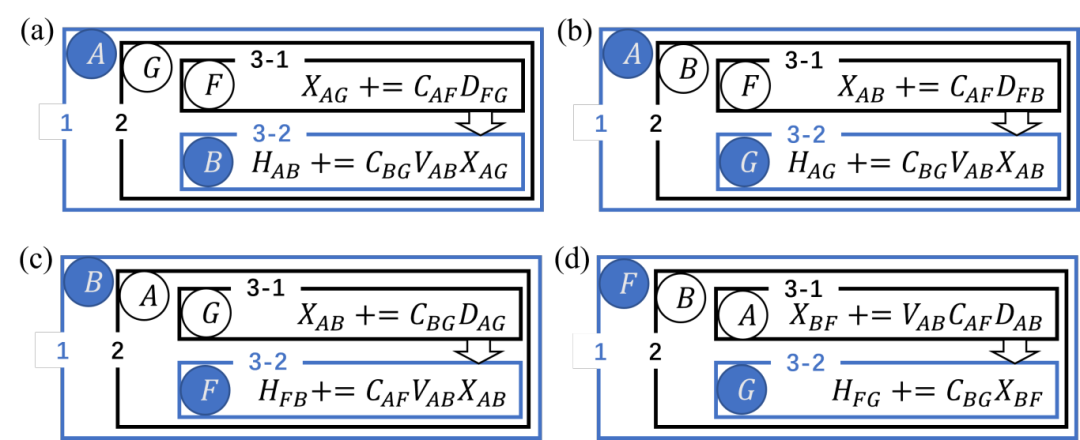 +
+*Figure 3: Schematic diagram of EXX Hamiltonian calculation with real-space irreducible region screening based on the new "loop3" algorithm in LibRI v0.2.0, where blue circles represent irreducible atomic pairs.*
+
+## Results
+
+We tested systems with various symmetries (see Table 1). The results show that:
+
+- The acceleration ratio for diagonalization is consistent with the k-point reduction factor and increases with the increase in k-point density.
+- The acceleration ratio for calculating the real-space EXX Hamiltonian varies by system:
+ - For 3D uniform k-point sampling: The acceleration ratio first increases and then decreases as k-points are densified. Due to the higher symmetry of the BvK supercell for odd k-points, the acceleration ratio for odd k-points is higher than that for even k-points (as shown in Figure 4).
+ - For 2D uniform k-point sampling: The acceleration ratio first increases with the increase in k-points and then stabilizes, with no significant fluctuation between odd and even k-points (as shown in Figure 5).
+
+Figure 6 compares the acceleration ratios of four similar structures with different symmetries. The highest symmetry (Oh) can accelerate the calculation of the real-space EXX Hamiltonian by 4–5 times.
+
+
+
+*Figure 3: Schematic diagram of EXX Hamiltonian calculation with real-space irreducible region screening based on the new "loop3" algorithm in LibRI v0.2.0, where blue circles represent irreducible atomic pairs.*
+
+## Results
+
+We tested systems with various symmetries (see Table 1). The results show that:
+
+- The acceleration ratio for diagonalization is consistent with the k-point reduction factor and increases with the increase in k-point density.
+- The acceleration ratio for calculating the real-space EXX Hamiltonian varies by system:
+ - For 3D uniform k-point sampling: The acceleration ratio first increases and then decreases as k-points are densified. Due to the higher symmetry of the BvK supercell for odd k-points, the acceleration ratio for odd k-points is higher than that for even k-points (as shown in Figure 4).
+ - For 2D uniform k-point sampling: The acceleration ratio first increases with the increase in k-points and then stabilizes, with no significant fluctuation between odd and even k-points (as shown in Figure 5).
+
+Figure 6 compares the acceleration ratios of four similar structures with different symmetries. The highest symmetry (Oh) can accelerate the calculation of the real-space EXX Hamiltonian by 4–5 times.
+
+ +
+*Table 1: Symmetry (Point Groups of Space Groups) and Number of Operations for Tested Systems*
+
+
+
+*Table 1: Symmetry (Point Groups of Space Groups) and Number of Operations for Tested Systems*
+
+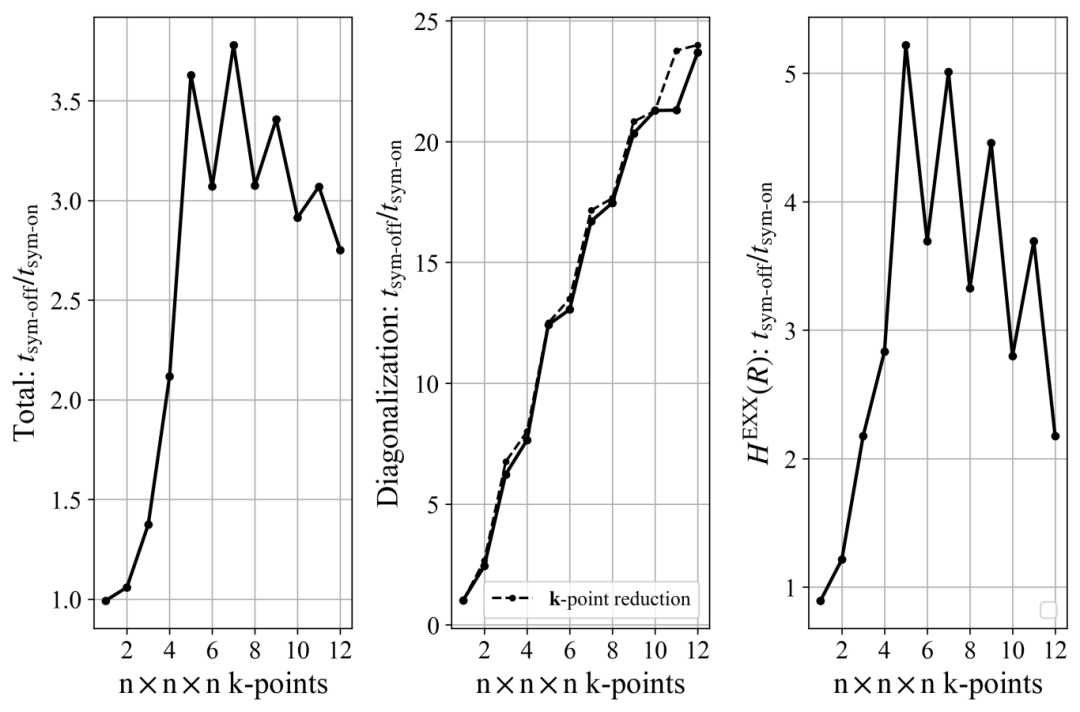 +
+*Figure 4: HSE functional calculations for crystalline silicon (Oh group), showing the variation of the overall acceleration ratio, k-space diagonalization acceleration ratio, and real-space exact exchange potential acceleration ratio with 3D uniform k-point sampling density.*
+
+
+
+*Figure 4: HSE functional calculations for crystalline silicon (Oh group), showing the variation of the overall acceleration ratio, k-space diagonalization acceleration ratio, and real-space exact exchange potential acceleration ratio with 3D uniform k-point sampling density.*
+
+ +
+*Figure 5: HSE functional calculations for MoS₂ crystals (D6h group), showing the variation of the overall acceleration ratio, k-space diagonalization acceleration ratio, and real-space exact exchange potential acceleration ratio with 2D uniform k-point sampling density.*
+
+
+
+*Figure 5: HSE functional calculations for MoS₂ crystals (D6h group), showing the variation of the overall acceleration ratio, k-space diagonalization acceleration ratio, and real-space exact exchange potential acceleration ratio with 2D uniform k-point sampling density.*
+
+ +
+*Figure 6: Acceleration ratios for HSE calculations of 4-atom Al supercells with four types of symmetry.*
+
+## Conclusion
+
+By leveraging the transformation relationships of the density matrix and Hamiltonian under symmetry operations for numerical atomic orbital basis sets, the researchers restricted k-space and real-space calculations to irreducible regions. This significantly accelerated two major time-consuming bottlenecks in the ABACUS+LibRI hybrid functional calculation workflow: "diagonalization to solve the Kohn-Sham equations" and "calculation of the exact exchange Hamiltonian".
+
+Notably, symmetry acceleration in real space was achieved for the first time on the basis of the linear-scaling acceleration of the LRI method. Furthermore, relying on LibRI's general program framework, this approach can be extended to methods beyond density functional theory, such as the GW method.
+
+
+## References
+
+[1] Peize Lin, Xinguo Ren, and Lixin He. Journal of Chemical Theory and Computation 2021, 17 (1), 222–239, DOI: 10.1021/acs.jctc.0c00960 (https://pubs.acs.org/doi/10.1021/acs.jctc.0c00960)
+
+[2] Yu Cao, Min-Ye Zhang, Peize Lin, Mohan Chen, and Xinguo Ren. Journal of Chemical Theory and Computation 2025, 21 (16), 8086–8105, DOI: 10.1021/acs.jctc.5c00537 (https://pubs.acs.org/doi/10.1021/acs.jctc.5c00537)
+
+[3] https://github.com/abacusmodeling/LibRI
+
+*Figure 6: Acceleration ratios for HSE calculations of 4-atom Al supercells with four types of symmetry.*
+
+## Conclusion
+
+By leveraging the transformation relationships of the density matrix and Hamiltonian under symmetry operations for numerical atomic orbital basis sets, the researchers restricted k-space and real-space calculations to irreducible regions. This significantly accelerated two major time-consuming bottlenecks in the ABACUS+LibRI hybrid functional calculation workflow: "diagonalization to solve the Kohn-Sham equations" and "calculation of the exact exchange Hamiltonian".
+
+Notably, symmetry acceleration in real space was achieved for the first time on the basis of the linear-scaling acceleration of the LRI method. Furthermore, relying on LibRI's general program framework, this approach can be extended to methods beyond density functional theory, such as the GW method.
+
+
+## References
+
+[1] Peize Lin, Xinguo Ren, and Lixin He. Journal of Chemical Theory and Computation 2021, 17 (1), 222–239, DOI: 10.1021/acs.jctc.0c00960 (https://pubs.acs.org/doi/10.1021/acs.jctc.0c00960)
+
+[2] Yu Cao, Min-Ye Zhang, Peize Lin, Mohan Chen, and Xinguo Ren. Journal of Chemical Theory and Computation 2025, 21 (16), 8086–8105, DOI: 10.1021/acs.jctc.5c00537 (https://pubs.acs.org/doi/10.1021/acs.jctc.5c00537)
+
+[3] https://github.com/abacusmodeling/LibRI
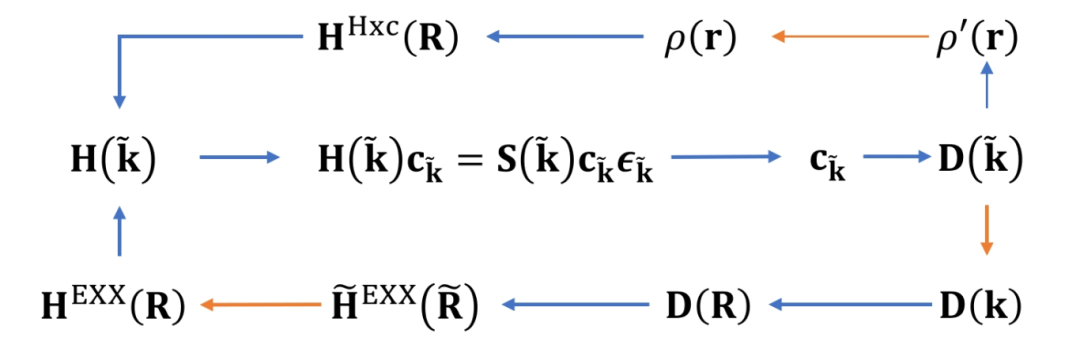
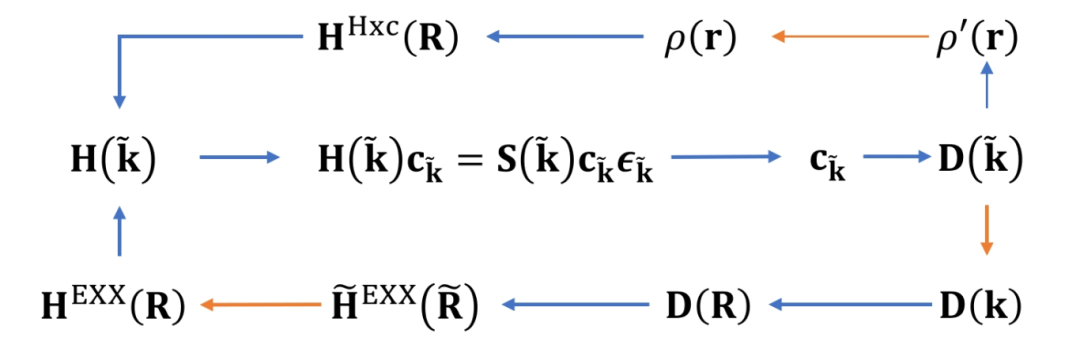
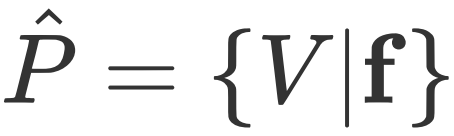 are:
+
+
are:
+
+