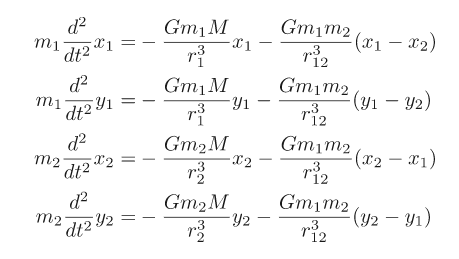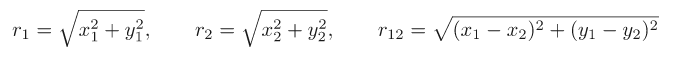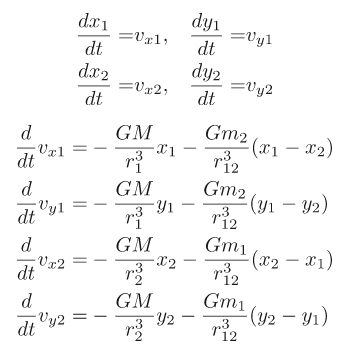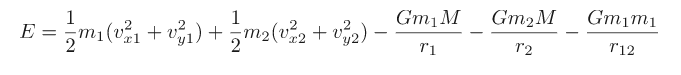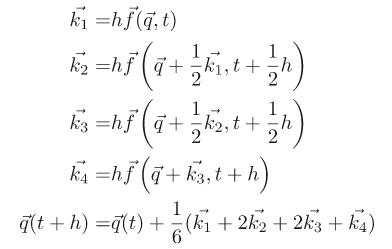Goal of the Program

In this assignment we will model the orbits of two planets (or a planet and a “moon”) about a primary (the Sun). To simplify things we restrict ourselves the motion to the $xy$ plane.

The equations of motion that arise from Newton’s second law (see below) can be written as eight coupled first-order ordinary differential equations; these equations we will integrate via 4th-order Runge Kutta.

Part I

For Part I, consider just one planet in orbit around a primary. We restrict the planet to the $xy$ plane and the primary to be fixed at the origin. The independent variable is time $t$ and the dependent variables are the positions $(x_1, y_1)$ and velocities $(v_{x1}, v_{y1})$. You can find the equations of motion below (for simplicity we set $G = 1$).

After the equations of motions are solved, the program will write into a file time $t$, positions $x_1, y_1$ and energy $E$ which ought to be conserved. You can head to jupyter to see the plots. Adjust namelist file if you want different initial conditions.

Part 2

The program should now work for two planets orbiting a primary star fixed at the origin. In this case you will have 8 dependent variables. The output now includes columns for $x_2, y_2$. There will also be graphs of this on jupyter. For different results, adjust the namelist input file.

Equations of motion

Energy

Runge Kutta fourth order:

Compiling the program

It would be quite beneficial to you if you had a Linux system because it would enable you to use the makefile included.

If this is the case then what you do is open a terminal, use the cd command to change to this directory.

Then type make.

You'll see some gfortran commands being executed. All of this has created an exectuable file called nuclear-reactor.

In order to run this executable you type ./planetary. This will make the program compile with default values which produce a circular orbit with one planet around a primary. However if you want to run a different input then you do ./planetary namelist file name Below are the available namelist files:

circular_motion.namelist - 2 planets orbitting a primary in a circle. circular_motion_part_1.namelist - 1 planet orbitting a primary in a circle. elliptical_motion_part_1.namelist - 1 planet orbitting a primary in an ellipse. moon_motion.namelist - 1 planet orbitting another planet that orbits a primary.

So, as an example, if you want the first one then you do ./planetary circular_motion.namelist

You can edit the namelist input yourself to see how the output changes, slight deviations in initial conditions can wildly change a planet's orbit!

Next you can type jupyter notebook into the terminal to see the graphs of 2 planets orbitting a primary and the moon scenario.