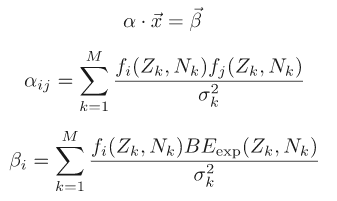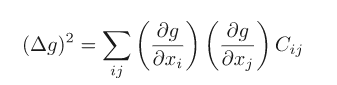Goal of the Program

Imagine you have just been awarded a NASA grant to investigate stellar nucleosynthesis. Among the most important inputs into nucleosynthesis are nuclear binding energies. The binding energy of a nucleus is the amount of energy released when a nucleus is formed from its constituent protons and neutrons, or conversely how much energy could be released if a nucleus were totally disassembled. For a nucleus with $Z$ protons and $N$ neutrons, we define

$m(Z, N)c^2 = Zm_pc^2 + Nm_nc^2 + BE(Z, N)$

where $m(Z, N)$ is the mass of the nucleus, $m_p$ is the mass of the proton, $m_n$ is the mass of the neutron and BE(Z, N) is the binding energy.

Although the binding energy has been measured experimentally for thousands of nuclei, an even larger number of short-lived isotopes exist whose binding energies are unknown and difficult if not impossible to measure, yet are very important to describe different nucleosynthesis processes. Of particular interest are the binding energies of heavy neutron-rich nuclei and the position of the neutron drip-line. Using the binding energy we can compute the neutron and proton separation energies which is the energy needed to separate a neutron or a proton from its nucleus; the drip-lines bound the regions with positive separation energies, that is, it takes energy to remove a proton or neutron. Beyond the drip-lines the separation energies are negative, meaning it requires no energy for a proton or neutron to just "drip off".

Fortunately, we can estimate the location of the drip-lines by using the semi-empirical mass formula:

$BE(Z, N) = c_{vol}A + c_{surf}A^{2/3} + c_{asym}\frac{(N-Z)^2}{A} + c_{coul}\frac{Z(Z-1)}{A^{1/3}} + c_{pair}A^{-3/4}δ(Z, N)$

where $A = Z + N$ is the mass number and $δ(Z, N)$ is 1 if $Z$ and $N$ are both even and -1 if $Z$ and $N$ are both odd and 0 if $A$ is odd.

The Atomic Mass Evaluation (AME) has compiled the most up to date value of all measured binding energies. You can find them in the EXPERIMENT_AME2016.dat file. The goal in this assignment is to determine the c parameters that best describe the experimental data and use those parameters to identify the position of the neutron dripline.

The best fit parameters from the linear model (like the semi-empirical mass formula above) can be determined by solving a set of linear equations, which in turn can be represented as a matrix equation.

where $x$ contains the parameters in the linear model, α are the matrix elements of α, β are the elements of the vector β, $M$ is the number experimental values, the functions $f_i(Z_k, N_k)$ are the ones multiplying each of the linear parameters in the semi-empirical mass formula, $BE_{exp}(Z_k, N_k) is the experimental value of each binding energy, and σ is the corresponding experimental error.

In this case α is a $5$ x $5$ matrix because the semi-empirical mass formula has 5 parameters.

Furthermore, the inverse of the matrix corresponds to the covariance matrix $C = α^{-1}$. In certain cases the covariance matrix can be used to propagate the experimental uncertainty to any quantity calculated with the model parameters $x$. If $g$ is a function that depends on the parameters $x_i$, the propagated uncertainty is given by

Now that we have our model we can find the neutron drip line. The neutron drip-line is defined as the maximum values of $N$ which correspond to bound nuclei, for a given $Z$, that is for which the 1 neutron separation energy $S_n = BE(Z, N - 1) - BE(Z, N) > 0$.

If you compare the experimental binding energies (the input from the data file) with the calculated binding energies, you will find that there are significant deviations, much larger than either the experimental errors or your calculated theoretical uncertainties. This is because of systematic variations not included in the semi-empirical formula, namely the existence of shells.

Running the program

It would be quite beneficial to you if you had a Linux system because it would enable you to use the makefile included.

If this is the case then what you do is open a terminal, use the cd command to change to this directory.

Then type make.

You'll see some gfortran commands being executed. All of this has created an exectuable file called nuclear_energies.

In order to run this executable you type ./nuclear_energies. Make sure not to put any spaces!

Now when you run this executable it'll ask you for the name of the file. The most up to date file is EXPERIMENT_AME2016.dat and is included in the src directory.

Technically you can enter any file that exists but the program expects certain data to be there that is present in the EXPERIMENT_AME2016.dat file.

Enter that file name when it asks and if you entered it correctly then you should see results written to results.dat and results_advanced.dat.

Open up the jupyter notebook file to analyze the results.