From 3717b84f55d7a1f01579507b1850a3be1cef984b Mon Sep 17 00:00:00 2001
From: alexgrover <41912104+alexgrover@users.noreply.github.com>
Date: Mon, 2 Mar 2020 18:00:27 +0100
Subject: [PATCH] Update README.md
---
techniques/dsp/README.md | 890 ++++++++++++++++++++++++++++-----------
1 file changed, 654 insertions(+), 236 deletions(-)
diff --git a/techniques/dsp/README.md b/techniques/dsp/README.md
index 4fc6406..a13da47 100644
--- a/techniques/dsp/README.md
+++ b/techniques/dsp/README.md
@@ -8,412 +8,830 @@
gtag('config', 'UA-147975914-1');
-[ ](http://pinecoders.com)
+[
](http://pinecoders.com)
+[ ](http://pinecoders.com)
-# Digital Signal Processing In Pine, by [Alex Grover](https://www.tradingview.com/u/alexgrover/#published-scripts)
+# Digital Signal Processing In Pinescript, by [Alex Grover](https://www.tradingview.com/u/alexgrover/#published-scripts)
-## Table of Contents
+
](http://pinecoders.com)
-# Digital Signal Processing In Pine, by [Alex Grover](https://www.tradingview.com/u/alexgrover/#published-scripts)
+# Digital Signal Processing In Pinescript, by [Alex Grover](https://www.tradingview.com/u/alexgrover/#published-scripts)
-## Table of Contents
+
+
+### Table of Contents
- [Introduction](#introduction)
- [Digital Signals](#digital-signals)
-- [Cross Correlation](#cross-correlation)
- [Convolution](#convolution)
-- [Impulse Function And Impulse Response](#impulse-function-and-impulse-response)
-- [Step Function And Step Response](#step-function-and-step-response)
-- [FIR Filter Design In Pine](#fir-filter-design-in-pine)
-- [Calculating Different Types Of Filters In Pine](#calculating-different-types-of-filters-in-pine)
-- [Exponential Averager](#exponential-averager)
-- [Matched Filter](#matched-filter)
-- [Differentiator](#differentiator)
-- [Integrator](#integrator)
+- [Transient Responses](#transient-responses)
+- [FIR Filter Design In Pinescript](#fir-filter-design-in-pinescript)
+- [Gaussian FIR Filter](#gaussian-fir-filter)
+- [Windowed Sinc FIR Filter](#windowed-sinc-fir-filter)
+- [IIR Filter Design In Pinescript](#iir-filter-design-in-pinescript)
+- [Butterworth IIR Filter](#butterworth-iir-filter)
+- [Gaussian IIR Filter](#gaussian-iir-filter)
+- [Rolling Signal To Noise Ratio](#rolling-signal-to-noise-ratio)
+- [Rolling Noise Factor](#rolling-noise-factor)
+- [Generating White Noise](#generating-white-noise)
+- [Estimating Signals Period](#estimating-signals-period)
+- [Tips And Tricks](#tips-and-tricks)
+- [References](#references)
+- [About The Author](#about-the-author)
+
+
## Introduction
-[Pine](https://www.tradingview.com/pine-script-docs/en/v4/Introduction.html) is a really lightweight scripting language but it still allows for the computation of basic signal processing processes. In this guide, basic techniques and tools used in signal processing are showcased alongside their implementation in Pine. It is recommended to know the basics of Pine before reading this article. Start [here](http://www.pinecoders.com/learning_pine_roadmap/) if you don't.
+[Pinescript](https://www.tradingview.com/pine-script-docs/en/v4/Introduction.html) is a really lightweight scripting language but it still allow for the computation of basic signal processing processes. In this guide, basic techniques and tools used in signal processing are showcased alongside their implementation in Pinescript. It is recommended to know the basics of Pinescript before reading this article. Start [here](http://www.pinecoders.com/learning_pine_roadmap/) if you don't.
+
+> Note that this guide is not intended to be an introduction to digital signal processing, even if some short definitions are shared.
+
+
## Digital Signals
-A digital signal is simply a sequence of values expressing a quantity that varies with time. When using Pine, you'll mostly be processing market prices as your main signal. However it is possible to process/generate a wide variety of digital signals with Pine.
+A digital signal is simply a sequence of values (*samples*) expressing a quantity that varies with time. When using Pinescript, you'll mostly be processing market prices as your main signal. However it is possible to process/generate a wide variety of digital signals with Pinescript.
+
+
### Periodic Signals
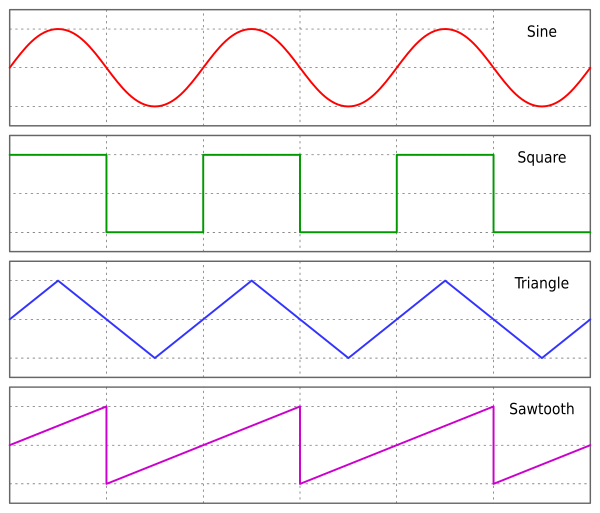
A periodic signal is a signal that repeats itself after some time. The image below shows a few different periodic signals:
- +
+ +
+
-Periodic signals possess characteristics such as **cycles**, **period**, **frequency** and **amplitude**. The **cycles** are the number of times the signal repeat himself, the **period** represents the duration of one cycle, the **frequency** is the number of cycles made by the signal in one unit of time and is calculated as the reciprocal of the **period** or `1/period`, and finally the amplitude is the highest absolute value of the signal.
+Periodic signals possess characteristics such as : **frequency**, **period**, **amplitude** and **phase**. The **frequency** is the number of cycles made by the signal per samples, the **period** represents the duration in samples of one cycle and is the reciprocal of the frequency ``1/frequency``, the amplitude is the highest absolute value of the signal and finally the **phase** is related to the position of the signal in the cycle, the phase is commonly expressed in degrees/radians.
+
+
-### Generating Periodic Signals
+#### Sine Wave
-The simplest periodic signal is the **sine wave** and is computed in Pine as follows:
+The simplest periodic signal is the sine wave, with function computed in Pinescript as follows:
```
-//@version=4
-//-----
-study("Sine Wave")
-pi = 3.14159
-n = bar_index
-period = 20
-amplitude = 1
-sin = sin(2*pi*1/period*n)*amplitude
-//---- Plot
-plot(sin, color=color.blue)
+sinewave(period,amplitude,phase)=>
+ pi = 3.14159265359
+ ph = phase/360*period
+ n = bar_index-ph
+ sin(2*pi*n/period)*amplitude
```
> As a reminder, `bar_index` is defined as the current number of `close` data points and is just a linear series of values equal to 0, 1, 2, 3, ...
-Other common periodic signals are:
+
-The **triangular wave** computed in Pine is as follows:
+#### Triangular Wave
+
+A triangular wave function is computed in Pinescript is as follows:
+
+```
+triangle(period,amplitude,phase)=>
+ pi = 3.14159265359
+ ph = phase/360*period
+ n = bar_index-ph
+ 2/pi*asin(sin(2*pi*n/period))*amplitude
+```
+
+
+#### Square Wave
+
+A square wave function is computed in Pinescript is as follows:
+
+```
+square(period,amplitude,phase)=>
+ pi = 3.14159265359
+ ph = phase/360*period
+ n = bar_index-ph
+ sign(sin(2*pi*n/period))*amplitude
+```
+
+> `sign(x)` is the signum function and output `1` when `x > 0` and `-1` when `x < 0`.
+
+
+
+#### Sawtooth Wave
+
+A sawtooth wave function is computed in Pinescript is as follows:
+
+```
+saw(period,amplitude,phase)=>
+ pi = 3.14159265359
+ ph = phase/360*period
+ n = bar_index-ph
+ 2/pi*atan(tan(2*pi*n/(2*period)))*amplitude
+```
+
+or:
+
+```
+saw(period,amplitude)=>
+ n = bar_index
+ saw = n%period/period*amplitude
+ (saw-.5)*2
+```
+
+This would output a linearly increasing sawtooth, this is why such wave is sometimes called sawtooth-up , a sawtooth-down wave can simply be made by multiplying the sawtooth-up wave by -1, that is `amplitude = -1`.
+
+ > Note that alternatives calculations exist in order to compute those signals. Here trigonometric forms are mostly used as they allow to change the phase of the signal.
+
+
+
+### Transient Signals
+
+Transient signals are signals that show a sudden change in their values, they are extremely important and commonly used signals when it comes to study the characteristics of discrete systems.
+
+> systems are defined as processes that take an input and return an output.
+
+
+
+#### Unit Impulse
+
+The first transient signal presented is the **unit impulse**. An unit impulse is simply a signal equal to 0 except at one point where it is equal to 1. The unit impulse is made from the unit impulse function, also called Dirac delta function denoted *δ(x)* and output 1 when *x* = 0 and 0 otherwise.
+
+
+ +
+
+
+
+
+The unit impulse is computed as follows:
```
-//@version=4
-study("Triangular Wave")
-//-----
-pi = 3.14159
n = bar_index
-period = 20
-amplitude = 1
-triangle = acos(sin(2*pi*1/period*n)*amplitude)
-//---- Plot
-plot(triangle, color=color.blue)
+impulse = n == 0 ? 1 : 0
```
-The **square wave** computed in Pine is as follows:
+A more convenient alternative would be the Kronecker delta function who can define the position in time of the impulse, that is the Kronecker delta function is just a shifted Dirac delta function. The Kronecker delta is computed as follows:
```
-//@version=4
-//-----
-study("Square Wave")
-pi = 3.14159
n = bar_index
-period = 20
-amplitude = 1
-square = sign(sin(2*pi*1/period*n))*amplitude
-//---- Plot
-plot(square, color=color.blue)
+impulse = n == k ? 1 : 0
```
-> `sign(x)` is the signum function and yields `1` when `x > 0` and `-1` when `x < 0`.
+where ``k`` is the position in time of the impulse.
+
+
+#### Unit Step
+
+Another commonly used transient signal is the **unit step signal** calculated from the unit step function also called Heavyside step function.
+
+
+ +
+
+
+
-The **sawtooth wave** computed in Pine is as follows:
+The unit step is computed as follows:
```
-//@version=4
-study("Sawtooth Wave")
-//-----
n = bar_index
-period = 20
-amplitude = 1
-saw = (((n/period)%1 - .5)*2)*amplitude
-//---- Plot
-plot(saw, color=color.blue)
+step = n >= 0 ? 1 : 0
```
-> `%` represents the modulo which is the remaining of a division and is not related to percentage here.
+However this would simply be like using `step = 1`, as ``bar_index`` does not have negative values. Therefore we can define the position of the step by using :
- > Note that those are not the only ways to compute those signals.
+```
+n = bar_index
+step = n >= k ? 1 : 0
+```
-## Cross Correlation
+An unit step is simply the cumulative sum of an unit impulse, that is ``step = cum(impulse)`` and therefore an unit impulse is the 1st difference of an unit step, that is ``impulse = change(step)``.
-Cross correlation measures the similarity between two signals, preferably stationary with mean ≈ 0. The cross correlation between signals `f` and `g` is often denoted by `f★g`. In Pine, cross correlation can be calculated as follows: `cum(f*g,length)` and the the running cross correlation of period `length` as `sum(f*g,length)`.
+
## Convolution
-Convolution is one of the most important concepts in signal processing. Basically, convolution is a combination of two signals to make a third signal. The convolution
-is mathematically denoted by the symbol `*`, not to be confused with the multiplication symbol in programming.
+Convolution is one of the most important concepts in signal processing. Basically, convolution is a combination of two signals that output a third signal. The convolution is mathematically denoted by the symbol `*`, not to be confused with the multiplication symbol in programming.
-For example the convolution of a signal `f` and another signal `g` is denoted `f*g`, in Pine this is done as follows:
+
+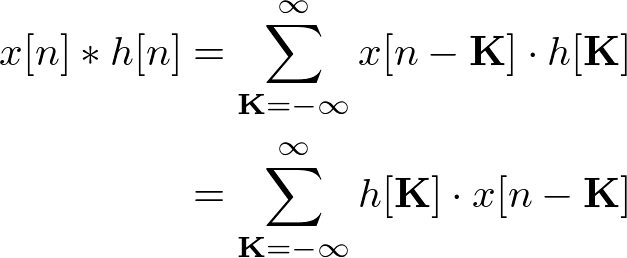 +
+
+
+
-```
-length = input(14)
-//-----
-convolve = sum(f*g,length)
-```
-Or alternatively:
+One can think of convolution as a sliding dot-product, or alternatively as a weighted rolling sum. In Pinescript convolution would be computed as follows :
```
-length = input(14)
-//-----
-convolve = 0
+sum = 0.
for i = 0 to length-1
- convolve := convolve + f[i]*g[i]
+ sum := x[i]*h[i]
```
-It can be seen that convolution is similar to a dot-product. In digital signal processing, convolution is what is used to create certain filters.
+which in this case is equivalent to ``sum(x*h,length)``. Certain moving averages are made by using convolution.
+
-## Impulse Function And Impulse Response
-An impulse function represents a series of values equal to 0, except at one point in time where the value is equal to 1. We can make an impulse function in Pine with the following code:
+## Transient Responses
+
+The transient response of a system is the output of a system using a transient signal as input. Two common types of transient responses are the **impulse response** and **step response**.
+
+
+
+### Impulse Response
+
+As its name suggest the impulse response of a system is the output of a system using an unit impulse as input. If a system convolve a signal with an unit impulse the impulse response will be equal to the original signal. The impulse response of a system is computed as follows:
```
-//@version=4
-study("Impulse")
-length = input(100)
-//-----
n = bar_index
-impulse = n == length ? 1 : 0
-//---- Plot
-plot(impulse, color=color.blue)
+impulse = n == k ? 1 : 0
+response = f(impulse)
```
-where the impulse is equal to 1 when `n` is equal to `length`.
-
-The impulse response of a system is a system using an impulse function as its input. The impulse response of a filter is the filter output using an impulse function as its input.
+Where ``f`` denote a system function. For example the impulse response of a simple moving average would be ``sma(impulse,length)``.
+
-## Step Function And Step Response
+### Step Response
-The step function, also called *heavy-side step function*, represents a series of values equal to 0 and then to 1 for the rest of the time. The step function is the cumulative sum of the impulse function `step = cum(impulse)` (therefore the impulse function is the differentiation of the step function or `impulse = change(step)`). In Pine we can make a step function by using:
+The step response of a system is the output of a system using an unit step as input. The step response of a system is computed as follows:
```
-//@version=4
-study("Step")
-length = input(100)
-//-----
n = bar_index
-step = n > length ? 1 : 0
-//---- Plot
-plot(step, color=color.blue)
+step = n >= k ? 1 : 0
+response = f(impulse)
```
-where the step is equal to 1 when `n` is greater than `length`.
-The step response of a system is a system using a step function as input. The step response of a filter is the filter output using a step function as input.
+The step response of a simple moving average would be ``sma(step,length)``.
-## FIR Filter Design In Pine
+
-Because Pine allows for convolution it is possible to design a wide variety of FIR filters. A filter `filter(input)` is equal to `input * filter(impulse)` where `*` denotes convolution, or more simply a filter output using a certain input is the convolution between the input and the filter impulse response.
+### Impulse-Step Response Equivalence
-In Pine you can make filters using:
+As said in the transient signals section, the cumulative sum of an unit impulse give an unit step, this is also true for their response, that is the step response of a system is the cumulative sum of the system impulse response and the impulse response of a system is the 1st difference of the system step response.
+
+```
+ImpulseResponse = change(f(step))
+
+StepResponse = cum(f(impulse))
+```
+
+This is extremely useful if one want to use both impulse and step response in a same script as it allow to only have an unit impulse instead of an unit impulse + a unit step in the script, and it avoid using a system twice, which can be extremely inefficient. In case one only want to switch from the impulse response to the step response it is easier to just replace ``n == k ? 1 : 0`` with ``n > k ? 1 : 0``.
+
+
+
+## FIR Filter Design In Pinescript
+
+
+![\sum_{i=0}^{P-1} x[n-i]h[i]](http://www.sciweavers.org/tex2img.php?eq=%5Csum_%7Bi%3D0%7D%5E%7BP-1%7D%20x%5Bn-i%5Dh%5Bi%5D&bc=Transparent&fc=Black&im=jpg&fs=36&ff=modern&edit=0) +
+
+
+
+
+Filters allow us to modify the frequency content of a signal (*see Fourier transform/decomposition*) by removing/attenuating unwanted frequencies from the input signal, certain filters can also amplify certain frequencies in the signal.
+
+FIR filters are a class of filters that are calculated by using convolution. "FIR" stand for "finite impulse response", which means that the filter impulse response will go back to *steady-state*, that is to 0 and will remain equal to 0. Because Pinescript can perform convolution it is possible to design a wide variety of FIR filters.
+
+A FIR filter `filter(input)` is equal to `input * filter(impulse)` where `*` denote convolution, more simply put a filter output using a certain input is the convolution between the input and the filter impulse response.
+
+In Pinescript you can make FIR filters by using:
```
filter(input) =>
sum = 0.
- for i = 1 to length
- sum := sum + input[i-1] * w[i-1]
+ for i = 0 to length-1
+ sum := sum + input[i] * h[i]
sum
```
-where `w[i-1]` are the filter coefficients (or *filter kernel*). Note that the sum of `w` must add up to 1 (this is called *total unity*). It is more convenient for `w` to be expressed as a function `w(x)`.
+where `length` is the filter length, and will often control the filtering amount. `h[i]` are the filter coefficients (also called *weights*), a term used to describe an entire set of coefficients is "kernel". However in Pinescript `h` will mostly denote an operation or a function of `i`.
+
+The coefficients fully describe the time domain properties of the filter, such as smoothness and lag, and can give hints on the filter properties in the frequency domain, however when we want to know how the filter interact with the frequency content of the signal we look at its **frequency response**, which for FIR filters is the Fourier transform of the impulse response.
+
+There exist several types of filters that modify the frequency content of an input signal in different ways, each one of them will be introduced in this section and we will learn how to create them in Pinescript.
+
+
+
+
+### FIR Low-Pass Filters Design
+
+
+ +
+
+
+
+
+Low-pass filters are used to remove/attenuate higher frequencies of an input signal, which lead to a smooth output. In technical analysis moving averages are low-pass filters. The simplest low-pass filter is the simple (arithmetic) moving average, which convolve the input signal with a constant, that is the filter coefficients of a simple moving average are all equal to ``1/length`` where ``length`` is the filter length. In Pinescript the most efficient way to compute a simple moving average is by using the built-in `sma` function.
+
+The simple moving average using convolution is computed as follows:
+
+```
+ma = 0.
+for i = 0 to length-1
+ ma := ma + input[i] * 1/length
+```
+
+Note however that in a loop, we repeat each operations `n` times where `n` is the number of loops, therefore if a loop is required, it is wiser to instead use :
+
+```
+sum = 0.
+for i = 0 to length-1
+ sum := sum + input[i]
+ma = sum/length
+```
+
+The sum of the coefficients of a low-pass filters must be equal to 1, this allow to have passband unity, if the sum of the coefficients is greater than 1 the filter passband will be superior to 1, which will give an output greater than the input signal, however if the sum of the coefficients is inferior to 1 and superior to 0 then the output will be lower than the input signal. The coefficients of a simple moving average already add-up to 1, but what if we use other coefficients that does not ? In this case we must normalize the convolution with the sum of the coefficients (*sometimes called normalizing constant*). This is done in pine as follows :
+
+```
+sum = 0.,sumh = 0.
+for i = 0 to length-1
+ h = sin(i/length)
+ sumh := sumh + h
+ sum := sum + input[i]*h
+lpfilter = sum/sumh
+```
+
+Here the sum of `h` is not equal to 1, however because we divide the convolution output by the sum of the coefficients (*`sumh` in the script*) we can get the filter with an unit passband.
+
+It is not possible to design FIR filters precisely with Pinescript, as the necessary tools are not available, however since the characteristics of a filter are described by its coefficients, we can roughly get an idea on how a FIR filter might process an input signal. Below is a short guide on the relationship between filter characteristics and filter coefficients.
+
+* A filter will be smooth if its impulse response is relatively symmetrical, with mostly positive values, and not to width nor to sharp. Width impulses responses will return an output similar to a simple moving average while sharp impulse responses will return an approximation of an impulse and the filter could just return a shifted version of the input signal.
+
+* The lag of a filter depends on the coefficients attributed to the current and past inputs of the signal, a filter attributing the highest coefficients to more recent input values will have a lower lag than a filter attributing the highest coefficients to oldest input values.
+
+* Lag is drastically reduced when the coefficients of the filter include negative values, this is because negative coefficients would amplify frequencies in the filter passband. Input values receiving negative coefficients should be the oldest ones, and the sum of the positive coefficients should be greater than the absolute sum of negative coefficients.
+
+* If a function `f(x)` is equal to 0 when `x = 1`, then using it as filter kernel would leave an unit passband, there would be no need to normalize the convolution.
+
+We can easily create all the other types of filters by using low-pass filters, they are therefore extremely useful.
+
+
+
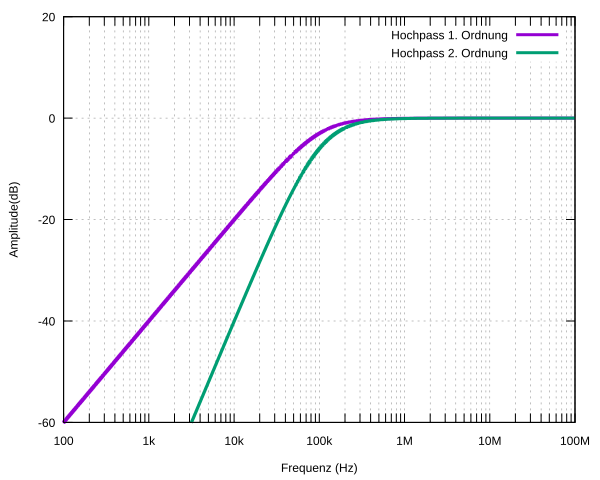
+### FIR High-Pass Filters Design
+
+
+ +
+
+
+
+
+High-pass filters are used to remove/attenuate lower frequencies of an input signal, they therefore perform the contrary operation of low-pass filters. The sum of the coefficients of an high-pass filter with passband unity is equal to 0 with most of the time a majority of negative coefficients.
+
+The easiest way to design high-pass filters by simply subtracting the input signal from a low-pass filter, therefore ``highpass = input - lowpass(input)``. For example the high-pass version of a simple moving average would be made as follows :
+
+```
+hpsma = input - sma(input,length)
+```
-When we can't have total unity (the sum of the coefficients doesn't add up to 1) we can rescale the convolution, which is done as follows:
+Another way of designing FIR high-pass filters is by modifying the coefficients of a low-pass filter by using a process called "spectral inversion", which consist in changing the sign of all the filter coefficients (*that is multiplying each coefficients by -1*) and by adding 1 to the first coefficient. For example spectral inversion using a simple moving average is done as follows:
```
-filter(input)=>
- a = 0.
- b = 0.
- for i = 1 to length
- w = sin(i/length)
- b := b + w
- a := a + input[i-1]*w
- a/b
+hpma = 0.
+for i = 0 to length-1
+ inv = 1/length * -1
+ h = i == 0 ? inv+1 : inv
+ hpma := hpma + input[i] * h
```
-Here `w` does not add to 1, however because we divide the convolution output by the sum of the coefficients (`b` in the script) we can get the filter without a problem.
+with `inv` representing the inverted coefficients, and with `h` adding 1 to the first inverted coefficient. Make sure the sum of the non inverted coefficients is equal to 1 in the first place.
+
+The impulse response of an high-pass filter is equal to `impulse - lowpass(impulse)` where `lowpass` is the low-pass version of the high-pass filter, and its step response is equal to 1 minus the step response of its low-pass version.
+
+
-You can also look at the following [template](https://www.tradingview.com/script/VttW3bJY-Template-For-Custom-FIR-Filters-Make-Your-Moving-Average/) which allows to design FIR filters.
+### FIR Band-Pass Filters Design
+
+
+ +
+
+
+
-### Simple Moving Average *(Boxcar)* Filter In Pine
+Band-pass filters are used to remove/attenuate lower and higher frequencies of an input signal, they therefore perform the operation of a low-pass and high-pass filters simultaneously. The sum of the coefficients of a band-pass filter with passband unity is like an high-pass filter equal to 0, however while most of the coefficients of an high-pass filters are negatives, band-pass filters possesses in general the same number of negative and positive coefficients.
-The simple (or *arithmetic*) moving average (*SMA*) sometimes called *boxcar filter* can be made in different ways with Pine. The standard and most efficient way is to use the built-in `sma(source,length)` function as follows:
+The easier way to design band-pass filters is by simply applying a low-pass filter to an high-pass filter, therefore ``bandpass = lowpass(highpass(input))``. For example the band-pass version of a simple moving average can be made as follows :
```
-//@version=4
-study("Sma",overlay=true)
-length = input(100)
-//-----
-Sma = sma(close,length)
-//---- Plot
-plot(Sma, color=color.blue)
+bpsma = sma(input - sma(input,length),length)
```
-This code plots the simple moving average of the closing price of period `length`.
-Another way is to use convolution with:
+Symmetrical signals in a range of [-1,1] are great choices of kernels for band-pass filters. Another option is to use the 1st difference `change` of a low-pass filter kernel in order to produce a band-pass filter kernel, in order to do so check the formula you are using to generate the coefficients of the low-pass filter, then get the formula derivative, this method mostly work with increasing/decreasing symmetrical kernels.
+The impulse response of a band-pass filter is equal to the convolution between the low-pass and high-pass impulses responses, that is: ``cum(lowpass(impulse)*highpass(impulse))``, and the step response would be equal to the cumulative sum of the band-pass filter impulse response.
+
+
+
+
+### FIR Band-Stop Filters Design
+
+
+ +
+
+
+
+
+
+Band-stop filters, also called band-reject or notch filters are used to remove/attenuate frequencies in a specific range of the input signal while preserving higher/lower frequencies, they therefore perform the contrary operation of band-pass filters. The sum of the coefficients of a band-stop filter with passband unity is equal to 1.
+
+The easiest way to design band-stop filters is by simply subtracting the input signal with a band-pass filter, therefore ``bandstop = input - bandpass(input)``. For example the band-stop version of a simple moving average can be made as follows :
+
+```
+bssma = input - sma(input - sma(input,length),length)
```
-//@version=4
-study("Sma",overlay=true)
-//-----
-Sma(input,length) =>
+
+Another way of designing FIR band-pass filters is by modifying the coefficients of a band-pass filter by using spectral inversion, which was used for designing FIR high-pass filters from a FIR low-pass filter kernel. For band-stop filter the process is the same, however we modify the coefficients of a FIR band-pass filter instead of a FIR low-pass filter.
+
+The impulse response of a band-stop filter is equal to `impulse + bandpass(impulse)` where `bandpass` is the band-pass version of the band-stop filter, and its step response is equal to 1 minus the step response of its band-pass version.
+
+
+
+### Windowing And Window Functions
+
+Windowing (*sometimes called "kernel tapering"*) is a process that allow to enhance the performance of a FIR filter in the frequency domain, for example windowing allow to remove ripples in the pass/stop-band of the filter frequency response, which allow a greater attenuation of frequencies thus creating a smoother output. Windowing can be used when the kernel of a FIR filter is non-periodic and/or has sharp borders (*which is the cause of ripples*), windowing would create a more periodic kernel and would attenuate or eliminate the sharp borders in it.
+
+Windowing simply consist in multiplying the filter kernel by a window function. In Pinescript, the general form of windowing would be done as follows :
+
+```
+filter(input) =>
sum = 0.
- for i = 1 to length
- sum := sum + input[i-1] * 1/length
+ for i = 0 to length-1
+ sum := sum + h[i]*w(i)*input[i]
sum
-//---- Plot
-plot(Sma(close,100), color=color.blue)
```
-`1/length` is the filter kernel of the simple moving average.
-An alternative way that allows a variable integer as the period can be made using the following code:
+where `w(i)` is a windowing function with argument `i`. There exist a wide variety of windowing function, which can also be used as kernels for low-pass filters, the most notable one will be described alongside their computations below.
+
+
+
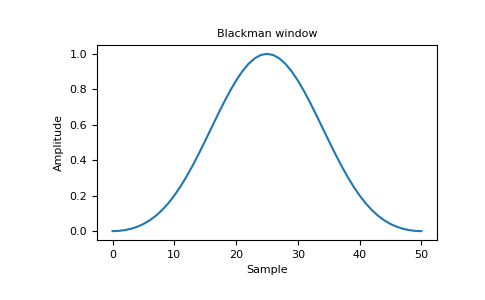
+#### Blackman Window
+
+
+ +
+
+
+The Blackman window is a window with a symmetrical shape consisting on the sum of 2 cosine waves. In Pinescript the function of a Blackman window can be computed follows:
```
-//@version=4
-study("Sma",overlay=true)
-//-----
-Sma(input,length) =>
- a = cum(input)
- (a - a[length])/length
-//---- Plot
-plot(Sma(close,100), color=color.blue)
+blackman(x) =>
+ pi = 3.14159
+ 0.42 - 0.5 * cos(2 * pi * x/(length-1)) + 0.08 * cos(4 * pi * x/(length-1))
```
-### Gaussian Filter
+Where `length` is the filter length.
+
+
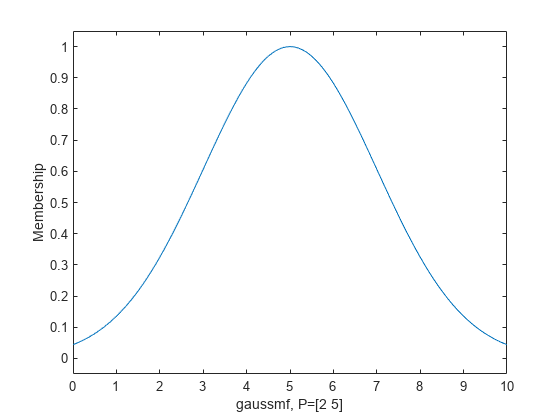
-The Gaussian filter is a filter with an impulse response equal to a Gaussian function:
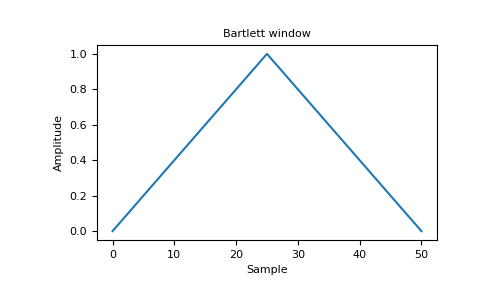
+#### Bartlett Window
- -
-
+ +
-The Gaussian function is calculated using the standard formula:
+The Bartlett window, also called triangular window is a window with a triangular shape. In Pinescript the function of a Bartlett window can be computed follows:
-
+
-The Gaussian function is calculated using the standard formula:
+The Bartlett window, also called triangular window is a window with a triangular shape. In Pinescript the function of a Bartlett window can be computed follows:
-
-
- -
-
-
+```
+bartlett(x) =>
+ pi = 3.14159
+ 1 - 2*abs(x - (length-1)/2)/(length-1)
+```
+
+The convolution between an input signal and a Bartlett function is the same as applying a simple moving average twice `sma(sma(...))`.
-with *b* = position of the peak and *c* = curve width. Pine can return an approximation of a Gaussian filter using the `alma(input, length, b, c)` function with `b` = 0.5.
+
-A Gaussian filter can also be made in Pine via convolution using the following code:
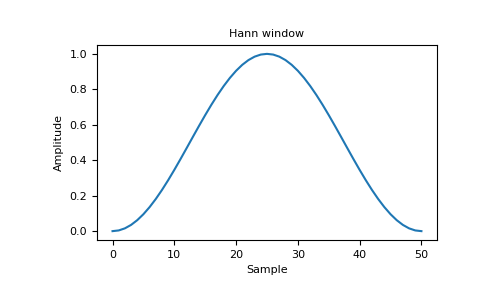
+#### Hann Window
+
+
+ +
+
+
+The Hann window, also called Hanning window is similar to the Blackman window but is wider. In Pinescript the function of an Hann window can be computed follows:
```
-//@version=4
-study("Gaussian Filter",overlay=true)
-//----
-gauss(input, length, width)=>
- a = 0.
- b = 0.
- for i = 1 to length
- w = exp(-pow(i/length - .5,2)/(2*pow(width,2)))
- b := b + w
- a := a + input[i-1]*w
- a/b
-//---- Plot
-plot(gauss(close, 100, 0.2), color=color.blue)
+hann(x) =>
+ pi = 3.14159
+ 0.5 - 0.5 * cos(2 * pi * x/(length-1))
```
-## Calculating Different Types Of Filters In Pine
+
-Filters comes in different types, where the type determines how the filter interacts with the frequency content of the signal.
+### Windowing Template
-### Low-Pass Filters
+In order to easily apply windowing to your FIR filter, you can use the following template who include all the previously seen windows.
-Low-pass filters are the most widely used type of filters. They remove high-frequency components—the noise—and thus smooth the signal. Most of the filtering functions integrated in Pine (`sma`, `wma`, `swma`, `alma`, etc.) are low-pass filters.
+```
+length = input(100),src = input(close)
+window = input("None",options=["Bartlett","Blackman","Hanning","None"])
+//----
+pi = 3.14159
+a(x) => 1 - 2*abs(x - (length-1)/2)/(length-1)
+b(x) => 0.42 - 0.5 * cos(2 * pi * x/(length-1)) + 0.08 * cos(4 * pi * x/(length-1))
+c(x) => 0.5 - 0.5 * cos(2 * pi * x/(length-1))
+//----
+f(x,y,z) => window == x ? y : z
+win(x) => f("Bartlett",a(x),f("Blackman",b(x),f("Hanning",c(x),1)))
+//----
+sumw = 0.,sum = 0.
+for i = 0 to length-1
+ h =
+ w = win(i)*h
+ sumw := sumw + w
+ sum := sum + src[i]*w
+filter = sum/sumw
+```
+
+here all you need to do is to put the calculation generating your filter coefficients in `h`.
-Low-pass filters posses the following frequency response:
+
+
+## Gaussian FIR Filter
- +
+ +
+
+
+A gaussian filter is a filter using a gaussian function as kernel, the gaussian function is characterized by its symmetrical bell shaped curve and has many properties that make the gaussian filter extremely useful in certain situations.
+
+The gaussian function is described by the following formula:
+
+
+
-When the filter's coefficients add up to 1, the filter is a low-pass filter.
+where σ is the standard deviation parameter and control the width of curve with lower values of σ making a wider curve. However a gaussian function is infinitely long and never reach 0, therefore using it as filter kernel is theoretically impossible, this is why the function is first truncated then used as filter kernel.
-### High-Pass Filters
+The simplest way to implement a gaussian filter is based on multiple applications of a simple moving average, the resulting impulse response would approximate a gaussian function, however this approach can be extremely inefficient. Another way is by using the function `alma(series, length, offset, sigma)` with `offset = 0.5`, however the filter impulse response is nonsymmetric when using an even filter length.
-High-pass filters remove low-frequency components of a signal, thus keeping higher-frequency components in the signal. They can be made by subtracting the input with the low-pass filter output: `highpass = input - lowpass(input)`. For example a simple moving average high-pass filter can be made in Pine as follows:
+A gaussian filter with symmetrical impulse response can be computed in Pinescript as follows:
```
-//@version=4
-study("Highpass SMA",overlay=true)
-length = input(14)
-//-----
-hp = close - sma(close,length)
-//---- Plot
-plot(hp, color=color.blue)
+length = input(100),src = input(close),width = input(2)
+//----
+sum = 0.,sumh = 0.
+for i = 0 to length-1
+ x = -length + 1 + i*2
+ h = exp(-.5*pow(width/length*x,2))
+ sumh := sumh + h
+ sum := sum + src[i] * h
+gauss = sum/sumh
```
-High-pass filters posses the following frequency response:
+
+
+
+## Windowed Sinc FIR Filter
- +
+ +
+
-When the filter's coefficients add up to 0, the filter is a high-pass filter.
+The windowed sinc filter is a filter that try to approximate an ideal frequency response, that is a filter who would only remove or keep frequencies in the signal, but would not attenuate them. A sinc filter use a sinc function as filter kernel, but like the gaussian filter, such function require to be infinite in order for the filter to return an ideal frequency response, since this is impossible with FIR filters the sinc function is truncated.
-### Band-Pass Filters
+In order to minimize the effects of truncation, windowing is applied (*the truncated sinc function is multiplied by a window function*), hence the name windowed sinc filter.
-Band-pass filters remove low/high-frequency components of a signal, thus keeping mid-frequency components in the signal. They can be made by applying a low-pass filter to an high-pass filter output: `bandpass = lowpass(highpass(input))`. For example a simple moving average band-pass filter can be made in Pine as follows:
+A windowed sinc filter with custom window is computed in Pinescript as follows:
```
-//@version=4
-study("Bandpass SMA",overlay=true)
-length = input(14)
-//-----
-bp = sma(close - sma(close,length),length)
-//---- Plot
-plot(bp, color=color.blue)
+length = input(100),src = input(close),cm = input(1,"Cut-Off Multiplier")
+window = input("None",options=["Bartlett","Blackman","Hanning","None"])
+//----
+pi = 3.14159
+a(x) => 1 - 2*abs(x - (length-1)/2)/(length-1)
+b(x) => 0.42 - 0.5 * cos(2 * pi * x/(length-1)) + 0.08 * cos(4 * pi * x/(length-1))
+c(x) => 0.5 - 0.5 * cos(2 * pi * x/(length-1))
+//----
+f(x,y,z) => window == x ? y : z
+win(x) => f("Bartlett",a(x),f("Blackman",b(x),f("Hanning",c(x),1)))
+//----
+cf = 1/length*cm
+sumw = 0.,sum = 0.
+for i = 0 to length-1
+ x = i - (length-1)/2
+ sinc = sin(2*pi*cf*x)/(pi*x)
+ w = nz(sinc,2*cf)*win(i)
+ sumw := sumw + w
+ sum := sum + src[i]*w
+filter = sum/sumw
```
-Band-pass filters posses the following frequency response:
+
+the cut-off multiplier `cm` determine the number of local maxima/minima in the sinc function, more precisely `n = 2*cm - 1` where `n` is the number of local maxima/minima.
+
+
+
+## IIR Filter Design In Pinescript
- +
+ +
+
-### Band-Stop Filters
+Unlike FIR filters who have an impulse response returning to steady state, IIR (*infinite impulse response*) filters have an infinitely long impulse response. IIR filters are also based on a weighted sum, however they use recursion, which means they use past outputs values as input. The use of recursion allow for extremely efficient filters, which was one of the downsides of FIR filters who require an high number of operations with larger filtering amounts (*higher `length`*), this is not the case with IIR filters.
+
+In Pinescript an IIR filter can be made as follows:
+
+```
+y = 0.
+y := b0*input+b1*input[1]...+a0*nz(y[1])+a1*nz(y[2])...
+```
+
+The coefficients that affect the input values (*all `b` in the code*) are called feed-forward coefficients, while the coefficients affecting past outputs values (*all `a` in the code*) are called feedback coefficients. The function `nz` output a user selected value (*0 by default*) when the input is `na`, therefore this function is useful at initializing the IIR filter, in general recursive inputs are initialized with 0, in this case we can rewrite the above code more efficiently with:
+
+```
+y = 0.
+y := a0*input+a1*input[1]...+nz(b0*y[1]+b1*y[2]...)
+```
+
+It is also common to use the input signal as initializing value.
+
+
+
+### Simple IIR Design Techniques
+
+Designing IIR filters is way more complicated than FIR ones, as the feed-forward and feedback coefficients needs to be precisely calculated in order to return a desired output. For an IIR low-pass filter with no overshoots, the sum of coefficients needs to be equal to 1 in order to have passband unity, however unlike FIR filters, if the sum of the IIR filter coefficients are greater than 1, the filter won't be stable. A simple way to make our IIR filter stable is by using a normalizing constant, for example:
+
+```
+b0 = 4,b1 = 5
+a0 = 9,a1 = 10
+norm = a0+a1+b0+b1
+
+y = 0.
+y := (b0*input+b1*input[1]+nz(a0*y[1]+a1*y[2]))/norm
+```
+
+Here the sum of the coefficients (*`norm` in the code*) is greater than 1, however since we divide the weighted sum by the sum of the coefficients we get our filter with passband unity. The simplest IIR low-pass filter is the exponential moving average (*sometimes called exponential filter*) and is equivalent to a simple moving average. In Pinescript an exponential moving average can be computed using the `ema` function, however we can also compute it as follows:
+
+```
+ema = 0.
+alpha = 2/(length+1)
+ema := alpha*input+(1-alpha)*nz(ema[1],src)
+```
-Band-stop filters remove mid-frequency components of a signal, thus keeping low/high-frequency components in the signal. They can be made by subtracting a band-pass filter output from an input: `bandstop = input - bandpass`. For example, a simple moving average band-stop filter can be made in Pine as follows:
+where `length` is greater than 1 and defined by the user. Higher values of `length` give a greater weight to the past output, thus making the filter return a smoother output, therefore feedback coefficients higher than the feed-forward coefficients will return a larger filtering amount. Here no normalizing constant are needed, as `alpha + (1-alpha) = 1`. Another way to compute an exponential moving average is done as follows:
```
-//@version=4
-study("Bandstop SMA",overlay=true)
-length = input(14)
-//-----
-bs = close - sma(close - sma(close,length),length)
-//---- Plot
-plot(bs, color=color.blue)
+ema = 0.
+alpha = 2/(length+1)
+ema := nz(ema[1],src) + alpha*nz(src-ema[1])
```
-Band-stop filters posses the following frequency response:
+
+Making different types of IIR filters can be done like previously mentioned in the FIR filter section, that is:
+
+* `IIR_highpass = input - IIR_lowpass(input)`
+* `IIR_bandpass = IIR_lowpass(IIR_highpass))`
+* `IIR_bandreject = input - IIR_bandpass`
+
+All you need is the low-pass filter.
+
+
+
+## Butterworth IIR Filter
- +
+ +
+
-## Exponential Averager
+The Butterworth filter is extremely popular because of its high frequency domain performances, the filter has no overshoots/undershoots and has a flat magnitude response. Some Butterworth filters with a different number of poles where described by Elhers [1] and are already available in the Pinescript repository.
+
+Alarcon, Guy and Binnie also proposed a simple 3 poles Butterworth filter [2], their design is computed in Pinescript as follows:
+
+```
+length = input(14),src = input(close)
+//----
+cf = 2*tan(2*3.14159*(1/length)/2)
+a0 = 8 + 8*cf + 4*pow(cf,2) + pow(cf,3)
+a1 = -24 - 8*cf + 4*pow(cf,2) + 3*pow(cf,3)
+a2 = 24 - 8*cf - 4*pow(cf,2) + 3*pow(cf,3)
+a3 = -8 + 8*cf - 4*pow(cf,2) + pow(cf,3)
+//----
+c = pow(cf,3)/a0
+d0 = -a1/a0
+d1 = -a2/a0
+d2 = -a3/a0
+//----
+out = 0.
+out := nz(c*(src + src[3]) + 3*c*(src[1] + src[2]) + d0*out[1] + d1*out[2] + d2*out[3],src)
+```
+
+
+
+## Gaussian IIR Filter
-The exponential averager (also known as *exponential moving average*, *leaky integrator* or *single exponential smoothing*) is a widely used recursive filter. This filter is similar to the simple moving average but its computation is way more efficient. This filter has the following form: `output = α*input+(1-α)*output[1]`.
+Many recursive implementations of the Gaussian filter exists and are way more efficient than their FIR counterparts. Unfortunately, they rely on forward-backward filtering in order to provide a symmetrical gaussian impulse response, this technique is not possible in Pinescript. Some alternatives exist, the most notable one being the Gaussian filter described by Elhers [3], which is based on the multiple applications of exponential moving averages, this filter is available in the Pinescript repository.
-In Pine we can use the integrated function `ema(input,length)` where `α = 2/(length+1)`, or:
+
+
+
+## Rolling Signal To Noise Ratio
+
+The signal to noise ratio (SNR) is used to measure the level of a signal relative to the level of unwanted noise, with a SNR inferior to 1 indicating more noise than signal. This metric is often expressed as the ratio of the mean and the standard deviation, however a rolling version might result more useful to the user, the signal to noise ratio function can be computed in Pinescript as follows :
```
-ea(input,alpha)=>
- s = 0.
- s := alpha * input + (1-alpha) * nz(s[1],close)
+snr(input) => sma(input,length)/stdev(input,length)
```
-with `1 > alpha > 0`.
+
-## Matched Filter
+## Rolling Noise Factor
-A matched filter is a system that maximizes the signal to noise ratio of the output. The impulse response of those filters are equal to the reversed input. Since Pine allows a variable index, we can build such filters using the following code:
+The noise factor is measurement that make use of the previously described signal to noise ratio and is defined as the ratio between the SNR of an input signal and the SNR of a system output. The rolling noise factor of a simple moving average can be computed in Pinescript as follows :
```
-filter(x,y) =>
- sum = 0.
- w = 0.
- for i = 0 to length-1
- w := w + y[length-i-1]
- sum := sum + x[i] * y[length-i-1]
- sum/w
+ma = sma(input,length)
+snrin = snr(input)
+snrout = snr(ma)
+nf = snrin/snrout
+```
+
+
+
+## Generating White Noise
+
+White noise is a type of random signal that has a constant power spectral density with no auto-correlation. Randomness can't be programmed, and therefore we can only use pseudo-random number generators in order to approximate white noise. A white noise generator function with uniform distribution and 0 mean can be computed in Pinescript as follows :
+
+```
+lcg(seed) =>
+ s = n < 10000 ? na : (171 * nz(s[1],seed))%30269
+ (s/30269 - .5)*2
+```
+
+where `seed` is a user defined number. This generator is the classical linear congruential generator with no increment. In the case where we want normally distributed white noise we simply need to sum various white noise signal with an uniform distribution, that is:
+
+```
+normal = lcg(1) + lcg(2) + lcg(3) + ...
+```
+
+
+
+## Estimating Signals Period
+
+### Periodic Signals
+
+The main property of any periodic signal is that `signal[n] == signal[n+period]`, we can use this property in order to find the period of a periodic signal.
+
+```
+period(input,range)=>
+ p = range+1
+ for i = 1 to range
+ p := input == input[i] ? min(i,p) : p
+```
+
+where `range` is defined by the user. This function would find the period of a periodic signal and would return `range+1` if `range` is to small, this function can also test if a signal is periodic.
+
+### Non Periodic Signals
+
+It is possible to estimate the lowest period of a signal even if the signal is not perfectly periodic and without searching in a specific range of periods, this method is therefore faster than the previous one.
+
+```
+period(input)=>
+ k = abs(change(sign(change(input))))/2
+ round(bar_index*2/cum(k))
+```
+
+
+
+## Tips And Tricks
+
+* Using `2*input - input[length/2]` as input for a low-pass filter with length `length` would reduce the filter lag.
+
+* Using linear combinations of low-pass filters allow to reduce lag, for example:
+```
+k*lowpass(input,length/2) - (k-1)*lowpass(input,length)`
```
+with higher values of `k` further minimizing the filter lag.
-where `x` is the input and `y` the signal of interest.
+* The derivative of sigmoid functions (*S shaped curves*) can be used as filter kernel in order to create really smooth filters.
-## Differentiator
+* The derivative of a symmetrical bell shaped curve can be used as filter kernel in order to create band-pass filters.
-The first difference differentiator is the simplest of all differentiators and consists in subtracting the previous input value from the current one. In Pine this can be done with `diff = input - input[1]` or `change(input)`.
+* If a script use a lot of simple moving averages, replace them with exponentially weighted ones as they are more efficient to compute.
-## Integrator
+* A strategy using IIR filters should start after the filter transient (*the first values of the filter*)
-The rectangular integrator is simply a running summation which can be made in Pine with the `cum(signal)` function, or:
+* A simple moving average can be computed more efficiently using the following code:
+```
+sma = change(cum(input),length)/length
+```
+* The difference between 2 filters can produce a band-pass filter as long as the first filter to be subtracted is more reactive than the other, for example:
```
-a = 0.
-a := nz(a[1],input) + input
+bandpass = sma(input,length/2) - sma(input,length)
+```
+
+* Measuring how spread out an input is from its low-pass filter can easily computed by using the naïve standard deviation.
```
+dev = sqrt(filter(input*input) - pow(filter(input),2))
+```
+
+A filter having negative coefficients (*or low-lag in general*) can produce `na` values.
+
+
+
+
+
+## References
+
+[1] Ehlers, J. F. "POLES, ZEROS, and HIGHER ORDER FILTERS." http://www.stockspotter.com/Files/polesandzeros.pdf
+
+[2] Alarcon, G., C. N. Guy, and C. D. Binnie. "A simple algorithm for a digital three-pole Butterworth filter of arbitrary cut-off frequency: application to digital electroencephalography." Journal of Neuroscience Methods 104.1 (2000): 35-44.
+
+[3] Ehlers, J. F. "Gaussian and Other Low Lag Filters" https://www.mesasoftware.com/papers/GaussianFilters.pdf
+
+
+
+## About The Author
+
+
+ +
+
+
+
+
+*alexgrover is a member of the tradingview community specialized in the creation of technical trading tools using the Pinescript scripting language. As a DSP enthusiast, he try to explain many DSP concepts in an intuitive way to the tradingview community.*
+
+*Thanks for reading ⊂( ・ω・)⊃*
-For examples of DSP techniques used in Pine scripts, see my indicators [here](https://www.tradingview.com/u/alexgrover/#published-scripts).
+
**[Back to top](#table-of-contents)**
 +
+ +
+
 ](http://pinecoders.com)
+[
](http://pinecoders.com)
+[ ](http://pinecoders.com)
-# Digital Signal Processing In Pine, by [Alex Grover](https://www.tradingview.com/u/alexgrover/#published-scripts)
+# Digital Signal Processing In Pinescript, by [Alex Grover](https://www.tradingview.com/u/alexgrover/#published-scripts)
-## Table of Contents
+
](http://pinecoders.com)
-# Digital Signal Processing In Pine, by [Alex Grover](https://www.tradingview.com/u/alexgrover/#published-scripts)
+# Digital Signal Processing In Pinescript, by [Alex Grover](https://www.tradingview.com/u/alexgrover/#published-scripts)
-## Table of Contents
+ +
+ +
+
 +
+
+
+ +
+
+
+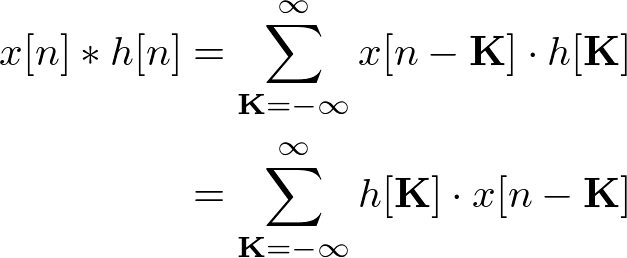 +
+
+
+
+
+
 +
+
+
+ +
+
+
+ +
+
+
+ +
+
+
+ +
+ -
- +
-The Gaussian function is calculated using the standard formula:
+The Bartlett window, also called triangular window is a window with a triangular shape. In Pinescript the function of a Bartlett window can be computed follows:
-
+
-The Gaussian function is calculated using the standard formula:
+The Bartlett window, also called triangular window is a window with a triangular shape. In Pinescript the function of a Bartlett window can be computed follows:
-
 +
+ +
+ +
+
 +
+ +
+
 +
+ +
+
 +
+
 +
+