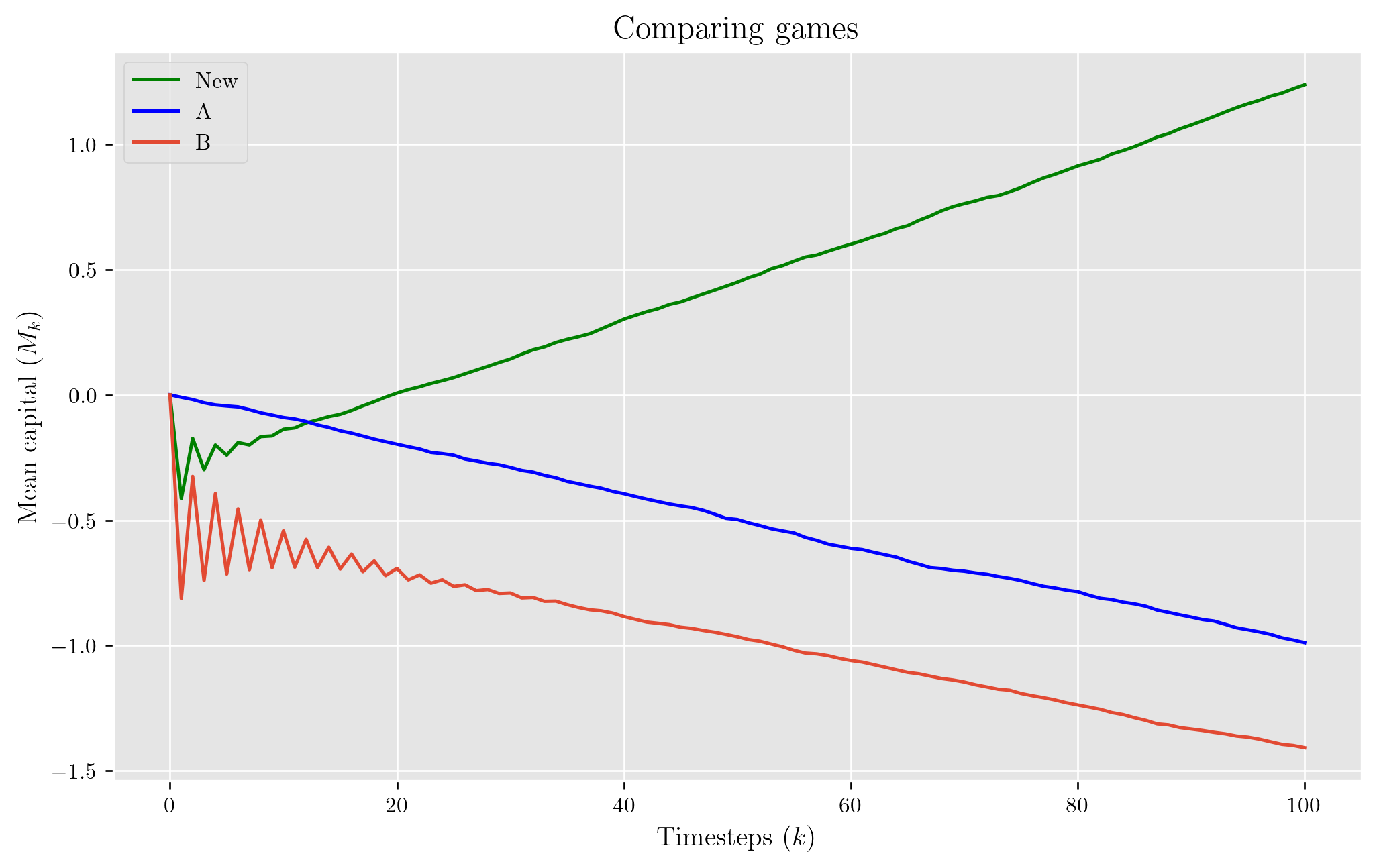
Can two wrongs be right? The plot below is a demonstration of how two stochastic processes have negative drifts separately, but a random combination of those two leads to a drift which is positive! This is known as Parrondo's paradox.
This GitHub repository contains Monte Carlo simulations resulting in above plot and coding solutions to all the other interesting probability puzzles in the book 'Digital Dice' by Paul J. Nahin. The author describes 21 problems based on "everyday real life." The solutions to these problems are implemented here in Python 3.
The large part of the book is available on Google Books. The text descriptions of the problems in the Jupyter notebooks are directly taken from the book and often modified slightly to keep them concise.
Much of the heavylifting in the codes provided here is performed by NumPy's random module. One of the notebooks uses Pandas to organize the outputs. The plots are done using Matplotlib. Finally, since some Monte Carlo simulations take numerous iterations to converge, we utilize a progress-bar to keep track of the loop index. This is done using the slick tqdm package. Please ensure you have these packages installed before running the Jupyter notebooks here.
Installation instructions for tqdm can be found here.
(Right: Cropped image from the statue of Secretion-Urge by Tony Cragg.)