DenMune: A density-peak clustering algorithm

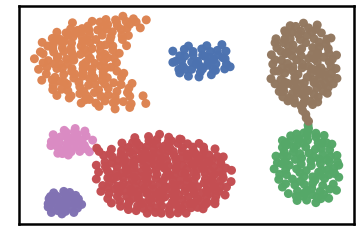
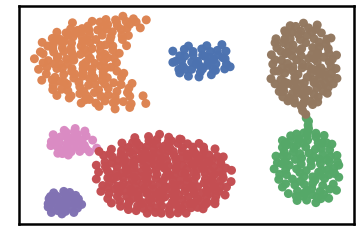
DenMune a clustering algorithm that can find clusters of arbitrary size, shapes and densities in two-dimensions. Higher dimensions are first reduced to 2-D using the t-sne. The algorithm relies on a single parameter K (the number of nearest neighbors). The results show the superiority of the algorithm. Enjoy the simplicity but the power of DenMune.

Based on the paper

Paper	Journal
Mohamed Abbas, Adel El-Zoghabi, Amin Ahoukry,
DenMune: Density peak based clustering using mutual nearest neighbors
In: Journal of Pattern Recognition, Elsevier,
volume 109, number 107589, January 2021
DOI: https://doi.org/10.1016/j.patcog.2020.107589

Documentation:

Documentation, including tutorials, are available on https://denmune.readthedocs.io

Watch it in action

This 30 seconds will tell you how a density-baased algorithm, DenMune propagates:

When less means more

Most calssic clustering algorithms fail in detecting complex clusters where clusters are of different size, shape, density, and being exist in noisy data. Recently, a density-based algorithm named DenMune showed great ability in detecting complex shapes even in noisy data. it can detect number of clusters automatically, detect both pre-identified-noise and post-identified-noise automatically and removing them.

It can achieve accuracy reach 100% in most classic pattern problems, achieve 97% in MNIST dataset. A great advantage of this algorithm is being single-parameter algorithm. All you need is to set number of k-nearest neighbor and the algorithm will care about the rest. Being Non-senstive to changes in k, make it robust and stable.

Keep in mind, the algorithm reduce any N-D dataset to only 2-D dataset initially, so it is a good benefit of this algorithm is being always to plot your data and explore it which make this algorithm a good candidate for data exploration. Finally, the algorithm comes with neat package for visualizing data, validating it and analyze the whole clustering process.

How to install DenMune

Simply install DenMune clustering algorithm using pip command from the official Python repository

From the shell run the command

pip install denmune

From jupyter notebook cell run the command

!pip install denmune

How to use DenMune

Once DenMune is installed, you just need to import it

from denmune import DenMune

Please note that first denmune (the package) in small letters, while the other one(the class itself) has D and M in capital case.

Read data

There are four possible cases of data:

• only train data without labels
• only labeld train data
• labeled train data in addition to test data without labels
• labeled train data in addition to labeled test data

#=============================================
# First scenario: train data without labels 
# ============================================

data_path = 'datasets/denmune/chameleon/'  
dataset = "t7.10k.csv" 
data_file = data_path + dataset 

# train data without labels
X_train = pd.read_csv(data_file, sep=',', header=None)

knn = 39 # k-nearest neighbor, the only parameter required by the algorithm

dm = DenMune(train_data=X_train, k_nearest=knn)
labels, validity = dm.fit_predict(show_analyzer=False, show_noise=True)

This is an intutive dataset which has no groundtruth provided

#=============================================
# Second scenario: train data with labels 
# ============================================

data_path = 'datasets/denmune/shapes/'  
dataset = "aggregation.csv"
data_file = data_path + dataset 

# train data with labels
X_train = pd.read_csv(data_file, sep=',', header=None)
y_train = X_train.iloc[:, -1]
X_train = X_train.drop(X_train.columns[-1], axis=1)  

knn = 6 # k-nearest neighbor, the only parameter required by the algorithm

dm = DenMune(train_data=X_train, train_truth= y_train, k_nearest=knn)
labels, validity = dm.fit_predict(show_analyzer=False, show_noise=True)

Datset groundtruth

Datset as detected by DenMune at k=6

#=================================================================
# Third scenario: train data with labels in addition to test data
# ================================================================

data_path = 'datasets/denmune/pendigits/'  
file_2d = data_path + 'pendigits-2d.csv'

# train data with labels 
X_train = pd.read_csv(data_path + 'train.csv', sep=',', header=None)
y_train = X_train.iloc[:, -1]
X_train = X_train.drop(X_train.columns[-1], axis=1)

# test data without labels
X_test = pd.read_csv(data_path + 'test.csv', sep=',', header=None) 
X_test = X_test.drop(X_test.columns[-1], axis=1)

knn = 50 # k-nearest neighbor, the only parameter required by the algorithm

dm = DenMune(train_data=X_train, train_truth= y_train,
             test_data= X_test, 
             k_nearest=knn)
labels, validity = dm.fit_predict(show_analyzer=True, show_noise=True)

dataset groundtruth

dataset as detected by DenMune at k=50

test data as predicted by DenMune on training the dataset at k=50

Algorithm's Parameters

1. Parameters used within the initialization of the DenMune class

def __init__ (self,
                  train_data=None, test_data=None,
                  train_truth=None, test_truth=None, 
                  file_2d =None, k_nearest=None, 
                  rgn_tsne=False, prop_step=0,
                  ):    

• train_data:

  • data used for training the algorithm
  • default: None. It should be provided by the use, otherwise an error will riase.

• train_truth:

  • labels of training data
  • default: None

• test_data:

  • data used for testing the algorithm

• test_truth:

  • labels of testing data
  • default: None

• k_nearest:

  • number of nearest neighbor
  • default: 0. the default is invalid. k-nearest neighbor should be at leat 1.

• rgn_tsn:

  • when set to True: It will regenerate the reduced 2-D version of the N-D dataset each time the algorithm run.
  • when set to False: It will generate the reduced 2-D version of the N-D dataset first time only, then will reuse the saved exist file
  • default: True

• file_2d: name (include location) of file used save/load the reduced 2-d version

  • if empty: the algorithm will create temporary file named '_temp_2d'
  • default: None

• prop_step:

  • size of increment used in showing the clustering propagation.
  • leave this parameter set to 0, the default value, unless you are willing intentionally to enter the propagation mode.
  • default: 0

2. Parameters used within the fit_predict function:

 def fit_predict(self,
                    validate=True,
                    show_plots=True,
                    show_noise=True, 
                    show_analyzer=True
                    ):

• validate:

  • validate data on/off according to five measures integrated with DenMUne (Accuracy. F1-score, NMI index, AMI index, ARI index)
  • default: True

• show_plots:

  • show/hide plotting of data
  • default: True

• show_noise:

  • show/hide noise and outlier
  • default: True

• show_analyzer:

  • show/hide the analyzer
  • default: True

The Analyzer

The algorithm provide an intutive tool called analyzer, once called it will provide you with in-depth analysis on how your clustering results perform.

Noise Detection

DenMune detects noise and outlier automatically, no need to any further work from your side.

• It plots pre-identified noise in black
• It plots post-identified noise in light grey

You can set show_noise parameter to False.

# let us show noise

m = DenMune(train_data=X_train, k_nearest=knn)
labels, validity = dm.fit_predict(show_noise=True)

# let us show clean data by removing noise

m = DenMune(train_data=X_train, k_nearest=knn)
labels, validity = dm.fit_predict(show_noise=False)

noisy data	clean data

Validatation

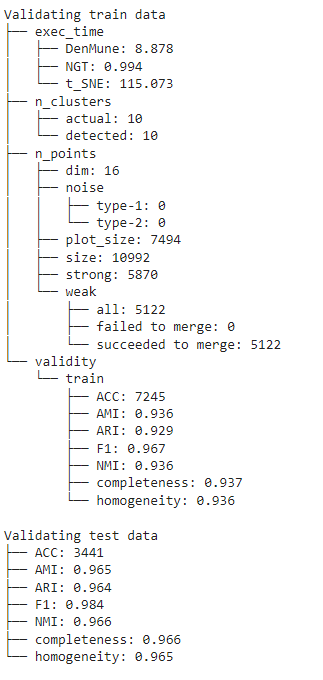
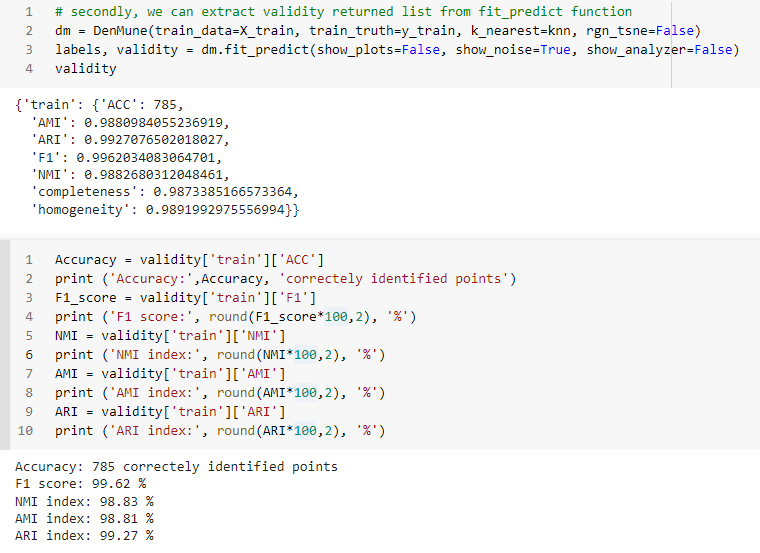
You can get your validation results using 3 methods

• by showing the Analyzer
• extract values from the validity returned list from fit_predict function
• extract values from the Analyzer dictionary

There are five validity measures built-in the algorithm, which are:

• ACC, Accuracy
• F1 score
• NMI index (Normalized Mutual Information)
• AMI index (Adjusted Mutual Information)
• ARI index (Adjusted Rand Index)

K-nearest Evolution

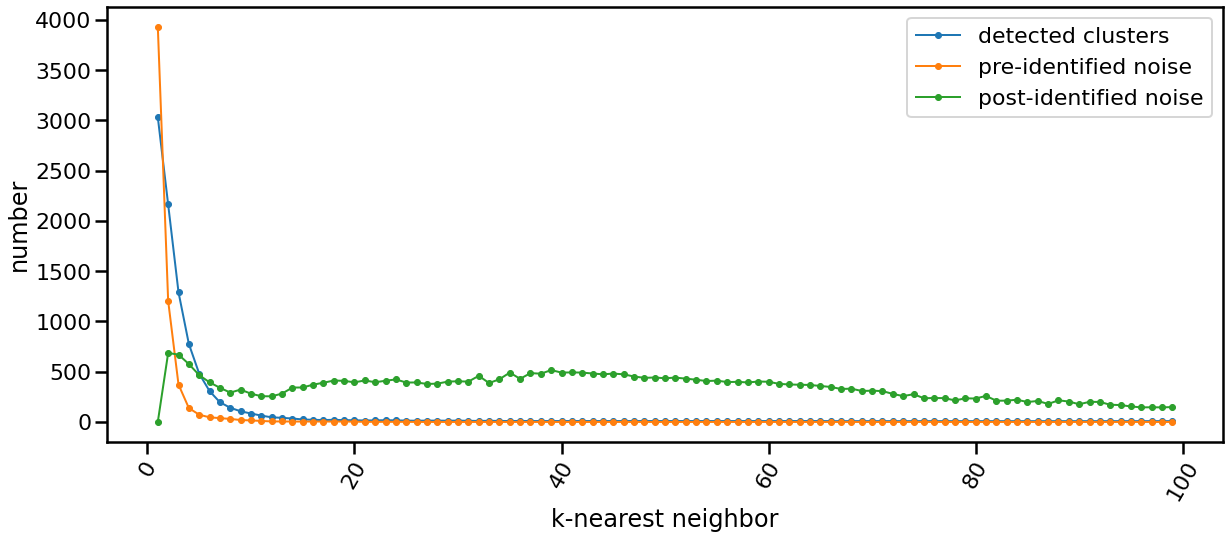
The following chart shows the evolution of pre and post identified noise in correspondence to increase of number of knn. Also, detected number of clusters is analyzed in the same chart in relation with both types of identified noise.

The Scalability

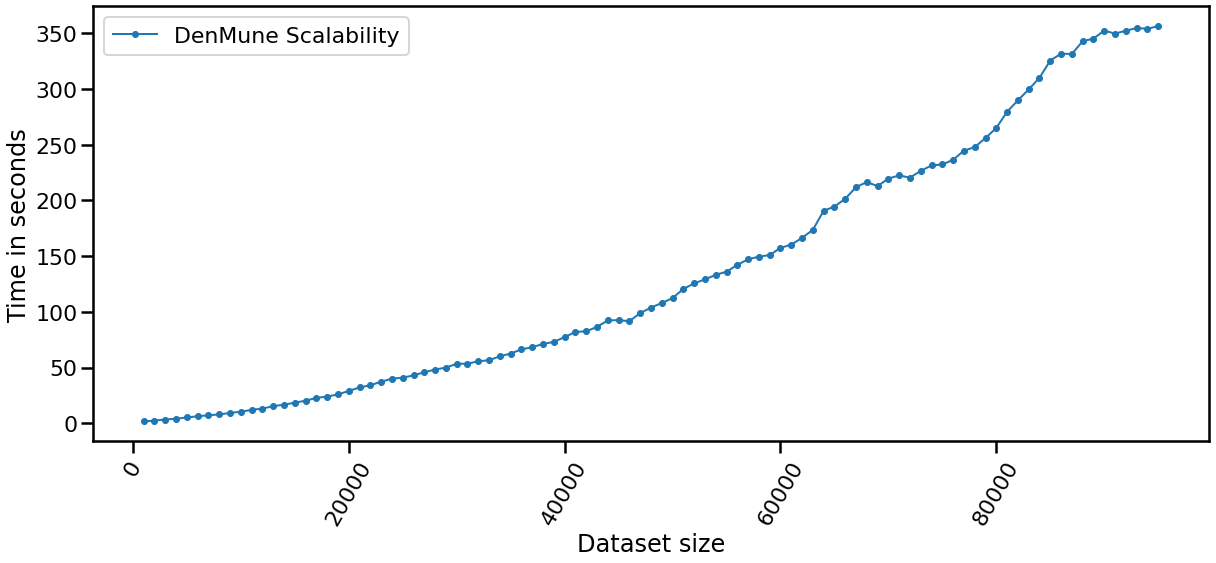
data size	time
data size: 5000	time: 2.3139 seconds
data size: 10000	time: 5.8752 seconds
data size: 15000	time: 12.4535 seconds
data size: 20000	time: 18.8466 seconds
data size: 25000	time: 28.992 seconds
data size: 30000	time: 39.3166 seconds
data size: 35000	time: 39.4842 seconds
data size: 40000	time: 63.7649 seconds
data size: 45000	time: 73.6828 seconds
data size: 50000	time: 86.9194 seconds
data size: 55000	time: 90.1077 seconds
data size: 60000	time: 125.0228 seconds
data size: 65000	time: 149.1858 seconds
data size: 70000	time: 177.4184 seconds
data size: 75000	time: 204.0712 seconds
data size: 80000	time: 220.502 seconds
data size: 85000	time: 251.7625 seconds
data size: 100000	time: 257.563 seconds

|

The Stability

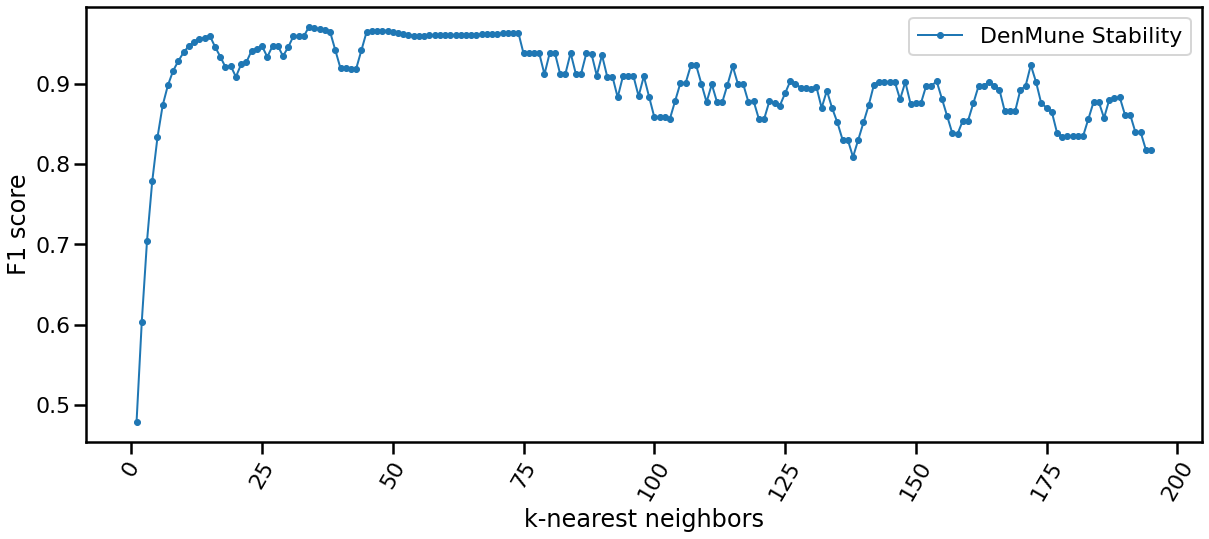
The algorithm is only single-parameter, even more it not sensitive to changes in that parameter, k. You may guess that from the following chart yourself. This is of greate benfit for you as a data exploration analyst. You can simply explore the dataset using an arbitrary k. Being Non-senstive to changes in k, make it robust and stable.

Reveal the propagation

one of the top performing feature in this algorithm is enabling you to watch how your clusters propagate to construct the final output clusters. just use the parameter 'prop_step' as in the following example:

dataset = "t7.10k" #
data_path = 'datasets/denmune/chameleon/' 

# train file
data_file = data_path + dataset +'.csv'
X_train = pd.read_csv(data_file, sep=',', header=None)


from itertools import chain

# Denmune's Paramaters
knn = 39 # number of k-nearest neighbor, the only parameter required by the algorithm

# create list of differnt snapshots of the propagation
snapshots = chain(range(2,5), range(5,50,10), range(50, 100, 25), range(100,500,100), range(500,2000, 250), range(1000,5500, 500))

from IPython.display import clear_output
for snapshot in snapshots:
    print ("itration", snapshot )
    clear_output(wait=True)
    dm = DenMune(train_data=X_train, k_nearest=knn, rgn_tsne=False, prop_step=snapshot)
    labels, validity = dm.fit_predict(show_analyzer=False, show_noise=False)  

Interact with the algorithm

This notebook allows you interact with the algorithm in many asspects:

• you can choose which dataset to cluster (among 4 chameleon datasets)
• you can decide which number of k-nearest neighbor to use
• show noise on/off; thus you can invesitigate noise detected by the algorithm
• show analyzer on/off

How to run and test

1. Launch Examples in Repo2Docker Binder

   Simply use our repo2docker offered by mybinder.org, which encapsulate the algorithm and all required data in one virtual machine instance. All jupter notebooks examples found in this repository will be also available to you in action to practice in this respo2docer. Thanks mybinder.org, you made it possible!

   

2. Launch each Example in Kaggle workspace

   If you are a kaggler like me, then Kaggle, the best workspace where data scientist meet, should fit you to test the algorithm with great experince.

   Dataset	Kaggle URL
   When less means more - kaggle
   Non-groundtruth datasets - kaggle
   2D Shape datasets - kaggle
   MNIST dataset kaggle
   Iris dataset kaggle
   Training MNIST to get 97%
   Noise detection - kaggle
   Validation - kaggle
   The beauty of propagation - kaggle
   The beauty of propagation part2 - kaggle
   Snapshots of propagation -kaggle
   Scalability kaggle
   Stability - kaggle
   k-nearest-evolution - kaggle

3. Launch each Example in Google Research, CoLab

   Need to test examples one by one, then here another option. Use colab offered by google research to test each example individually.

   Here is a list of Google CoLab URL to use the algorithm interactively

   Dataset	CoLab URL
   How to use it - colab
   Chameleon datasets - colab
   2D Shape datasets - colab
   MNIST dataset - colab
   iris dataset - colab
   Get 97% by training MNIST dataset - colab
   Non-groundtruth datasets - colab
   Noise detection - colab
   Validation - colab
   How it propagates - colab
   Snapshots of propagation - colab
   Scalability - colab
   Stability vs number of nearest neighbors - colab
   k-nearest-evolution - colab

How to cite

If you have used this codebase in a scientific publication and wish to cite it, please use the Journal of Pattern Recognition article

Mohamed Abbas McInnes, Adel El-Zoghaby, Amin Ahoukry, *DenMune: Density peak based clustering using mutual nearest neighbors*
In: Journal of Pattern Recognition, Elsevier, volume 109, number 107589.
January 2021

@article{ABBAS2021107589,
title = {DenMune: Density peak based clustering using mutual nearest neighbors},
journal = {Pattern Recognition},
volume = {109},
pages = {107589},
year = {2021},
issn = {0031-3203},
doi = {https://doi.org/10.1016/j.patcog.2020.107589},
url = {https://www.sciencedirect.com/science/article/pii/S0031320320303927},
author = {Mohamed Abbas and Adel El-Zoghabi and Amin Shoukry},
keywords = {Clustering, Mutual neighbors, Dimensionality reduction, Arbitrary shapes, Pattern recognition, Nearest neighbors, Density peak},
abstract = {Many clustering algorithms fail when clusters are of arbitrary shapes, of varying densities, or the data classes are unbalanced and close to each other, even in two dimensions. A novel clustering algorithm “DenMune” is presented to meet this challenge. It is based on identifying dense regions using mutual nearest neighborhoods of size K, where K is the only parameter required from the user, besides obeying the mutual nearest neighbor consistency principle. The algorithm is stable for a wide range of values of K. Moreover, it is able to automatically detect and remove noise from the clustering process as well as detecting the target clusters. It produces robust results on various low and high dimensional datasets relative to several known state of the art clustering algorithms.}
}

Licensing

The DenMune algorithm is 3-clause BSD licensed. Enjoy.

Task List

• Update Github with the DenMune sourcode
• create repo2docker repository
• Create pip Package
• create CoLab shared examples
• create documentation
• create Kaggle shared examples
• PEP8 compliant
• Continuous integration
• scikit-learn compatible
• Unit tests (coverage: 100%)
• create conda package