Skip to content

Commit d8ae23f

Browse files
jannikmaierhoeferjannikmaierhoefer
authored
docs: openai structured outputs added sdk parse helper (langfuse#767)
1 parent 6dae7df commit d8ae23f

File tree

5 files changed

+314
-53
lines changed

5 files changed

+314
-53
lines changed

‎cookbook/integration_openai_structured_output.ipynb

Lines changed: 136 additions & 21 deletions
Original file line numberDiff line numberDiff line change
@@ -67,7 +67,7 @@
6767
},
6868
{
6969
"cell_type": "code",
70-
"execution_count": 2,
70+
"execution_count": 4,
7171
"metadata": {
7272
"id": "79Cu3eLlEOCA"
7373
},
@@ -110,7 +110,7 @@
110110
},
111111
{
112112
"cell_type": "code",
113-
"execution_count": 3,
113+
"execution_count": 5,
114114
"metadata": {
115115
"id": "8IZjc893Ef1c"
116116
},
@@ -138,7 +138,7 @@
138138
},
139139
{
140140
"cell_type": "code",
141-
"execution_count": 4,
141+
"execution_count": 6,
142142
"metadata": {
143143
"id": "iKWRHCjVF55-"
144144
},
@@ -197,7 +197,7 @@
197197
},
198198
{
199199
"cell_type": "code",
200-
"execution_count": 5,
200+
"execution_count": 7,
201201
"metadata": {
202202
"colab": {
203203
"base_uri": "https://localhost:8080/"
@@ -210,7 +210,7 @@
210210
"name": "stdout",
211211
"output_type": "stream",
212212
"text": [
213-
"{\"steps\":[{\"explanation\":\"First, we need to isolate the term with the variable, 8x, by eliminating the constant term on the left-hand side. We do this by subtracting 7 from both sides of the equation.\",\"output\":\"8x + 7 - 7 = -23 - 7\"},{\"explanation\":\"After subtracting 7 from both sides, the equation simplifies to 8x = -30.\",\"output\":\"8x = -30\"},{\"explanation\":\"Next, to solve for x, we need to divide both sides of the equation by 8, the coefficient of x.\",\"output\":\"8x/8 = -30/8\"},{\"explanation\":\"Dividing each side by 8 gives us x = -30/8, which simplifies to x = -15/4. This is done by dividing both the numerator and the denominator by 2.\",\"output\":\"x = -15/4\"}],\"final_answer\":\"x = -15/4\"}\n"
213+
"{\"steps\":[{\"explanation\":\"We need to isolate the term with the variable, 8x. So, we start by subtracting 7 from both sides to remove the constant term on the left side.\",\"output\":\"8x + 7 - 7 = -23 - 7\"},{\"explanation\":\"The +7 and -7 on the left side cancel each other out, leaving us with 8x. The right side simplifies to -30.\",\"output\":\"8x = -30\"},{\"explanation\":\"To solve for x, divide both sides of the equation by 8, which is the coefficient of x.\",\"output\":\"x = -30 / 8\"},{\"explanation\":\"Simplify the fraction -30/8 by finding the greatest common divisor, which is 2.\",\"output\":\"x = -15 / 4\"}],\"final_answer\":\"x = -15/4\"}\n"
214214
]
215215
}
216216
],
@@ -225,7 +225,7 @@
225225
},
226226
{
227227
"cell_type": "code",
228-
"execution_count": null,
228+
"execution_count": 8,
229229
"metadata": {
230230
"colab": {
231231
"base_uri": "https://localhost:8080/",
@@ -234,24 +234,51 @@
234234
"id": "mAwEts-hCA73",
235235
"outputId": "9101c8ff-7b83-4ae6-f6c0-0da6a45ab251"
236236
},
237-
"outputs": [],
237+
"outputs": [
238+
{
239+
"name": "stdout",
240+
"output_type": "stream",
241+
"text": [
242+
"Step 1: We need to isolate the term with the variable, 8x. So, we start by subtracting 7 from both sides to remove the constant term on the left side.\n",
243+
"\n",
244+
"8x + 7 - 7 = -23 - 7\n",
245+
"\n",
246+
"\n",
247+
"Step 2: The +7 and -7 on the left side cancel each other out, leaving us with 8x. The right side simplifies to -30.\n",
248+
"\n",
249+
"8x = -30\n",
250+
"\n",
251+
"\n",
252+
"Step 3: To solve for x, divide both sides of the equation by 8, which is the coefficient of x.\n",
253+
"\n",
254+
"x = -30 / 8\n",
255+
"\n",
256+
"\n",
257+
"Step 4: Simplify the fraction -30/8 by finding the greatest common divisor, which is 2.\n",
258+
"\n",
259+
"x = -15 / 4\n",
260+
"\n",
261+
"\n",
262+
"Final answer:\n",
263+
"\n",
264+
"\n",
265+
"x = -15/4\n"
266+
]
267+
}
268+
],
238269
"source": [
239270
"# Print results step by step\n",
240-
"from IPython.display import Math, display\n",
241-
"\n",
242-
"def print_math_response(response):\n",
243-
" result = json.loads(response)\n",
244-
" steps = result['steps']\n",
245-
" final_answer = result['final_answer']\n",
246-
" for i in range(len(steps)):\n",
247-
" print(f\"Step {i+1}: {steps[i]['explanation']}\\n\")\n",
248-
" display(Math(steps[i]['output']))\n",
249-
" print(\"\\n\")\n",
250271
"\n",
251-
" print(\"Final answer:\\n\\n\")\n",
252-
" display(Math(final_answer))\n",
272+
"result = json.loads(result.content)\n",
273+
"steps = result['steps']\n",
274+
"final_answer = result['final_answer']\n",
275+
"for i in range(len(steps)):\n",
276+
" print(f\"Step {i+1}: {steps[i]['explanation']}\\n\")\n",
277+
" print(steps[i]['output'])\n",
278+
" print(\"\\n\")\n",
253279
"\n",
254-
"print_math_response(result.content)"
280+
"print(\"Final answer:\\n\\n\")\n",
281+
"print(final_answer)"
255282
]
256283
},
257284
{
@@ -276,6 +303,85 @@
276303
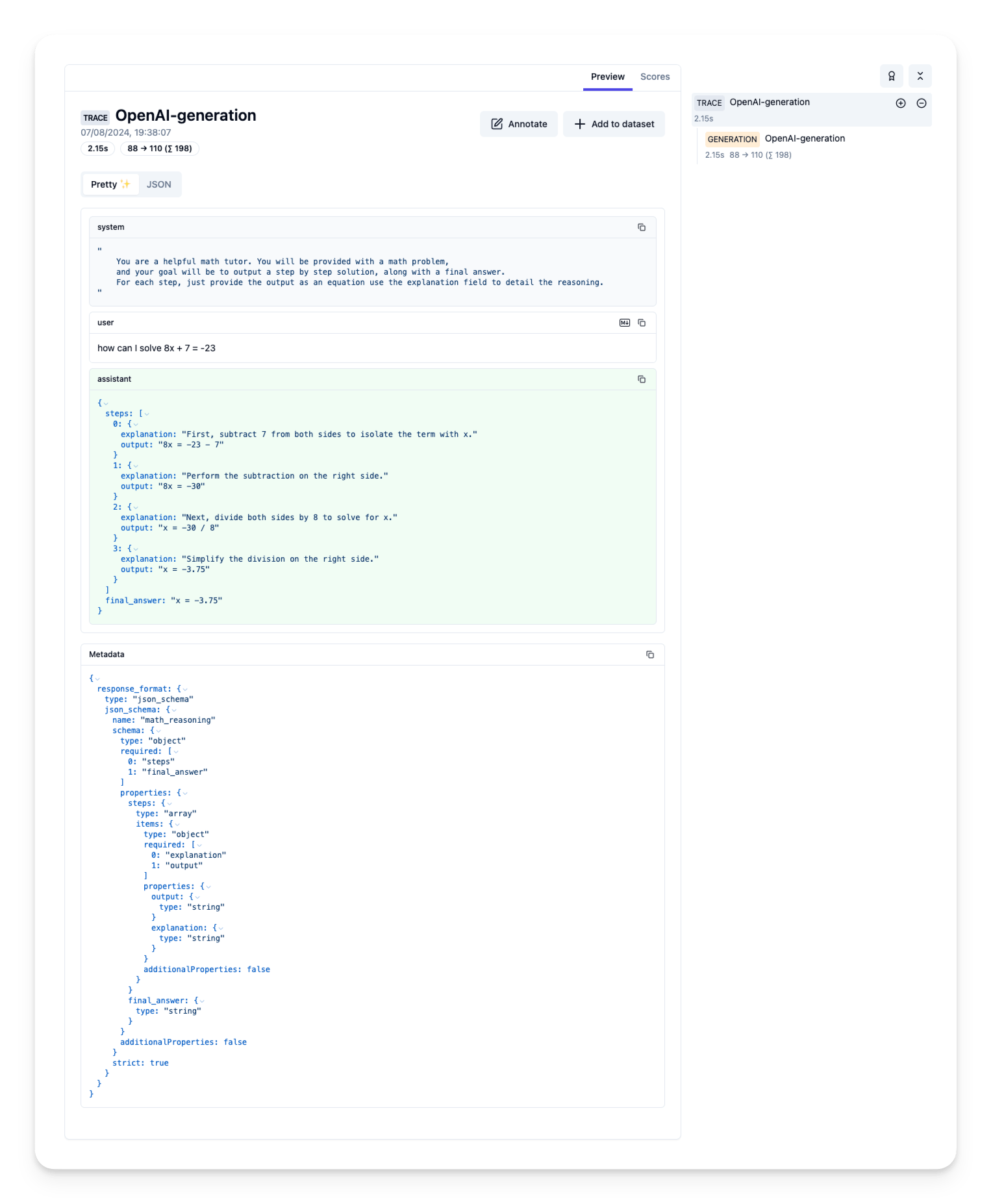"![View example trace in the Langfuse UI](https://langfuse.com/images/cookbook/integration-openai-structured-outputs-tracing.png)"
277304
]
278305
},
306+
{
307+
"cell_type": "markdown",
308+
"metadata": {},
309+
"source": [
310+
"## Alternative: Using the SDK `parse` helper\n",
311+
"\n",
312+
"The new SDK version adds a `parse` helper, allowing you to use your own Pydantic model without defining a JSON schema."
313+
]
314+
},
315+
{
316+
"cell_type": "code",
317+
"execution_count": 9,
318+
"metadata": {},
319+
"outputs": [],
320+
"source": [
321+
"from pydantic import BaseModel\n",
322+
"\n",
323+
"class MathReasoning(BaseModel):\n",
324+
" class Step(BaseModel):\n",
325+
" explanation: str\n",
326+
" output: str\n",
327+
"\n",
328+
" steps: list[Step]\n",
329+
" final_answer: str\n",
330+
"\n",
331+
"def get_math_solution(question: str):\n",
332+
" response = client.beta.chat.completions.parse(\n",
333+
" model=openai_model,\n",
334+
" messages=[\n",
335+
" {\"role\": \"system\", \"content\": math_tutor_prompt},\n",
336+
" {\"role\": \"user\", \"content\": question},\n",
337+
" ],\n",
338+
" response_format=MathReasoning,\n",
339+
" )\n",
340+
"\n",
341+
" return response.choices[0].message"
342+
]
343+
},
344+
{
345+
"cell_type": "code",
346+
"execution_count": 10,
347+
"metadata": {},
348+
"outputs": [
349+
{
350+
"name": "stdout",
351+
"output_type": "stream",
352+
"text": [
353+
"[Step(explanation='To isolate the term with the variable on one side of the equation, start by subtracting 7 from both sides.', output='8x = -23 - 7'), Step(explanation='Combine like terms on the right side to simplify the equation.', output='8x = -30'), Step(explanation='Divide both sides by 8 to solve for x.', output='x = -30 / 8'), Step(explanation='Simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 2.', output='x = -15 / 4')]\n",
354+
"Final answer:\n",
355+
"x = -15/4\n"
356+
]
357+
}
358+
],
359+
"source": [
360+
"result = get_math_solution(question).parsed\n",
361+
"\n",
362+
"print(result.steps)\n",
363+
"print(\"Final answer:\")\n",
364+
"print(result.final_answer)"
365+
]
366+
},
367+
{
368+
"cell_type": "markdown",
369+
"metadata": {},
370+
"source": [
371+
"## See your trace in Langfuse\n",
372+
"\n",
373+
"You can now see the trace and your supplied Pydantic model in Langfuse.\n",
374+
"\n",
375+
"[Example trace in Langfuse](https://cloud.langfuse.com/project/cloramnkj0002jz088vzn1ja4/traces/59c4376a-c8eb-4ecb-8780-2f028b87e7eb)"
376+
]
377+
},
378+
{
379+
"cell_type": "markdown",
380+
"metadata": {},
381+
"source": [
382+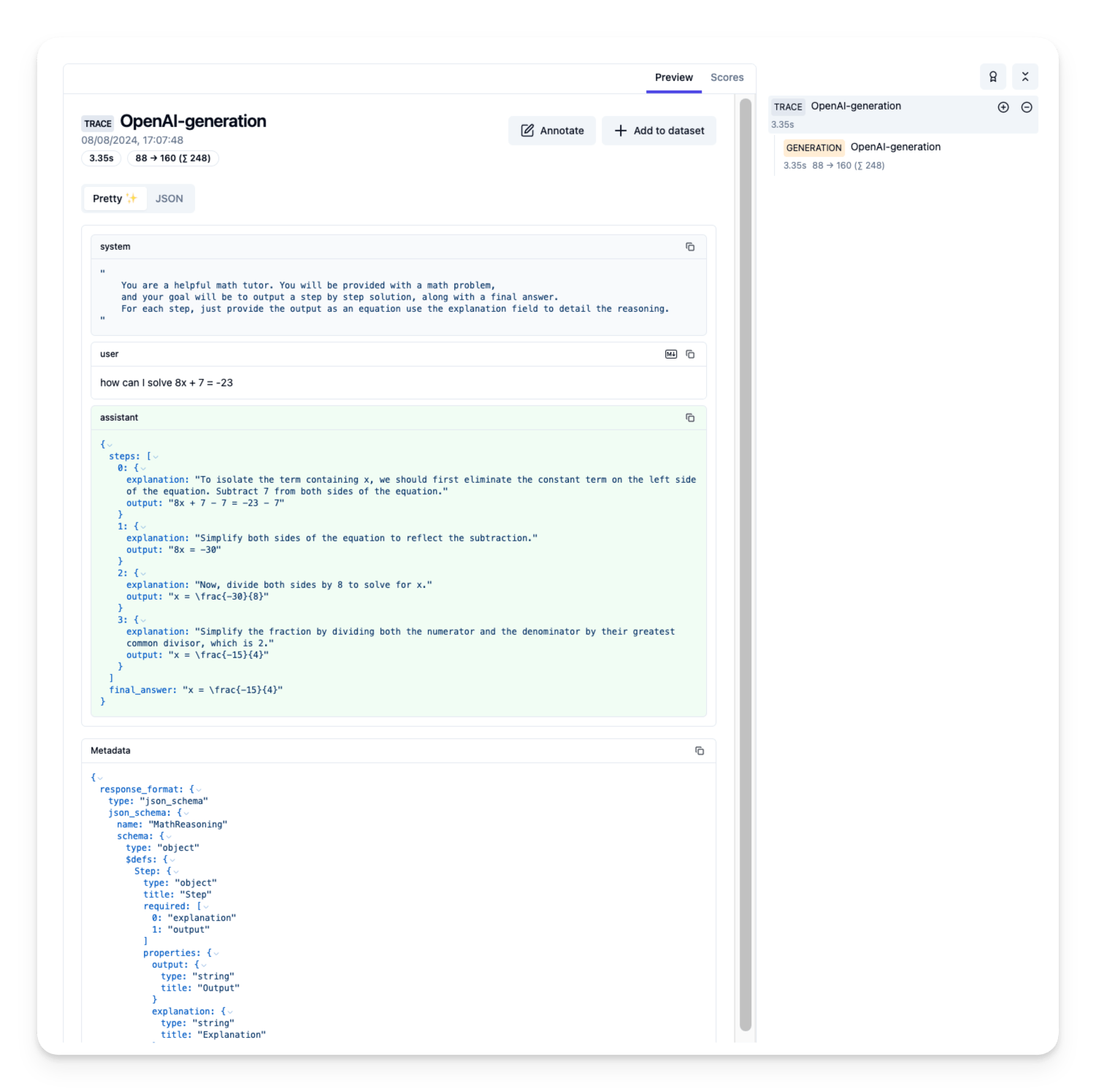
"![View example trace in the Langfuse UI](https://langfuse.com/images/cookbook/integration_openai_structured_outputs_tracing_parse.png)"
383+
]
384+
},
279385
{
280386
"cell_type": "markdown",
281387
"metadata": {
@@ -297,7 +403,16 @@
297403
"name": "python3"
298404
},
299405
"language_info": {
300-
"name": "python"
406+
"codemirror_mode": {
407+
"name": "ipython",
408+
"version": 3
409+
},
410+
"file_extension": ".py",
411+
"mimetype": "text/x-python",
412+
"name": "python",
413+
"nbconvert_exporter": "python",
414+
"pygments_lexer": "ipython3",
415+
"version": "3.9.18"
301416
}
302417
},
303418
"nbformat": 4,

‎pages/docs/integrations/openai/python/structured-outputs.md

Lines changed: 87 additions & 14 deletions
Original file line numberDiff line numberDiff line change
@@ -135,29 +135,51 @@ result = get_math_solution(question)
135135
print(result.content)
136136
```
137137

138-
{"steps":[{"explanation":"First, we need to isolate the term with the variable, 8x, by eliminating the constant term on the left-hand side. We do this by subtracting 7 from both sides of the equation.","output":"8x + 7 - 7 = -23 - 7"},{"explanation":"After subtracting 7 from both sides, the equation simplifies to 8x = -30.","output":"8x = -30"},{"explanation":"Next, to solve for x, we need to divide both sides of the equation by 8, the coefficient of x.","output":"8x/8 = -30/8"},{"explanation":"Dividing each side by 8 gives us x = -30/8, which simplifies to x = -15/4. This is done by dividing both the numerator and the denominator by 2.","output":"x = -15/4"}],"final_answer":"x = -15/4"}
138+
{"steps":[{"explanation":"We need to isolate the term with the variable, 8x. So, we start by subtracting 7 from both sides to remove the constant term on the left side.","output":"8x + 7 - 7 = -23 - 7"},{"explanation":"The +7 and -7 on the left side cancel each other out, leaving us with 8x. The right side simplifies to -30.","output":"8x = -30"},{"explanation":"To solve for x, divide both sides of the equation by 8, which is the coefficient of x.","output":"x = -30 / 8"},{"explanation":"Simplify the fraction -30/8 by finding the greatest common divisor, which is 2.","output":"x = -15 / 4"}],"final_answer":"x = -15/4"}
139139

140140

141141

142142
```python
143143
# Print results step by step
144-
from IPython.display import Math, display
145144

146-
def print_math_response(response):
147-
result = json.loads(response)
148-
steps = result['steps']
149-
final_answer = result['final_answer']
150-
for i in range(len(steps)):
151-
print(f"Step {i+1}: {steps[i]['explanation']}\n")
152-
display(Math(steps[i]['output']))
153-
print("\n")
145+
result = json.loads(result.content)
146+
steps = result['steps']
147+
final_answer = result['final_answer']
148+
for i in range(len(steps)):
149+
print(f"Step {i+1}: {steps[i]['explanation']}\n")
150+
print(steps[i]['output'])
151+
print("\n")
154152

155-
print("Final answer:\n\n")
156-
display(Math(final_answer))
157-
158-
print_math_response(result.content)
153+
print("Final answer:\n\n")
154+
print(final_answer)
159155
```
160156

157+
Step 1: We need to isolate the term with the variable, 8x. So, we start by subtracting 7 from both sides to remove the constant term on the left side.
158+
159+
8x + 7 - 7 = -23 - 7
160+
161+
162+
Step 2: The +7 and -7 on the left side cancel each other out, leaving us with 8x. The right side simplifies to -30.
163+
164+
8x = -30
165+
166+
167+
Step 3: To solve for x, divide both sides of the equation by 8, which is the coefficient of x.
168+
169+
x = -30 / 8
170+
171+
172+
Step 4: Simplify the fraction -30/8 by finding the greatest common divisor, which is 2.
173+
174+
x = -15 / 4
175+
176+
177+
Final answer:
178+
179+
180+
x = -15/4
181+
182+
161183
## Step 3: See your trace in Langfuse
162184

163185
You can now see the trace and the JSON schema in Langfuse.
@@ -166,6 +188,57 @@ You can now see the trace and the JSON schema in Langfuse.
166188

167189
![View example trace in the Langfuse UI](https://langfuse.com/images/cookbook/integration-openai-structured-outputs-tracing.png)
168190

191+
## Alternative: Using the SDK `parse` helper
192+
193+
The new SDK version adds a `parse` helper, allowing you to use your own Pydantic model without defining a JSON schema.
194+
195+
196+
```python
197+
from pydantic import BaseModel
198+
199+
class MathReasoning(BaseModel):
200+
class Step(BaseModel):
201+
explanation: str
202+
output: str
203+
204+
steps: list[Step]
205+
final_answer: str
206+
207+
def get_math_solution(question: str):
208+
response = client.beta.chat.completions.parse(
209+
model=openai_model,
210+
messages=[
211+
{"role": "system", "content": math_tutor_prompt},
212+
{"role": "user", "content": question},
213+
],
214+
response_format=MathReasoning,
215+
)
216+
217+
return response.choices[0].message
218+
```
219+
220+
221+
```python
222+
result = get_math_solution(question).parsed
223+
224+
print(result.steps)
225+
print("Final answer:")
226+
print(result.final_answer)
227+
```
228+
229+
[Step(explanation='To isolate the term with the variable on one side of the equation, start by subtracting 7 from both sides.', output='8x = -23 - 7'), Step(explanation='Combine like terms on the right side to simplify the equation.', output='8x = -30'), Step(explanation='Divide both sides by 8 to solve for x.', output='x = -30 / 8'), Step(explanation='Simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 2.', output='x = -15 / 4')]
230+
Final answer:
231+
x = -15/4
232+
233+
234+
## See your trace in Langfuse
235+
236+
You can now see the trace and your supplied Pydantic model in Langfuse.
237+
238+
[Example trace in Langfuse](https://cloud.langfuse.com/project/cloramnkj0002jz088vzn1ja4/traces/59c4376a-c8eb-4ecb-8780-2f028b87e7eb)
239+
240+
![View example trace in the Langfuse UI](https://langfuse.com/images/cookbook/integration_openai_structured_outputs_tracing_parse.png)
241+
169242
## Feedback
170243

171244
If you have any feedback or requests, please create a GitHub [Issue](https://langfuse.com/issue) or share your idea with the community on [Discord](https://langfuse.com/discord).

‎pages/docs/security/overview.mdx

Lines changed: 4 additions & 4 deletions
Original file line numberDiff line numberDiff line change
@@ -1,10 +1,10 @@
11
---
2-
description: Survey of common security problems facing LLM-based applications and how to use Langfuse to trace, prevent, and evaluate security risks.
2+
description: Survey of common security problems facing LLM-based applications and how to use Langfuse to trace, prevent, and evaluate LLM safety risks.
33
---
44

55
# Monitor LLM Security
66

7-
There are a host of potential security risks involved with LLM-based applications. These include prompt injection, leakage of personally identifiable information (PII), or harmful prompts. Langfuse can be used to monitor and protect against these security risks, and investigate incidents when they occur.
7+
There are a host of potential safety risks involved with LLM-based applications. These include prompt injection, leakage of personally identifiable information (PII), or harmful prompts. Langfuse can be used to monitor and protect against these security risks, and investigate incidents when they occur.
88

99
<CloudflareVideo
1010
videoId="3a89dd733399f0c9da4aa5ac9da80d78"
@@ -163,13 +163,13 @@ In this trace ([public link](https://cloud.langfuse.com/project/cloramnkj0002jz0
163163

164164
## Learn more
165165

166-
Find more examples in our cookbook.
166+
Find more examples of LLM security monitoring in our cookbook.
167167

168168
import { FileCode, BookOpen } from "lucide-react";
169169

170170
<Cards num={3}>
171171
<Card
172-
title="Coookbook"
172+
title="Coookbook: Observing LLM Security"
173173
href="/docs/security/example-python"
174174
icon={<FileCode />}
175175
/>

0 commit comments

Comments
 (0)