Đọc tài liệu này bằng ngôn ngữ khác: Tiếng Anh
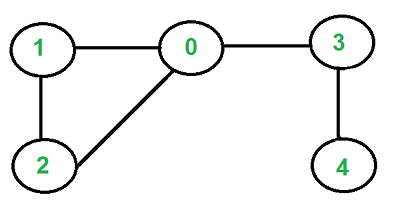
Trong lý thuyết đồ thị, một chu trình là một đường đi của các cạnh và đỉnh nơi mà một đỉnh có thể đạt được từ chính nó. Có một số loại chu trình khác nhau, chủ yếu là một đường đi kín và một chu trình đơn giản.
Một đường đi kín bao gồm một chuỗi các đỉnh bắt đầu và kết thúc tại cùng một đỉnh, với mỗi hai đỉnh liên tiếp trong chuỗi kề nhau trong đồ thị. Trong một đồ thị có hướng, mỗi cạnh phải được duyệt bởi đường đi một cách nhất quán với hướng của nó: cạnh phải được hướng từ đỉnh sớm hơn của hai đỉnh liên tiếp đến đỉnh sau của hai đỉnh trong chuỗi. Việc chọn đỉnh bắt đầu không quan trọng: việc duyệt cùng một chuỗi chu kỳ các cạnh từ các đỉnh bắt đầu khác nhau tạo ra cùng một đường đi kín.
Một chu trình đơn giản có thể được định nghĩa hoặc là một đường đi kín không cho phép lặp lại các đỉnh và cạnh, ngoại trừ việc lặp lại đỉnh bắt đầu và kết thúc, hoặc là tập hợp các cạnh trong một đường đi như vậy. Hai định nghĩa là tương đương trong đồ thị có hướng, nơi chu trình đơn giản cũng được gọi là chu trình có hướng: chuỗi chu kỳ các đỉnh và cạnh trong một đường đi hoàn toàn được xác định bởi tập hợp các cạnh mà nó sử dụng. Trong đồ thị không hướng, tập hợp các cạnh của một chu trình có thể được duyệt bởi một đường đi theo một trong hai hướng, tạo ra hai chu trình có hướng có thể cho mỗi chu trình không hướng. Một mạch có thể là một đường đi kín cho phép lặp lại các đỉnh nhưng không phải cạnh; tuy nhiên, nó cũng có thể là một chu trình đơn giản, vì vậy định nghĩa rõ ràng được khuyến nghị khi nó được sử dụng.
Một đồ thị với các cạnh được tô màu để minh họa đường đi H-A-B (màu xanh lá), đường đi kín hoặc
đường đi với một đỉnh lặp lại B-D-E-F-D-C-B (màu xanh dương) và một chu trình không lặp lại cạnh hoặc
đỉnh H-D-G-H (màu đỏ)
Thông tin chung:
Chu trình trong đồ thị không hướng:
- Phát hiện chu trình trong đồ thị không hướng trên GeeksForGeeks
- Thuật toán phát hiện chu trình trong đồ thị không hướng trên YouTube
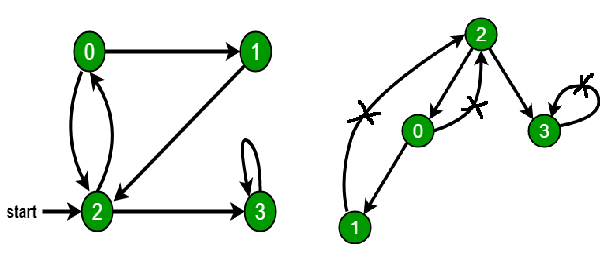
Chu trình trong đồ thị có hướng: