Nhấn vào đây để đọc bằng ngôn ngữ khác: English
Trong toán học, thuật toán Euclid, hay còn gọi là thuật toán của Euclid, là một phương pháp hiệu quả để tính ước số chung lớn nhất (GCD) của hai số, đó là số lớn nhất chia cả hai số đó mà không có phần dư.
Thuật toán Euclid dựa trên nguyên tắc rằng ước số chung lớn nhất
của hai số không thay đổi nếu số lớn hơn được thay thế bằng hiệu của nó
với số nhỏ hơn. Ví dụ, 21 là ước số chung lớn nhất của 252 và
105 (vì 252 = 21 × 12 và 105 = 21 × 5), và cũng là
số 21 là ước số chung lớn nhất của 105 và 252 − 105 = 147.
Khi quá trình thay thế này giảm số lớn hơn trong hai số đó,
lặp lại quá trình này cho đến khi hai số trở thành bằng nhau.
Khi điều đó xảy ra, chúng là ước số chung lớn nhất của hai số ban đầu.
Bằng cách đảo ngược các bước, ước số chung lớn nhất có thể được biểu diễn
dưới dạng tổng của hai số ban đầu mỗi số được nhân với một số nguyên
dương hoặc âm, ví dụ, 21 = 5 × 105 + (−2) × 252.
Việc rằng ước số chung lớn nhất luôn có thể được biểu diễn theo cách này được
biết đến với tên gọi là định lý Bézout.
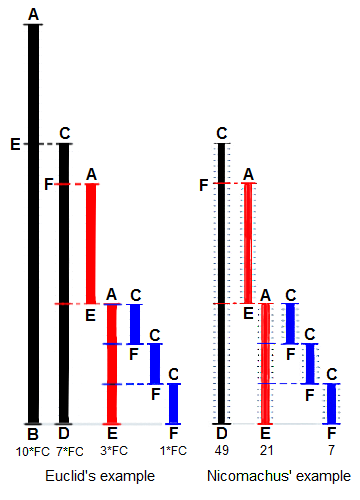
Phương pháp của Euclid để tìm ước số chung lớn nhất (GCD)
của hai độ dài ban đầu BA và DC, đều được định nghĩa là
bội số của một độ dài "đơn vị" chung. Độ dài DC ngắn hơn,
nó được sử dụng để "đo" BA, nhưng chỉ một lần vì
phần dư EA nhỏ hơn DC. EA bây giờ đo độ dài ngắn hơn DC (hai lần),
với phần dư FC còn ngắn hơn EA. Sau đó, FC đo độ dài EA (ba lần).
Bởi vì không có phần dư, quá trình kết thúc với FC là USCLN.
Bên phải là ví dụ của Nicomachus với các số 49 và 21,
kết quả là USCLN của chúng là 7 (được suy ra từ Heath 1908:300).
Một hình chữ nhật 24-by-60 được phủ bằng mười viên gạch vuông 12-by-12,
trong đó 12 là ước số chung lớn nhất của 24 và 60. Nói chung hơn,
một hình chữ nhật a-by-b có thể được phủ bằng các viên gạch vuông có cạnh
dài c chỉ khi c là ước số chung của a và b.
Hoạt hình dựa trên phép trừ của thuật toán Euclid.
Hình chữ nhật ban đầu có kích thước a = 1071 và b = 462.
Các hình vuông có kích thước 462×462 được đặt vào trong đó,
để lại một hình chữ nhật 462×147. Hình chữ nhật này được phủ bằng các
hình vuông 147×147 cho đến khi chỉ còn lại một hình chữ nhật 21×147,
rồi tiếp tục được phủ bằng các hình vuông 21×21, không còn diện tích không được phủ.
Kích thước hình vuông nhỏ nhất, 21, chính là USCLN của 1071 và 462.