Nhấn vào đây để đọc bằng ngôn ngữ khác: English

Cho một mảng các số nguyên không âm biểu diễn các sân thượng trong một bản đồ độ cao với chiều rộng của mỗi thanh là 1, tính toán xem sau cơn mưa có thể lấy được bao nhiêu nước.

Ví dụ #1

Input: arr[] = [2, 0, 2]
Output: 2
Cấu trúc như sau:

| |
|_|

Chúng ta có thể lấy được 2 đơn vị nước ở khoảng trống giữa.

Ví dụ #2

Input: arr[] = [3, 0, 0, 2, 0, 4]
Output: 10
Cấu trúc như sau:

     |
|    |
|  | |
|__|_|

Chúng ta có thể lấy được "3*2 đơn vị" nước giữa 3 và 2,
"1 đơn vị" trên đỉnh của thanh 2 và "3 đơn vị" giữa 2
và 4. Xem biểu đồ bên dưới để biết thêm.

Ví dụ #3

Input: arr[] = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]
Output: 6
Cấu trúc như sau:

       |
   |   || |
_|_||_||||||

Lấy "1 đơn vị" nước giữa số 1 đầu tiên và 2, "4 đơn vị" giữa
số 2 đầu tiên và 3 và "1 đơn vị" giữa số 1 cuối cùng và số 2 cuối cùng.

Một phần tử của mảng có thể chứa nước nếu có thanh cao hơn ở bên trái và bên phải. Chúng ta có thể tính được lượng nước có thể được lưu trữ trong mỗi phần tử bằng cách tìm chiều cao của thanh ở cả hai bên trái và phải. Ý tưởng là tính toán lượng nước có thể được lưu trữ trong mỗi phần tử của mảng. Ví dụ, xem xét mảng [3, 0, 0, 2, 0, 4], Chúng ta có thể lấy được "3*2 đơn vị" nước giữa 3 và 2, "1 đơn vị" trên đỉnh của thanh 2 và "3 đơn vị" giữa 2 và 4. Xem biểu đồ dưới đây để biết thêm.

Ý tưởng

Đối với mỗi phần tử trong mảng, chúng ta tìm mức nước cao nhất nó có thể lưu trữ sau cơn mưa, tức là bằng cách tính toán giá trị tối thiểu của chiều cao tối đa của thanh ở cả hai bên trái và phải trừ chiều cao của chính nó.

Bước thực hiện

• Khởi tạo answer = 0
• Lặp qua mảng từ trái sang phải:
  • Khởi tạo max_left = 0 và max_right = 0
  • Lặp từ phần tử hiện tại đến đầu mảng cập nhật: max_left = max(max_left, height[j])
  • Lặp từ phần tử hiện tại đến cuối mảng cập nhật: max_right = max(max_right, height[j])
  • Thêm min(max_left, max_right) − height[i] vào answer

Phân Tích Độ Phức Tạp

Độ phức tạp thời gian: O(n^2). Đối với mỗi phần tử của mảng, chúng ta lặp qua các phần bên trái và bên phải.

Độ phức tạp không gian phụ: O(1) không gian phụ.

Ý tưởng

Trong lực brute, chúng ta lặp lại phần bên trái và phải một lần nữa chỉ để tìm kích thước thanh cao nhất cho đến vị trí đó. Nhưng điều này có thể được lưu trữ. Đúng vậy, lập trình động.

Vì vậy, chúng ta có thể tính trước chiều cao cao nhất từ bên trái và phải của mỗi thanh trong O(n) thời gian. Sau đó sử dụng các giá trị được tính trước này để tìm lượng nước trong mỗi phần tử mảng.

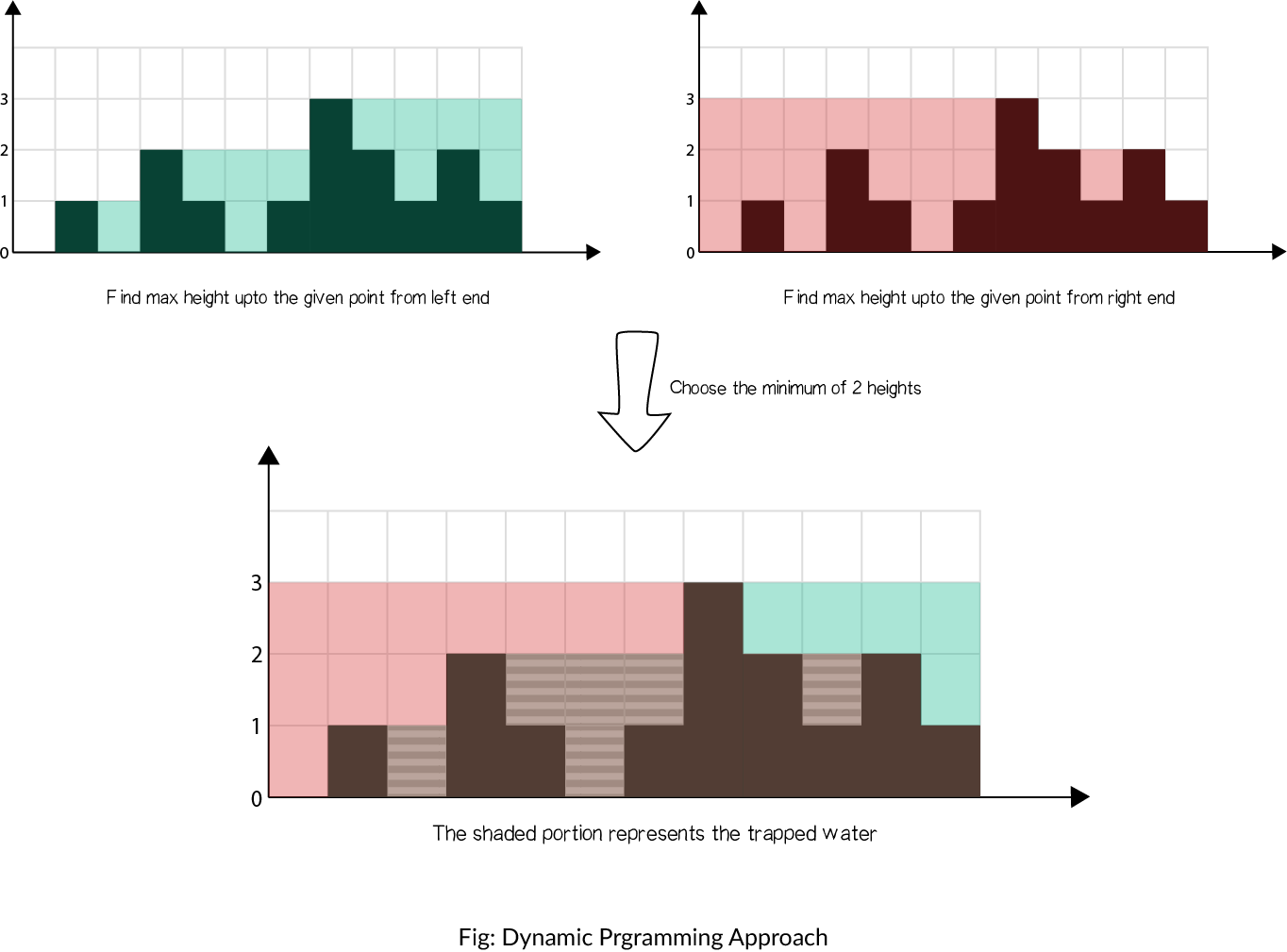
Khái niệm được minh họa như dưới đây:

Bước thực hiện

• Tìm chiều cao cao nhất của thanh từ đầu bên trái đến một chỉ số i trong mảng left_max.
• Tìm chiều cao cao nhất của thanh từ cuối bên phải đến một chỉ số i trong mảng right_max.
• Lặp qua mảng height và cập nhật answer:
  • Thêm min(max_left[i], max_right[i]) − height[i] vào answer.

Phân Tích Độ Phức Tạp

Độ phức tạp thời gian: O(n). Chúng ta lưu trữ các chiều cao tối đa cho đến một điểm bằng cách sử dụng 2 lặp O(n) mỗi lần. Cuối cùng, chúng ta cập nhật answer bằng cách sử dụng các giá trị đã lưu trữ trong O(n).

Độ phức tạp không gian phụ: O(n) không gian phụ. Dùng thêm không gian cho các mảng left_max và right_max so với Phương pháp 1.

• GeeksForGeeks
• LeetCode