Given a N*N board with the Knight placed on the first block of an empty board. Moving according to the rules of chess knight must visit each square exactly once. Print the order of each the cell in which they are visited.
Example:
Input :
N = 8
Output:
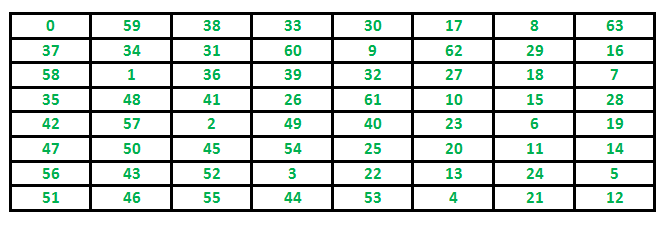
0 59 38 33 30 17 8 63
37 34 31 60 9 62 29 16
58 1 36 39 32 27 18 7
35 48 41 26 61 10 15 28
42 57 2 49 40 23 6 19
47 50 45 54 25 20 11 14
56 43 52 3 22 13 24 5
51 46 55 44 53 4 21 12
The path followed by Knight to cover all the cells Following is a chessboard with 8 x 8 cells. Numbers in cells indicate move number of Knight.
Following is the Backtracking algorithm for Knight’s tour problem.
If all squares are visited
print the solution
Else
a) Add one of the next moves to solution vector and recursively
check if this move leads to a solution. (A Knight can make maximum
eight moves. We choose one of the 8 moves in this step).
b) If the move chosen in the above step doesn't lead to a solution
then remove this move from the solution vector and try other
alternative moves.
c) If none of the alternatives work then return false (Returning false
will remove the previously added item in recursion and if false is
returned by the initial call of recursion then "no solution exists" )