蚁群算法学习视频 YouTube：【数之道 04】解决最优路径问题的妙招-蚁群ACO算法

什么是旅行商问题

  旅行商问题（英语：Travelling salesman problem, TSP）是组合优化中的一个NP困难问题，在运筹学和理论电脑科学中非常重要。问题内容为“给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。”

  问题在1930年首次被形式化，并且是在最优化中研究最深入的问题之一。许多优化方法都用它作为一个基准。尽管问题在计算上很困难，但已经有了大量的启发式和精确方法，因此可以完全求解城市数量上万的实例，并且甚至能在误差1%范围内估计上百万个城市的问题。

  甚至纯粹形式的TSP都有若干应用，如企划、物流、芯片制造。稍作修改，就是DNA测序等许多领域的一个子问题。在这些应用中，“城市”的概念用来表示客户、焊接点或DNA片段，而“距离”的概念表示旅行时间或成本或DNA片段之间的相似性度量。TSP还用在天文学中，观察很多光源的天文学家会希望减少在不同光源之间转动望远镜的时间。在许多应用场景中（如资源或时间窗口有限等等），可能会需要加入额外的约束条件。

  经典的TSP可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短。从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的Hamilton回路。由于该问题的可行解是所有顶点的全排列，随着顶点数的增加，会产生组合爆炸，它是一个NP完全问题。由于其在交通运输、电路板线路设计以及物流配送等领域内有着广泛的应用，国内外学者对其进行了大量的研究。

  早期的研究者使用精确算法求解该问题，常用的方法包括：分枝定界法、线性规划法、动态规划法等。但是，随着问题规模的增大，精确算法将变得无能为力，因此，在后来的研究中，国内外学者重点使用近似算法或启发式算法，主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等。

蚁群算法概述

  蚁群在外出觅食或者探索的时候，往往会留下弗洛蒙（信息素），每当该蚂蚁在此路径有良好的发现，就会将弗洛蒙浓度加大；反之，弗洛蒙浓度则会挥发，蚁群算法就是根据这一特点而被设计出来的。

首先我们对蚂蚁的功能进行定义：

1. 蚂蚁在一个旅程中不会访问相同的城市
2. 蚂蚁可以知晓城市之间的距离
3. 蚂蚁会在其走过的路上释放弗洛蒙（信息素）

之后建立函数 $P_{ij}^k$ 表示第k只蚂蚁从状态 $i$ 转移至状态 $j$ 的概率 公式如下： $P_{ij}^k=\frac{(\tau_{ij}^\alpha)(\eta_{ij}^\beta)}{\sum_{z\epsilon allowedx}(\tau_{ij}^\alpha)(\eta_{ij}^\beta)}$   其中$\tau_{ij}$为弗洛蒙浓度，$\eta_{ij}$为距离

• 其弗洛蒙浓度计算公式： $\tau_{ij}(t+1)=\rho*\tau_{ij}(t)+\triangle\tau_{ij}$ 其中$\rho$为佛罗蒙浓度挥发系数，$\triangle\tau_{ij}$为此次佛罗蒙浓度变化值 $\triangle\tau_{ij}={{Q}\over{L_k}}$ 其中Q为信息素增加强度系数，$L_k$为上期蚂蚁循环总路程 由上式可见，蚂蚁走过的路程越短与信息素浓度成反比；Q与信息素浓度成正比 又因为有$k$只蚂蚁，所以总$\triangle\tau_{ij}$为： $\triangle\tau_{ij}=\sum_{k=1}^m\triangle\tau_{ij}^k$

• 距离计算公式： $\eta_{ij}={1\over{d_{ij}}}$ 可见，距离越短，$\eta_{ij}$越大

• 公式中$\alpha$和$\beta$为权重控制系数 当$\alpha$为0时，完全根据城市距离做选择，一般都是局部最优，很难得到全局最优 当$\beta$为0时，完全根据佛罗蒙浓度做选择，程序迭代往往会以很快的速度收敛，很难达到预期效果

所以一般在使用蚁群算法时，我们要设定合适的$\alpha,\beta,\eta,\tau,Q$去获得很好的解

代码实现

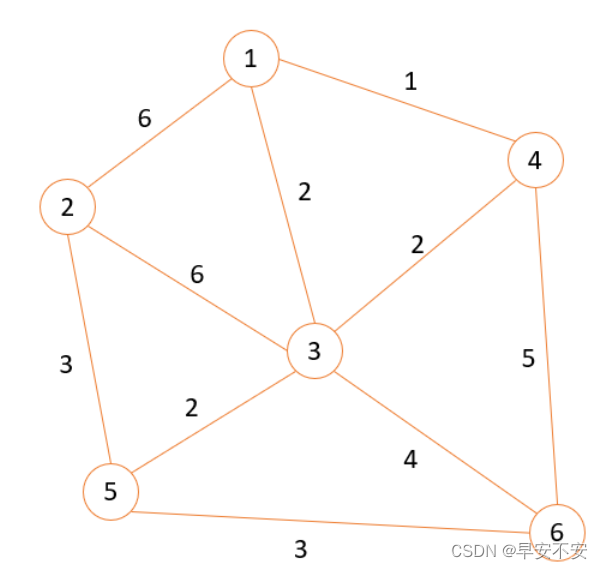
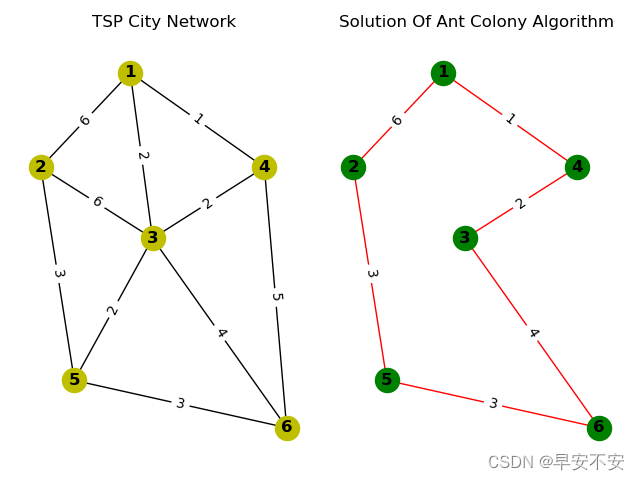
  此次实验以下图进行示例演示（哈哈，其实是因为课程要求是这个，偷个懒） 这里我对各别部分进行说明，其余地方注释详尽，自行查看即可   其中utils.py为可视化方法文件，主要打印程序运行时间、结果等文字，同时现实蚁群算法规划的路线图：   之后是ACO函数，即为蚁群算法的核心算法代码，调用时调用antColonyOptimization接口即可，接口相关解释如下：

def antColonyOptimization(cityNum, coordinate, point, setting):
    """
  蚁群算法
  :param cityNum: 城市数量 int
  :param coordinate: 城市坐标 list
  :param point: 城市距离矩阵 ndarray
  :param setting: 函数相关配置 obj
  :return: 最小距离 double, 运行时间 double, 迭代次数 int

  setting相关配置:
    iter_max: 最大迭代次数 int
    ifOptimanation: 是否使用简单优化后的方案 bool
    threshold: 阈值 int
    skipNum: 达到阈值后跳过的迭代次数 int
  示例:
    setting = {
      "iter_max": 500,
      "ifOptimanation": True,
      "threshold": 6,
      "skipNum": 20
    }
  """

最后为主函数demo.py，这里我就将旅行商地图赋值加入，其蚁群算法计算主要依赖point路径矩阵进行计算，coordinate为可视化中点的位置 demo.py:

import ACO
import numpy as np

# 旅行商测试矩阵
# 	1	2	3	4	5	6
# 1	0	6	2	1	MAX	MAX
# 2	6	0	6	MAX	3	MAX
# 3	2	6	0	2	2	4
# 4	1	MAX	2	0	MAX	5
# 5	MAX	3	2	MAX	0	3
# 6	MAX	MAX	4	5	3	0


# 旅行商初始化函数，总共6个城市
def InitD():
    cityNum = 6
    coordinate = [(4, 7.5), (0, 5.5), (5, 4), (10, 5.5), (1.5, 1), (11, 0)]
    MAX_INT = 1e8
    point = np.array([[0, 6, 2, 1, MAX_INT, MAX_INT], [6, 0, 6, MAX_INT, 3, MAX_INT], [2, 6, 0, 2, 2, 4],
                      [1, MAX_INT, 2, 0, MAX_INT, 5], [MAX_INT, 3, 2, MAX_INT, 0, 3], [MAX_INT, MAX_INT, 4, 5, 3, 0]])

    return cityNum, coordinate, point


def ACOTest():
    cityNum, coordinate, point = InitD()
    ACO.antColonyOptimization(cityNum, coordinate, point, setting={
        "iter_max": 300,
        "ifOptimanation": False,
        "threshold": 6,
        "skipNum": 20
    })


if __name__ == '__main__':
    ACOTest()