Skip to content

Latest commit

 

History

History
105 lines (64 loc) · 5.04 KB

README.md

File metadata and controls

105 lines (64 loc) · 5.04 KB
Raw

Table Of Content

Segmented-Sieve

Sieve of Eratosthenes is an algorithm for finding all the prime numbers in a segment [1:n] using O(n loglogn) operations.

Intro

Description

  • The basic idea of a segmented sieve is to choose the sieving primes less than the square root of n, choose a reasonably large segment size that nevertheless fits in memory, and then sieve each of the segments in turn, starting with the smallest.
  • At the first segment, the smallest multiple of each sieving prime that is within the segment is calculated, then multiples of the sieving prime are marked as composite in the normal way; when all the sieving primes have been used, the remaining unmarked numbers in the segment are prime. *Then, for the next segment, for each sieving prime you already know the first multiple in the current segment (it was the multiple that ended the sieving for that prime in the prior segment), so you sieve on each sieving prime, and so on until you are finished.

Implementations

The idea of a segmented sieve is to divide the range [0..n-1] in different segments and compute primes in all segments one by one. This algorithm first uses Simple Sieve to find primes smaller than or equal to √(n). Below are steps used in Segmented Sieve.

  • Use Simple Sieve to find all primes up to the square root of ‘n’ and store these primes in an array “prime[]”. Store the found primes in an array ‘prime[]’.
  • We need all primes in the range [0..n-1]. We divide this range into different segments such that the size of every segment is at-most √n
    • Do following for every segment [low..high]
    • Create an array mark[high-low+1]. Here we need only O(x) space where x is a number of elements in a given range. Iterate through all primes found in step 1. For every prime, mark its multiples in the given range [low..high].
  • In Simple Sieve, we needed O(n) space which may not be feasible for large n. Here we need O(√n) space and we process smaller ranges at a time (locality of reference)
Note

The time complexity (or a number of operations) by Segmented Sieve is the same as Simple Sieve.

Problem Statement

In this problem you have to print all primes from given interval. Input

t - the number of test cases, then t lines follows. [t <= 150] On each line are written two integers L and U separated by a blank. L - lower bound of interval, U - upper bound of interval. [2 <= L < U <= 2147483647] [U-L <= 1000000].

Output

For each test case output must contain all primes from interval [L; U] in increasing order.

Sample Input: 2 2 10 3 7

Sample Output: 2 3 5 7 3 5 7

Algorithm

An Efficient Approach is to solve the problem using offline queries and Fenwick Trees. Below are the steps:

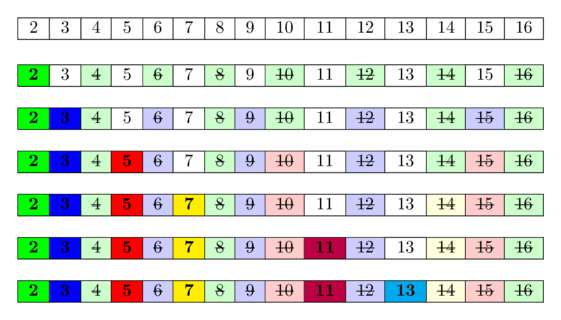
  • At the beginning we write down all numbers between 2 and n.

  • We mark all proper multiples of 2 (since 2 is the smallest prime number) as composite. A proper multiple of a number x, is a number greater than x and divisible by x.

  • Then we find the next number that hasn't been marked as composite, in this case it is 3. Which means 3 is prime, and we mark all proper multiples of 3 as composite. The next unmarked number is 5, which is the next prime number, and we mark all proper multiples of it. And we continue this procedure until we processed all numbers in the row.

  • In the following image you can see a visualization of the algorithm for computing all prime numbers in the range [1:16].It can be seen, that quite often we mark numbers as composite multiple times.

example

  • The idea behind is this: A number is prime, if none of the smaller prime numbers divides it. Since we iterate over the prime numbers in order, we already marked all numbers, who are divisible by at least one of the prime numbers, as divisible.

  • Hence if we reach a cell and it is not marked, then it isn't divisible by any smaller prime number and therefore has to be prime.

Time Complexity

  • The time complexity of calculating all primes below n in the random access machine model is O(n log log n) operations, a direct consequence of the fact that the prime harmonic series asymptotically approaches log log n.

  • It has an exponential time complexity with regard to input size, though, which makes it a pseudo-polynomial algorithm. The basic algorithm requires O(n) of memory.

  • The bit complexity of the algorithm is O(n (log n)(log log n)) bit operations with a memory requirement of O(n)

Advantages

  1. It has advantages for large ‘n’ as it has better locality of reference thus allowing better caching by the CPU and also requires less memory space.

Disadvantages

  1. It does slow down as the size increases.S