1444. Number of Ways of Cutting a Pizza

1444. Number of Ways of Cutting a Pizza (Hard)

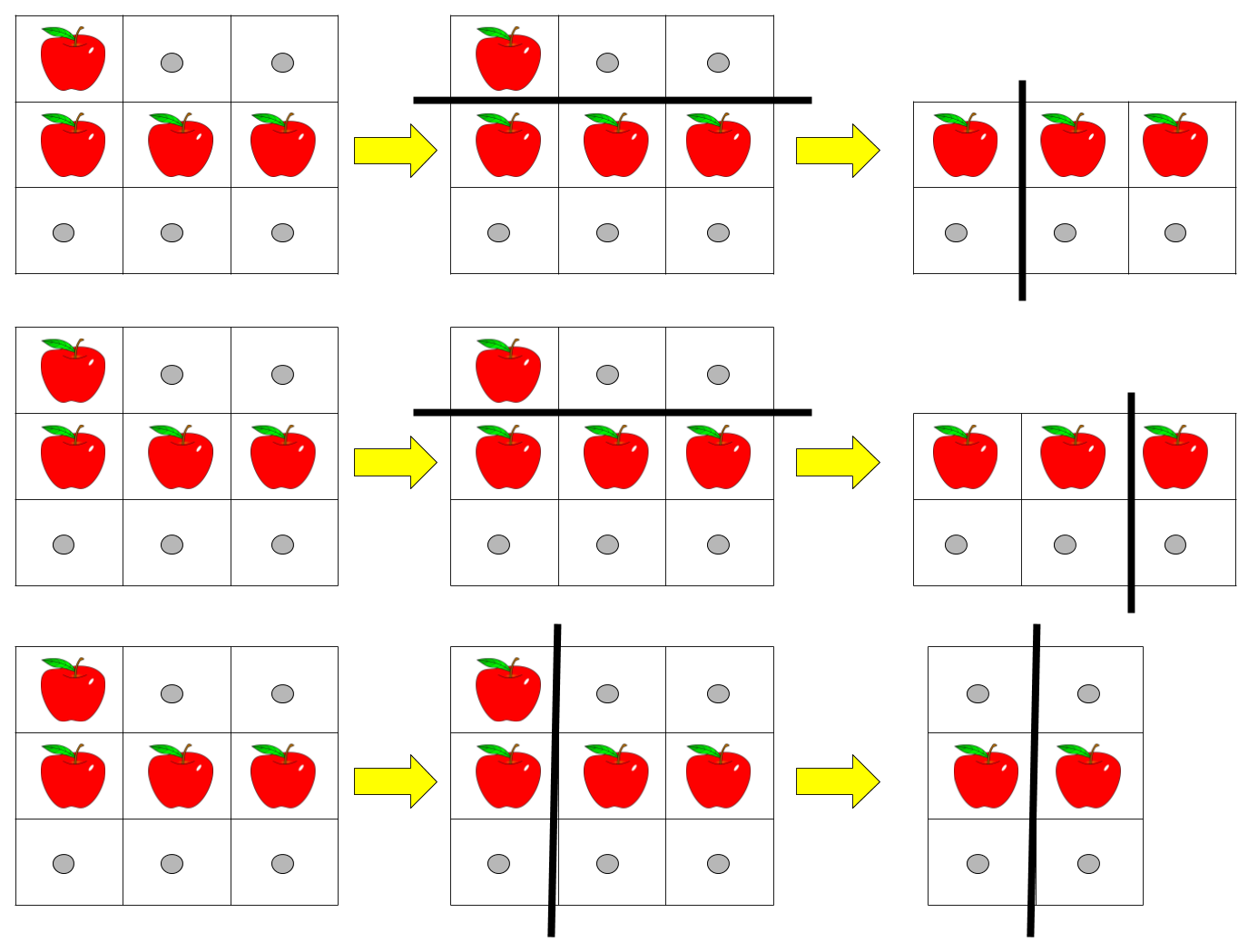
Given a rectangular pizza represented as a rows x cols matrix containing the following characters: 'A' (an apple) and '.' (empty cell) and given the integer k. You have to cut the pizza into k pieces using k-1 cuts. 

For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.

Return the number of ways of cutting the pizza such that each piece contains at least one apple. Since the answer can be a huge number, return this modulo 10^9 + 7.

 

Example 1:

Input: pizza = ["A..","AAA","..."], k = 3
Output: 3 
Explanation: The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.

Example 2:

Input: pizza = ["A..","AA.","..."], k = 3
Output: 1

Example 3:

Input: pizza = ["A..","A..","..."], k = 1
Output: 1

 

Constraints:

• 1 <= rows, cols <= 50
• rows == pizza.length
• cols == pizza[i].length
• 1 <= k <= 10
• pizza consists of characters 'A' and '.' only.

Related Topics:
Dynamic Programming

Solution 1. DP

Let dp[i][j][k] be the answer for the subproblem with k pieces and subarray from A[i][j] to A[M-1][N-1].

For each i, j, k, we should try:

1. Slice horizontally at row t where i < t < M. dp[i][j][k] += sum( dp[t][j][k - 1] | i < t < M && slicing at row t is valid )
2. Slice vertically at column t where j < t < N. dp[i][j][k] += sum( dp[i][t][k - 1] | j < t < N && slicing at column t is valid)

dp[i][j][k] = sum( dp[t][j][k - 1] | i < t < M && slicing at row t is valid )
              + sum( dp[i][t][k - 1] | j < t < N && slicing at column t is valid)
dp[i][j][1] = 1   // if there are any apples in the rectangle from `A[i][j]` to `A[M-1][N-1]`
              0   // otherwise

To check if slicing at row or column t is valid, we can precompute an array cnt where cnt[i][j] is the number of apples in the rectangle from A[i][j] to A[M-1][N-1].

If we slice at row t, then cnt[i][j] == cnt[t][j] means that there is no apples in rectangle A[i][j] to A[t][N-1], we should skip this t since it's an invalid slice.

cnt[t][j] == 0 means there is no apply in rectangle A[t][j] to A[M-1][N-1], we should break at t since further extending t won't results in any valid slice.

So we can update the formula as follows.

dp[i][j][k] = sum( dp[t][j][k - 1] | i < t < M && cnt[i][j] != cnt[t][j] && cnt[t][j] != 0 )
              + sum( dp[i][t][k - 1] | j < t < N && cnt[i][j] != cnt[i][t] && cnt[i]t] != 0 )
dp[i][j][1] = cnt[i][j] ? 1 : 0

// OJ: https://leetcode.com/problems/number-of-ways-of-cutting-a-pizza/
// Author: github.com/lzl124631x
// Time: O(MNK * max(M, N))
// Space: O(MNK)
class Solution {
    void add(long &a, long &b) { a = (a + b) % ((int) 1e9+7); }
public:
    int ways(vector<string>& A, int K) {
        int M = A.size(), N = A[0].size();
        vector<vector<int>> cnt(M + 1, vector<int>(N + 1));
        for (int i = M - 1; i >= 0; --i) {
            int s = 0;
            for (int j = N - 1; j >= 0; --j) {
                s += A[i][j] == 'A';
                cnt[i][j] = cnt[i + 1][j] + s;
            }
        }
        vector<vector<vector<long>>> dp(M + 1, vector<vector<long>>(N + 1, vector<long>(K + 1)));
        for (int i = M - 1; i >= 0; --i) {
            for (int j = N - 1; j >= 0; --j) {
                dp[i][j][1] = cnt[i][j] > 0;
                for (int k = 2; k <= K; ++k) {
                    for (int t = i + 1; t < M; ++t) {
                        if (cnt[i][j] == cnt[t][j]) continue;
                        if (cnt[t][j] == 0) break;
                        add(dp[i][j][k], dp[t][j][k - 1]);
                    }
                    for (int t = j + 1; t < N; ++t) {
                        if (cnt[i][j] == cnt[i][t]) continue;
                        if (cnt[i][t] == 0) break;
                        add(dp[i][j][k], dp[i][t][k - 1]);
                    }
                }
            }
        }
        return dp[0][0][K];
    }
};