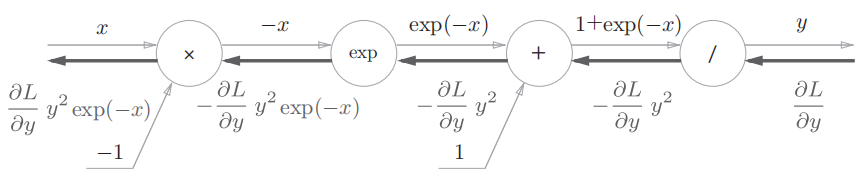人类大脑是一个可以产生意识、思想和情感的器官。它是人体最复杂的器官,由神经元、神经胶质细胞、神经干细胞和血管组成。其中,神经元(Neuron),也叫神经细胞(Nerve Cell),是携带和传输信息的细胞,是人脑神经系统中最基本的单元。人脑神经系统是一个非常复杂的组织,包含近860亿个神经元,每个神经元有上千个突触和其他神经元相连接。这些神经元和它们之间的连接形成巨大的复杂网络。
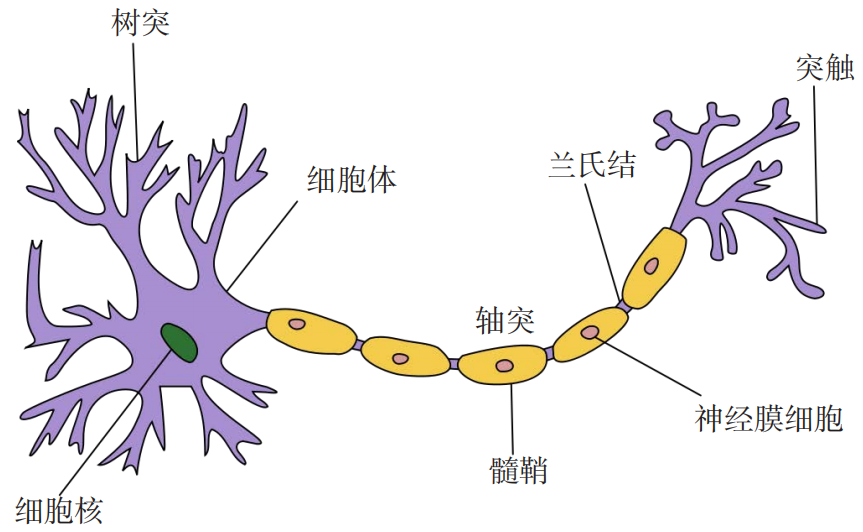
典型的神经元结构大致可分为细胞体和细胞突起。
(1) 细胞体(Soma)中的神经细胞膜上有各种受体和离子通道,胞膜的受体可与相应的化学物质神经递质结合,引起离子通透性及膜内外电位差发生改变,产生相应的生理活动:兴奋或抑制。
(2) 细胞突起是由细胞体延伸出来的细长部分,又可分为树突和轴突。
-
树突(Dendrite)可以接收刺激并将兴奋传入细胞体,每个神经元可以有一或多个树突;
-
轴突(Axon)可以把自身的兴奋状态从胞体传送到另一个神经元或其他组织,每个神经元只有一个轴突;
神经元可以接收其他神经元的信息,也可以发送信息给其他神经元。神经元之间没有物理连接,两个“连接”的神经元之间留有 20 纳米左右的缝隙,并靠突触进行互联来传递信息,形成一个神经网络,即神经系统。
突触可以理解为神经元之间的连接“接口”,将一个神经元的兴奋状态传到另一个神经元。一个神经元可被视为一种只有两种状态的细胞:兴奋和抑制。神经元的状态取决于从其他的神经细胞收到的输入信号量,以及突触的强度(抑制或加强)。当信号量总和超过了某个阈值时,细胞体就会兴奋,产生电脉冲。电脉冲沿着轴突并通过突触传递到其他神经元。
人工神经网络是为模拟人脑神经网络而设计的一种计算模型,它从结构、实现机理和功能上模拟人脑神经网络.人工神经网络与生物神经元类似,由多个节点(人工神经元)互相连接而成,可以用来对数据之间的复杂关系进行建模。
不同节点之间的连接被赋予了不同的权重,每个权重代表了一个节点对另一个节点的影响大小。每个节点代表一种特定函数,来自其他节点的信息经过其相应的权重综合计算,输入到一个激活函数中并得到一个新的活性值(兴奋或抑制)。从系统观点看,人工神经元网络是由大量神经元通过极其丰富和完善的连接而构成的自适应非线性动态系统。
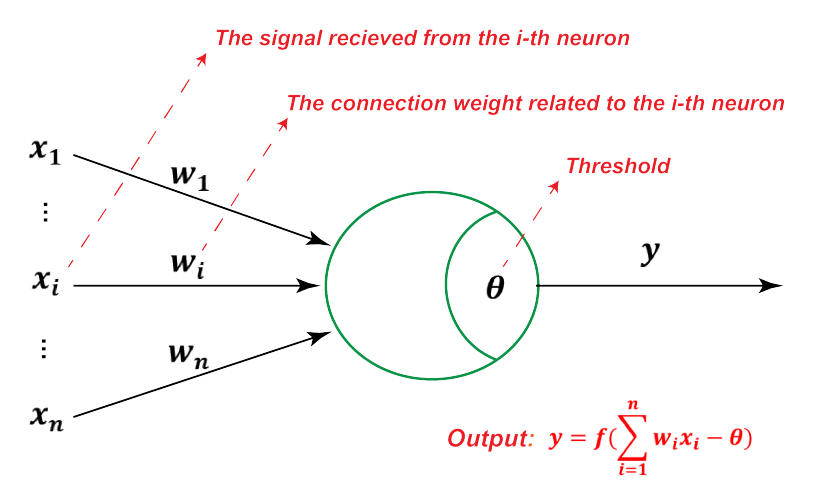
1943 年,心理学家 McCulloch 和数学家 Pitts 根据生物神经元的结构,提出了一种非常简单的神经元模型,MP神经元。现代神经网络中的神经元和 MP 神经元的结构并无太多变化。不同的是,MP 神经元中的激活函数
假设一个神经元接收到了
其中,$\boldsymbol{w}=[w_1;w_2;...;w_n]\in \mathbb{R}^N$ 为
神经元的激活与否取决于某一阈值电平,只有当其输入的总和超过
这种“阈值加权和”的神经元模型称为 M-P模型 ( McCulloch-Pitts Model ),也称为神经网络的一个 处理单元( PE, Processing Element )。
激活函数
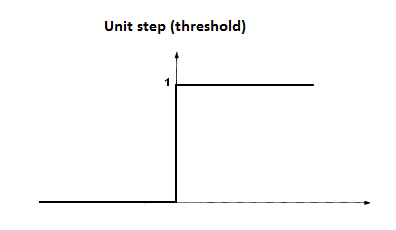
理想中的激活函数为阶跃函数,它可以将输入值映射为
为了增强网络的表示能力和学习能力,激活函数需要具备以下几点性质:
(1) 连续并可导(允许少数点上不可导)的非线性函数.可导的激活函数可以直接利用数值优化的方法来学习网络参数。
(2) 激活函数及其导函数要尽可能的简单,有利于提高网络计算效率。
(3) 激活函数的导函数的值域要在一个合适的区间内,不能太大也不能太小,否则会影响训练的效率和稳定性。
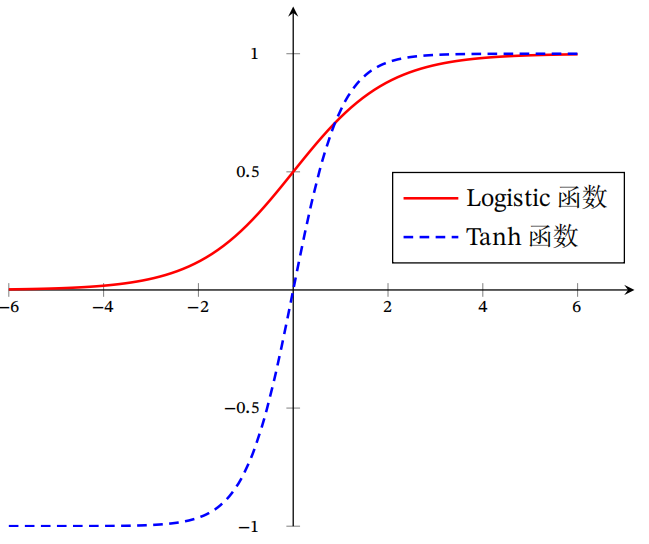
常用的 Sigmoid 函数有 Logistic 函数和 Tanh 函数,它们的形状都呈 S 型,均为两端饱和函数。所谓两端饱和,指的是当变量
-
Logistic 函数定义: $$ \sigma(x)=\frac{1}{1+\exp (-x)} $$
- Logistic 函数将输入压缩到
$0-1$ 之间,输入越大越接近$1$ ,输入越小越接近$0$ 。这与生物神经元类似,对一些输入进行了激活(输出$1$ ) ,对另一些输入进行了抑制(输出$0$ )。同时这也为模型引入非线性,可以提高模型的表达能力。 - 由于 Logistic 函数在两端的导数趋近
$0$ ,随着神经网络的加深,也会带来梯度消失的问题(后面会解释)。
- Logistic 函数将输入压缩到
-
Tanh 函数定义: $$ \tanh (x)=\frac{\exp (x)-\exp (-x)}{\exp (x)+\exp (-x)} $$
- 前面的 Logistic 函数的输出是非零中心化的,输出都在同一侧(恒大于
$0$ ),这回带来偏置偏移的问题,进一步使得梯度收敛速度变慢。而Tanh 函数是零中心化的,一定程度上缓解了收敛速度变慢的问题。 - 但是由于 Tanh 函数是两端饱和的函数,仍然会引发梯度消失的问题。
- 前面的 Logistic 函数的输出是非零中心化的,输出都在同一侧(恒大于
ReLU(Rectified Linear Unit,修正线性单元),是目前使用最广泛的激活函数。定义为: $$ \begin{aligned} \operatorname{ReLU}(x) &=\left{\begin{array}{ll} x & \text { if } \ x \geq 0 \ 0 & \text { if } \ x<0 \end{array}\right.\ \ &=\max (0, x) \end{aligned} $$ 优点:
-
采用 ReLU 的神经元只需要进行加、乘和比较操作,计算上更加高效。
-
具有生物学合理性,单侧抑制,宽兴奋边界。在生物神经网络中,同时处于兴奋状态的神经元也非常稀疏,同一时刻大约
$1%-4%$ 。而 ReLU 具有很好地稀疏性,同时只有$50%$ 的神经元处于兴奋状态。 -
在优化方面,ReLU 函数为左饱和函数,且只有当
$x>0$ 时梯度为$1$ ,在一定程度上缓解了梯度消失的问题,有利于加速梯度下降收敛。
缺点:
-
ReLU 函数的输出是非零中心化的,相当于后一层神经网络引入了偏置偏移,会影响梯度下降效率。
-
ReLU 神经元在训练时容易死亡,如果参数在一次不恰当的更新后,第一个隐藏层中的某个 ReLU 神经元在所有的训练数据上都不能被激活,那么这个神经元自身参数的梯度永远都会是
$0$ , 在以后的训练过程中永远不能被激活。
Leaky ReLU $$ \begin{aligned} \text { LeakyReLU }(x) &=\left{\begin{array}{ll} x & \text { if } x>0 \ \gamma x & \text { if } x \leq 0 \end{array}\right. \ \ &=\max (0, x)+\gamma \min (0, x), \end{aligned} $$
Leaky ReLU 针对 ReLU 神经元死亡的问题,在输入
高斯线性激活单元(Gaussian Error Linear Unit, GELU):
该激活函数在 Bert 中经常被使用,详细资料可见文末参考文献。
要想模拟人脑的能力,单一的神经元是远远不够的,需要通过很多神经元一起协作来完成复杂的功能。这样通过一定的连接方式或信息传递方式进行协作的神经元可以看作一个网络,就是神经网络。
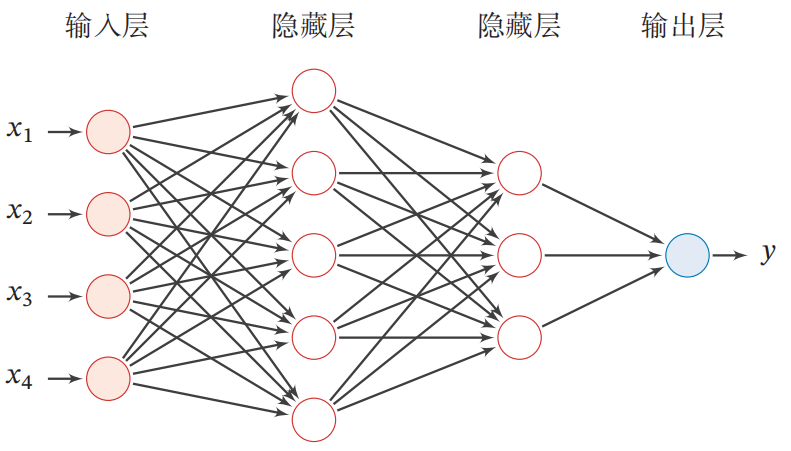
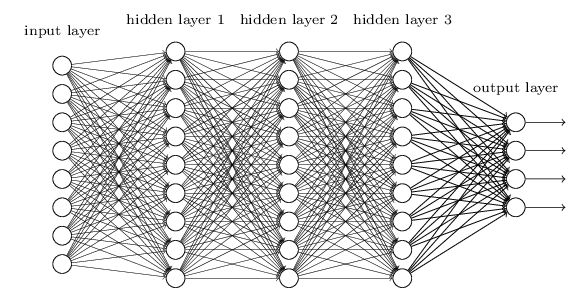
前馈神经网络(Feedforward Neural Network,FNN)是最早发明的简单人工神经网络。前馈神经网络也经常称为多层感知器(Multi-Layer Perceptron,MLP),但其实二者还是有一定区别,多层感知机的激活函数为阶跃函数,前馈神经网路的激活函数为连续非线性函数。在前馈神经网络中,各神经元分别属于不同的层.每一层的神经元可以接收前一层神经元的信号,并产生信号输出到下一层。第0层称为输入层,最后一层称为输出层,其他中间层称为隐藏层。令第一层的输入为
$$
\begin{aligned}
\boldsymbol{z}^{(l)} &=\boldsymbol{W}^{(l)} \boldsymbol{a}^{(l-1)}+\boldsymbol{b}^{(l)} \ \
\boldsymbol{a}^{(l)} &=f_{l}\left(\boldsymbol{z}^{(l)}\right)
\end{aligned}
$$
其中,
这样,前馈神经网络可以通过逐层进行信息传递,得到网络最后的输出
对于多层的前馈神经网络,在训练时需要更强大的学习算法。反向传播算法(error BackPropagation,简称BP)算法就是其中最杰出的代表,现实任务中,大多数是使用 BP 算法进行训练,其不仅可用于前馈神经网络,还可用于其它的神经网络,如递归神经网络。
通常我们在说 BP 网络时,指的是使用 BP 算法训练的多层前馈神经网络。本小节将详细介绍反向传播算法的原理以及过程。
假设存在
反正传播的计算顺序是,将信号
- 这里说的局部导数指的是正向传播中
$y=f(x)$ 的导数,就是$y$ 关于$x$ 的导数$\frac{\partial y}{\partial x}$ 。 - 然后将这个局部导数乘以上游传递过来的值(
$E$ ), 再传递给下游的节点。
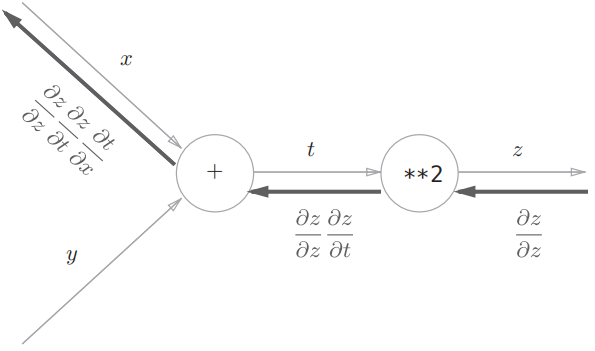
在介绍链式法则之前,我们先来回顾一下复合函数:复合函数是由多个函数构成的函数。例如,$z=(x+y)^2$ 由两个式子构成: $$ z = t^2 \ t = x +y $$ 链式法则是关于复合函数的导数的性质,定义如下:
- 如果某个函数由复合函数表示,则该复合函数的导数可以用构成复合函数的各个函数的乘积表示。
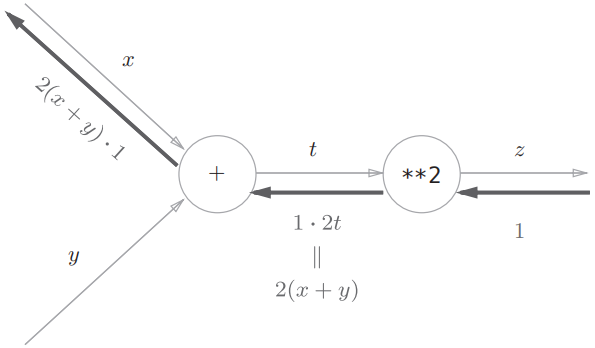
以上面的函数举例,即: $$ \frac{\partial z}{\partial x}=\frac{\partial z}{\partial t} \frac{\partial t}{\partial x}=2t \cdot 1=2(x+y) $$ 将链式法则用计算图表示,如下:
反向传播步骤
前面已经说明了神经网络的反向传播时基于链式法则的,我们在计算每一层不同参数的梯度时,只需按照两个步骤即可:
- 计算当前层,输出
$f(x)$ 关于输入$x$ 的梯度$f'$ 。 - 将当前层的梯度
$f'$ 乘以上游传播回来的梯度$E$ ,即可得到目标函数$L(x,...)$ 关于$x$ 的梯度。 - 最后,将当前输入的梯度继续往下游进行传播。
梯度计算总结
这里总结了不同函数下的导数计算,假设上游传递过来的梯度记为
- 若当前层为简单的
$+, -$ 运算时:就按照上游传播的值原封不动传播下去即可。 - 若当前层为输入
$x$ 和输出$y$ 关系:$y=wx+b$ ,那么$x$ 的梯度为 $ E \times w$。- 同理可以计算参数
$w$ 的梯度为 $ E\times x$; - 同理可以计算参数
$b$ 的梯度为 $ E $;
- 同理可以计算参数
- 若当前层为输入
$x$ 和输出关系$y$ :$y = log x$ , 那么$x$ 的梯度为 $E \times \frac{1}{x} $ ; - 若当前层为输入
$x$ 和输出关系$y$ :$y = \frac{1}{x}$ , 那么$x$ 的梯度为 $E \times -\frac{1}{x^2} $ ; - 若当前层为输入
$x$ 和输出关系$y$ :$y = e^x$ , 那么$x$ 的梯度为$E \times e^x$ ;
举例
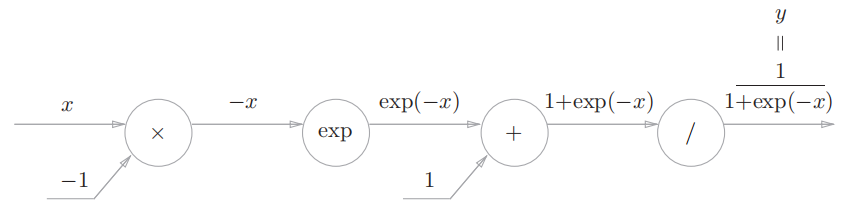
这里以 Logistic 函数的反向传播为例,函数公式如下: $$ y=\frac{1}{1+exp(-x)} $$ 用计算图可以表示为:
可以看到,复杂的公式经过拆解,已经没那么复杂了。现在,按照前面总结的反向传播规则,可以得到加上反向传播后的计算图:
-
以最后一个运算
$/$ (除法)为例,令输入$t=1+exp(-x)$ ,则输出$y=\frac{1}{t}$ ,有: $$ \begin{aligned} \frac{\partial y}{\partial t} &=-\frac{1}{t^{2}} \ \ &=-y^{2} \end{aligned} $$ -
梯度
$\frac{\partial L}{\partial y} y^{2} \exp (-x)$ 可以进一步整理为: $$ \begin{aligned} \frac{\partial L}{\partial y} y^{2} \exp (-x) &=\frac{\partial L}{\partial y} \frac{1}{(1+\exp (-x))^{2}} \exp (-x) \ &=\frac{\partial L}{\partial y} \frac{1}{1+\exp (-x)} \frac{\exp (-x)}{1+\exp (-x)} \ &=\frac{\partial L}{\partial y} y(1-y) \end{aligned} $$
SoftMax 函数以及交叉熵损失函数在反向传播过程中梯度的计算会更复杂,但是也可以按照链式法将其进行分解后来计算。具体可以参考书籍**《深度学习的入门:基于Python的理论和实现》**中附录 A (P267~P277)。
对于一些层数较深的神经网络模型,在训练时可能会出现一些问题,其中就包括梯度消失问题(gradient vanishing problem)和梯度爆炸问题(gradient exploding problem)。梯度消失问题和梯度爆炸问题一般随着网络层数的增加会变得越来越明显。
我们知道前馈神经网络的传播公式如下:
$$
\begin{aligned}
\boldsymbol{z}^{(l)} &=\boldsymbol{W}^{(l)} \boldsymbol{a}^{(l-1)}+\boldsymbol{b}^{(l)}
\ \
\boldsymbol{a}^{(l)} &=f_{l}\left(\boldsymbol{z}^{(l)}\right)
\end{aligned}
$$
例如,现在有一个层数为
\begin{array}{l}
\frac{\partial \boldsymbol{L}}{\partial \boldsymbol{W}^{(0)}}
\ =
\frac{\partial \boldsymbol{L}}{\partial \boldsymbol{a}^{(n)}}
\times
(\frac{\partial \boldsymbol{a}^{(n)}}{\partial \boldsymbol{z}^{(n)}}
\frac{\partial \boldsymbol{z}^{(n)}}{\partial \boldsymbol{a}^{(n-1)}})
\times
(\frac{\partial \boldsymbol{a}^{(n-1)}}{\partial \boldsymbol{z}^{(n-1)}}\frac{\partial \boldsymbol{z}^{(n-1)}}{\partial \boldsymbol{a}^{(n-2)}})
\times
\dots
\times
(\frac{\partial \boldsymbol{a}^{(1)}}{\partial \boldsymbol{z}^{(1)}}\frac{\partial \boldsymbol{z}^{(1)}}{\partial \boldsymbol{W}^{(0)}})
\=
\frac{\partial \boldsymbol{L}}{\partial \boldsymbol{a}^{(n)}}
\times (f^{\prime}\left(\boldsymbol{z}^{(n)}) \cdot \boldsymbol{W}^{(n)} \right)
\times (f^{\prime}\left(\boldsymbol{z}^{(n-1)}) \cdot \boldsymbol{W}^{(n-1)} \right)
\times
\dots
\times (f^{\prime}\left(\boldsymbol{z}^{(1)}) \cdot \boldsymbol{a}^{(0)} \right)
\end{array} $$ 梯度消失
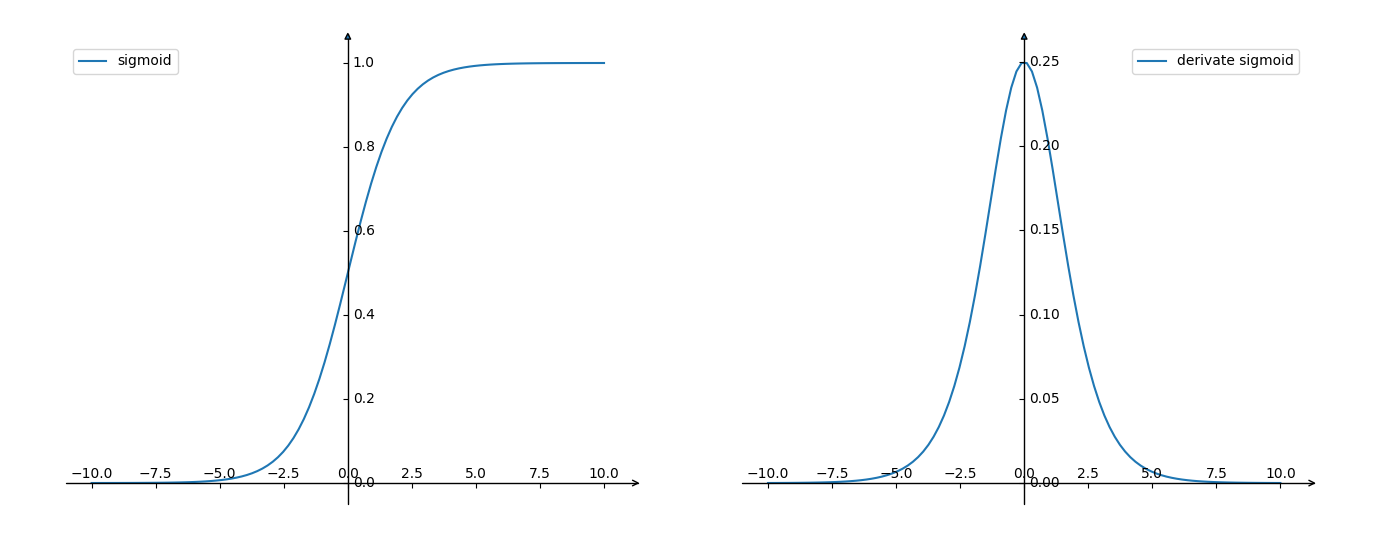
根据Sigmoid 函数的表达式,其函数图像(左)及其导数图像(右)如下:
可以看出,Sigmoid 函数的导数取值范围在
梯度爆炸
对于 Sigmoid 激活函数的神经网络,梯度爆炸很难发生。如果发生了,可能的原因是权重$ \boldsymbol{W}$的初始化不合理。当
梯度爆炸和梯度消失问题都是因为网络太深,网络权值更新不稳定造成的,本质上是因为梯度反向传播中的连乘效应,这不是说使用更小的学习率就能改善的。对于更普遍的梯度消失问题,可以考虑用ReLU激活函数取代Sigmoid激活函数。
在介绍神经网络在推荐系统中的应用之前,说明一点:在后面或者其它论文中出现的DNN(Deep Neural Networks)网络,或者多层感知机MLP,实际上指代的都是前面提到的前馈神经网络。在实际应用中,可能不同层之间的激活函数有所改变。
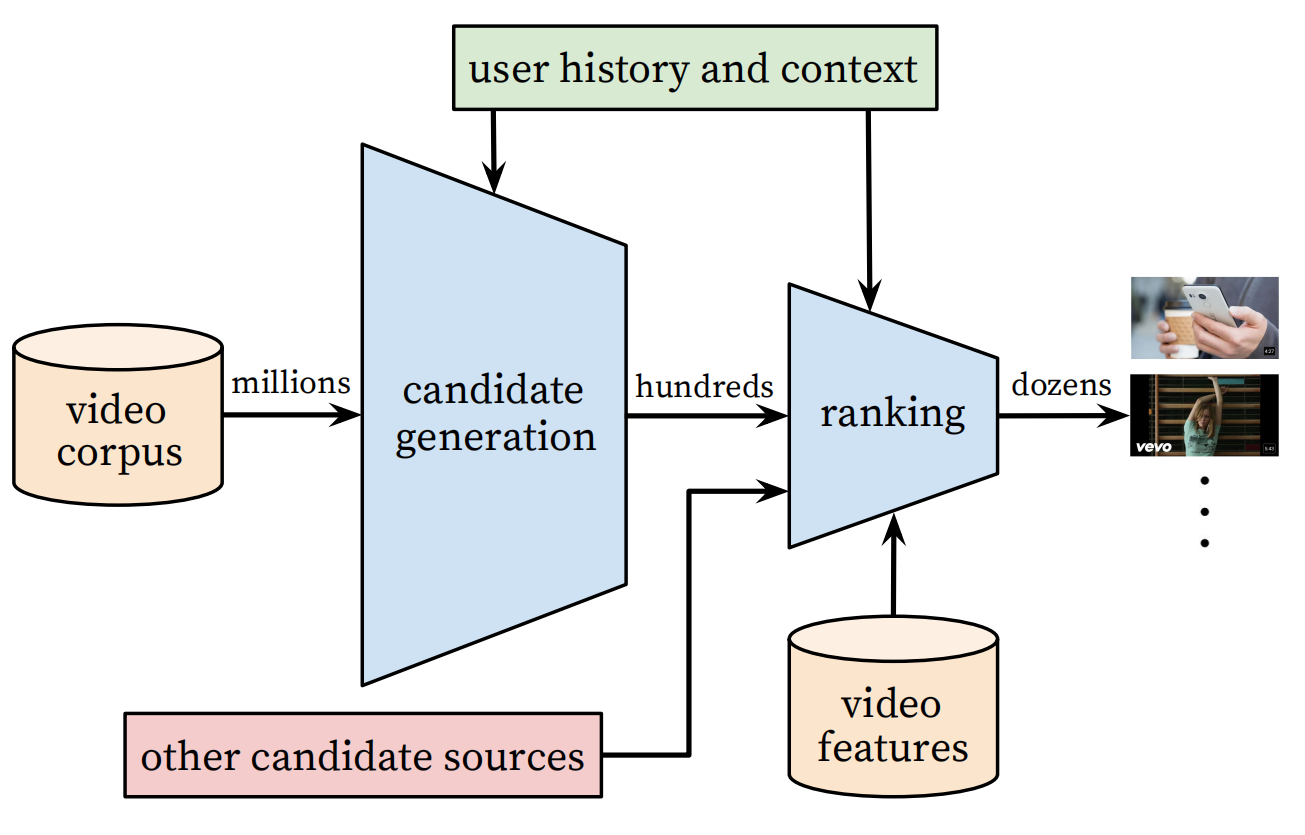
Youtube 作为全球最大的 UGC 的视频网站,需要在百万量级的视频规模下进行个性化推荐。由于候选视频集合过大,考虑 online 系统延迟问题,不宜用复杂网络直接进行推荐,所以 YoutubeDNN 采取了两个阶段来完成整个推荐过程:
从上图可以看出,YoutubeDNN 包含了两个阶段分别为:
- Candidate Generation:候选物品产生阶段,也就是我们常说的召回阶段,也可以称为检索(retrieval)阶段。该阶段的目的旨在完成候选视频的快速筛选,这一步候选视频集合由百万降低到了百的量级。由于需要处理的候选物品数量较多,所以该阶段的模型不能太复杂,且使用的特征信息较排序阶段更少。
- Ranking:排序阶段,这一阶段主要是完成对几百个候选视频的精排。由于候选物品数量不像召回阶段那么多,所以可以使用更复杂的排序模型,以及更丰富的用户、物品等特征信息。
本文后面会简单介绍召回阶段和排序阶段,关于 YoutubeDNN 模型的详细阶段可以看原论文或者本小节末给出的相关链接,由于 YoutubeDNN 模型包含了大量工程上的经验,建议学习的初期阶段了解流程即可(后续可深入)。
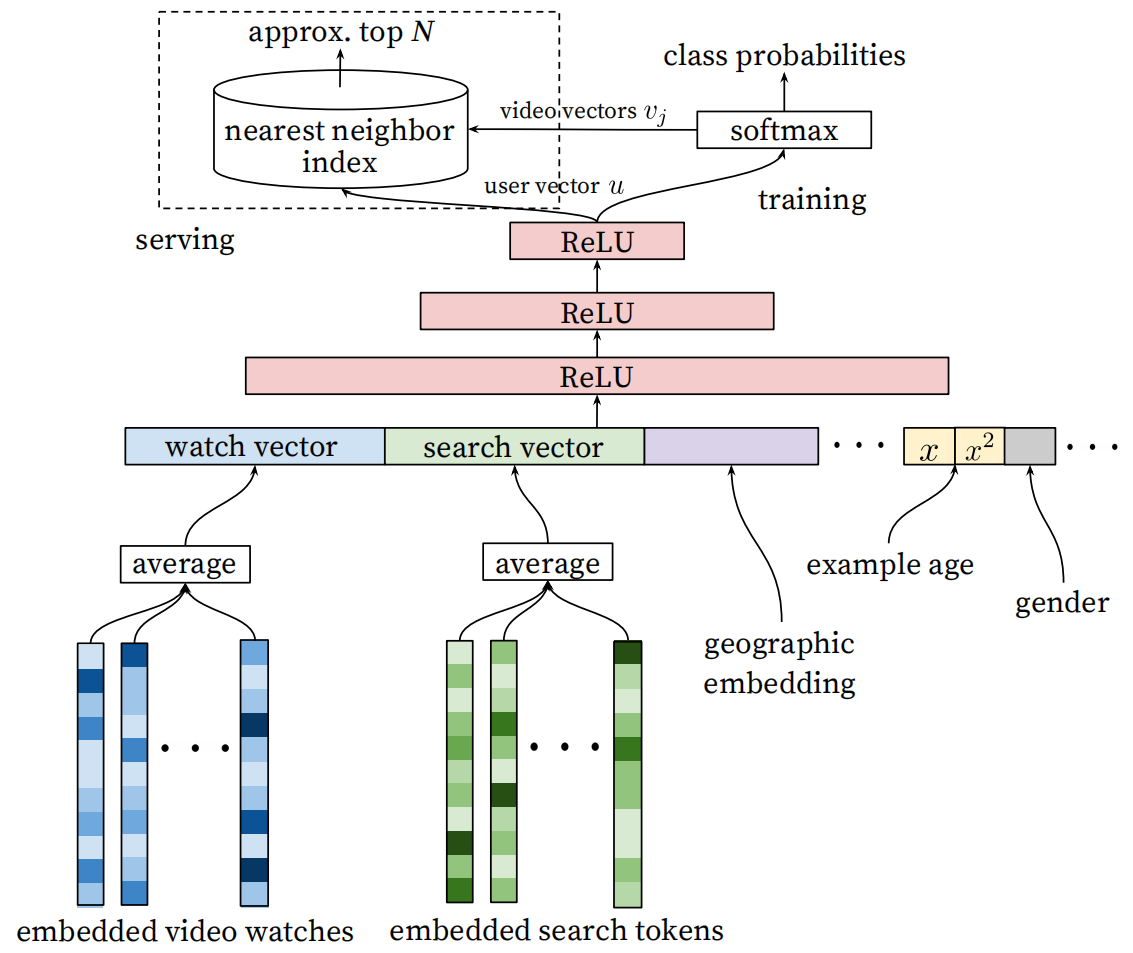
召回阶段的模型结构如下图:
从模型的结构来看,召回阶段使用的模型并不复杂,为包含多层神经网络的 DNN 模型。下面简单分析模型的流程:
-
特征输入
- embedded video watches:该输入为用户历史观看过的视频,每个视频的 Embedding 向量是通过词向量模型学习到的(word2vec),最后将所有观看过的视频的 Embedding 向量平均后作为输入。
- embedded search tokens:该输入为用户历史搜索记录,它的处理方式与观看历史类似:每个查询都被标记为 unigrams 和 bigrams,然后将标记进行向量 Embedded,最后将Embedding 向量平均后输入模型。
- geographic embedding:地理人口特征是很重要的,特别是对于新用户。主要用到的包括了 geographic region 以及 device,这对新缓解冷启动问题有帮助。
- 其它特征:example age,gender等等,这些特征在原文中有着不同的特征工程处理,引入后也有着不同的作用,这里不详细展开。
-
模型学习
- 从图上可以看出,论文将特征输入到一个激活函数为 ReLU 的多层前馈神经网络,学习到了用户的向量
$u$ 。
- 从图上可以看出,论文将特征输入到一个激活函数为 ReLU 的多层前馈神经网络,学习到了用户的向量
-
物品召回
-
召回采用的是一种最近邻检索算法,就是根据数据的相似性,从数据库中寻找与目标数据最相似的项目。这种相似性通常会被量化到空间上数据之间的距离,可以认为数据在空间中的距离越近,则数据之间的相似性越高。
-
如果采用最近邻检索,那么每个视频也应该对于一个向量。根据原文的表述,召回阶段最后的目标函数为 softmax 函数: $$ P\left(w_{t}=i \mid U, C\right)=\frac{e^{v_{i} u}}{\sum_{j \in V} e^{v_{j} u}} $$
- 所以,这里物品向量就是通过这个softmax 函数学习到的。我们知道 softmax 函数输出的值在
$(0,1)$ 之间,所以这里其实就是预测用户观看视频的概率。 - 原文对 softmax 函数做了一些改进。可以注意分母,如果计算所有视频向量与用户向量的指数内积,那么计算量是巨大的,原论文为了提高效率,使用了负采样的方法。
- 最后还有一点需要注意,输入时历史观看视频的向量与召回阶段的视频向量不是同一个概念,它们是通过不同方式学习的。
- 所以,这里物品向量就是通过这个softmax 函数学习到的。我们知道 softmax 函数输出的值在
-
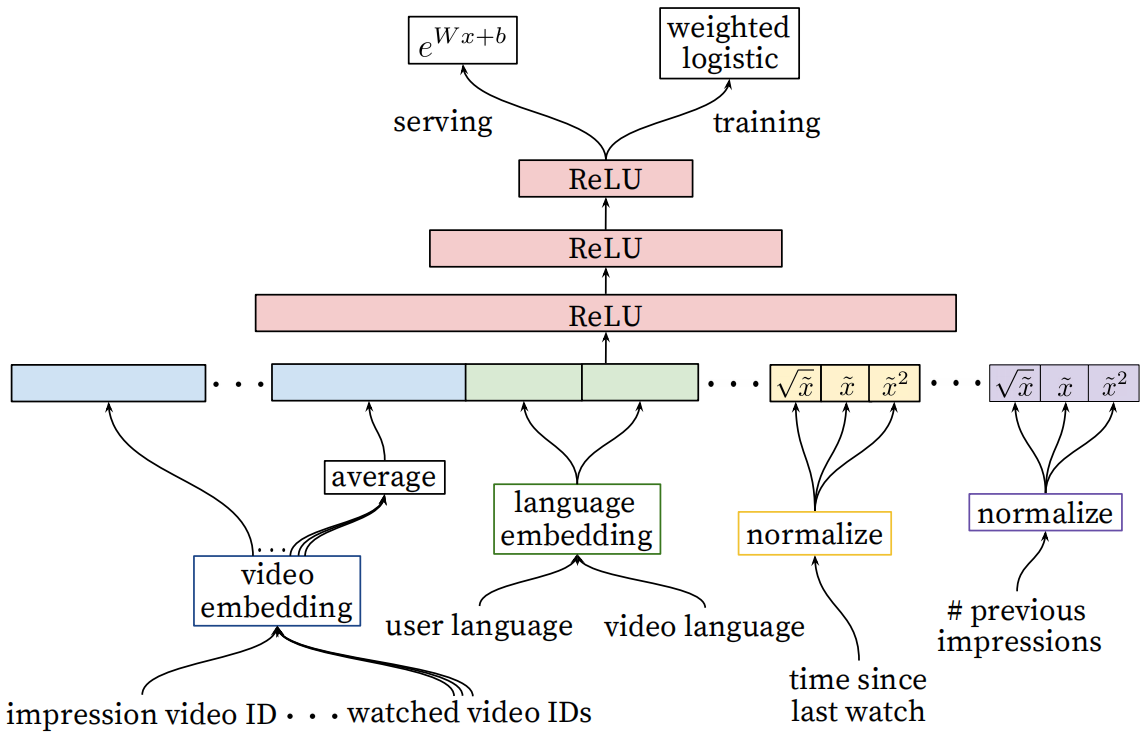
排序阶段的模型结构如下图:
可以看出,该阶段使用的模型与前面召回阶段相同,均为 DNN 模型。不同的是:
- 特征输入:
- 该阶段的输入的特征相较于召回阶段更丰富,这里就不再详细展开了,可以看上图了解输入了那些特征。
- 具体的特征工程和动机还是需要阅读原论文或部分博客了解。
- 目标预测:
- 召回阶段在训练时通过 softmax 函数,预测的是用户观看视频的概率。
- 排序阶段通过加权逻辑回归(weighted logistic),预测的是用户观看 impression video ID 的观看时长。
总结
本文只是简单介绍了 YoutubeDNN 的大致流程,算法具体的原理可参考如下的链接:
《Deep Neural Networks for YouTube Recommendations》:https://dl.acm.org/doi/pdf/10.1145/2959100.2959190
重读Youtube深度学习推荐系统论文-王喆:https://zhuanlan.zhihu.com/p/52169807
YouTube深度学习推荐系统的十大工程问题-王喆:https://zhuanlan.zhihu.com/p/52504407
揭开YouTube深度推荐系统模型Serving之谜-王喆:https://zhuanlan.zhihu.com/p/61827629
EMBEDDING 在大厂推荐场景中的工程化实践:https://lumingdong.cn/engineering-practice-of-embedding-in-recommendation-scenario.html#YouTube
Wide&Deep是谷歌发表在 DLRS 2016 上的文章《Wide & Deep Learning for Recommender System》。它的核心思想是结合线性模型的记忆能力和 DNN 模型的泛化能力,从而提升整体模型性能。
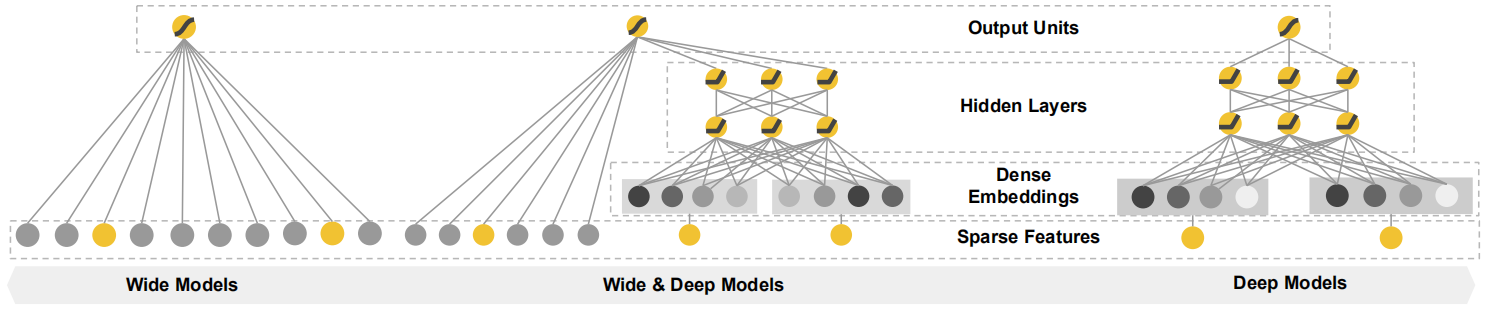
Wide & Deep 已成功应用到了 Google Play 的 app 推荐业务,具体的模型结构如下:
从结构图上看,Wide&Deep 由两部分组成,分别为 Wide 部分和 Deep 部分。简单来说,Wide 部分就是一个线性层,Deep 部分为多层前馈神经网络层,下面先对原理进行介绍:
Wide部分:
wide 部分就是一个广义线性模型(上图左),它的表达式为:
$$
y=\mathbf{w}^{T} \mathbf{x}+b
$$
-
$c_{k i}$ 为布尔变量,取值为${0,1}$ 。当原始特征$\mathbf{x}$ 中第$i$ 个特征属于第$k$ 个变换时,$c_{k i}=1$, 否则$c_{k i}=0$ 。 -
举个例子吧,假如原始特征为
$\mathbf{x}=[0.3, 0.2, 0.6, 0.5]$ ,现在只有第$1$ 个特征($0.3$)和第$3$ 个特征 ($0.6$)属于第$k$ 个变换的一部分,那么计算过程为: $$ \phi_{k}(\mathbf{x})=0.3^1 \cdot 0.2^0 \cdot 0.6^1 \cdot 0.5^0 = 0.18 $$ -
若存在
$n$ 个变换,那么会就生成$n$ 个新的特征。
最后将原始特征和交叉积变换后生成的特征拼接后,送入线性层即可。
Deep部分:
deep 部分就是前馈神经网络层,利用神经网络表达能力强的特点,进行深层的特征交叉,挖掘藏在特征背后的数据模式。 $$ a^{(l+1)}=f\left(W^{(l)} a^{(l)}+b^{(l)}\right) $$ Wide & Deep
最终,利用逻辑回归模型,输出层将 Wide 部分和 Deep 部分的输出组合起来,送入到逻辑回归模型
由于逻辑回归模型输出的值在
前面我们了解了整个模型的原理和过程,现在我们来理解谷歌为什么这么建模,这样做有什么好处。
- 首先说一下 Deep 部分,通过多层前馈网络,可以对特征向量的各个维度进行交叉组合,使得模型可以抓取到更丰富的非线性特征和组合特征信息。该部分极大地增强了模型的表达能力,同时使得模型的"泛化能力"(generalization)得到了很大提升(**“泛化能力”**可以被理解为模型传递特征的相关性,以及发掘稀疏甚至从未出现过的稀有特征与最终标签相关性的能力)。
- 虽然 Deep 层具有很大的优势,但随着网络层的加深,对于原始输入中的强特征记忆却变得没有简单模型那么深刻。所以,Deep &Cross模型在左侧还引入了简单的线性层,目的就是为了加深模型对强特征的记忆能力。线性层还通过交叉积变换引入了人工组合的特征,使得模型对这类强特的印象更深刻。这里引入《深度学习推荐系统》中的一段解释:
- 假设在 Google Play 推荐模型的训练过程中,设置如下组合特征:AND (user_installed_app=netflix,impression_app=pandora)(简称 netflix&pandora),它代表用户已经安装了netflix这款应用,而且曾在应用商店中看到过pandora这款应用。
- 如果以“最终是否安装pandora”为数据标签(label),则可以轻而易举地统计出netflix&pandora这个特征和安装pandora这个标签之间的共现频率。假设二者的共现频率高达10%(全局的平均应用安装率为1%),这个特征如此之强,以至于在设计模型时,希望模型一发现有这个特征,就推荐pandora这款应用(就像一个深刻的记忆点一样印在脑海里),这就是所谓的模型的“记忆能力”。
- 像逻辑回归这类简单模型,如果发现这样的“强特征”,则其相应的权重就会在模型训练过程中被调整得非常大,这样就实现了对这个特征的直接记忆。
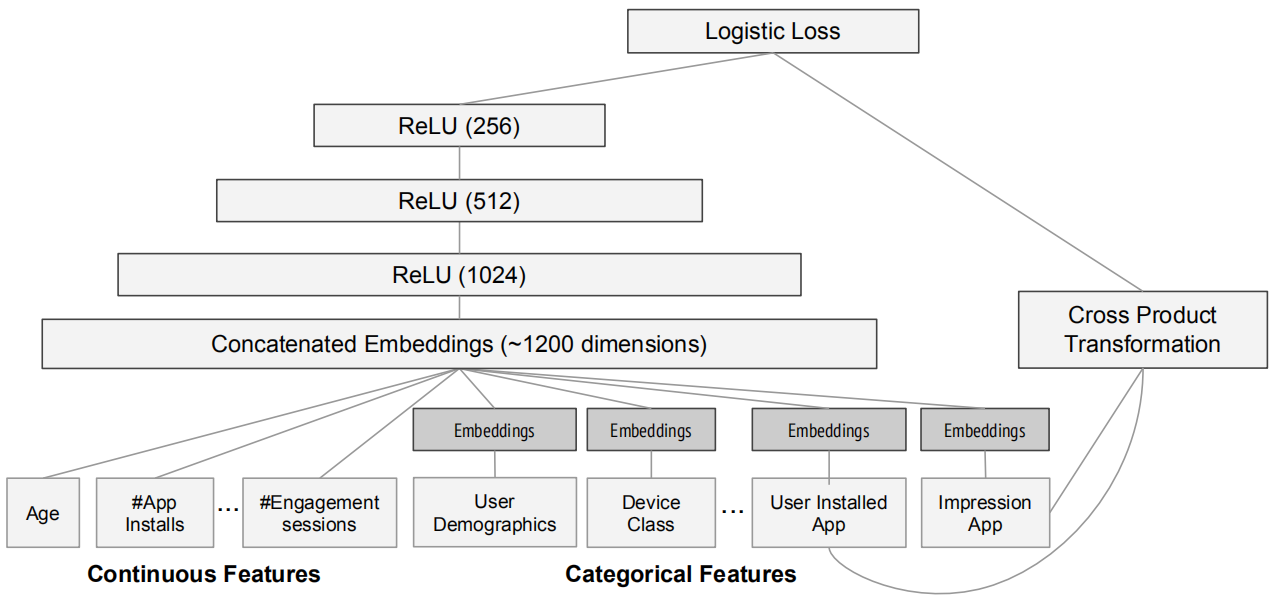
下图,是谷歌在应用商店中的推荐模型架构:
-
Deep 部分的输入是全量的特征向量,包括用户年龄(Age)、已安装应用数量(#App Installs)、设备类型(Device Class)、已安装应用(User Installed App)、曝光应用( Impression App)等特征。已安装应用、曝光应用等类别型特征,需要经过Embedding层输入连接层(Concatenated Embedding),拼接成1200维的Embedding向量,再依次经过3层ReLU全连接层,最终输入LogLoss输出层。
-
Wide 部分的输入仅仅是已安装应用和曝光应用两类特征,其中已安装应用代表用户 的历史行为,而曝光应用代表当前的待推荐应用。选择这两类特征的原因是充分发挥Wide部分“记忆能力”强的优势。
- 《神经网络和深度学习》,邱锡鹏著
- 《深度学习的入门:基于Python的理论和实现》,斋藤康毅【日】著
- 《机器学习》,周志华著
- 《深度学习推荐系统》,王喆著
- BERT中的激活函数GELU:https://zhuanlan.zhihu.com/p/349492378
- 神经网络训练中的梯度消失与梯度爆炸:https://zhuanlan.zhihu.com/p/25631496
- 《Wide & Deep Learning for Recommender Systems》:https://dl.acm.org/doi/pdf/10.1145/2988450.2988454
- 《Deep Neural Networks for YouTube Recommendations》:https://dl.acm.org/doi/pdf/10.1145/2959100.2959190
- 重读Youtube深度学习推荐系统论文-王喆:https://zhuanlan.zhihu.com/p/52169807
- YouTube深度学习推荐系统的十大工程问题-王喆:https://zhuanlan.zhihu.com/p/52504407
- 揭开YouTube深度推荐系统模型Serving之谜-王喆:https://zhuanlan.zhihu.com/p/61827629
- EMBEDDING 在大厂推荐场景中的工程化实践:https://lumingdong.cn/engineering-practice-of-embedding-in-recommendation-scenario.html#YouTube