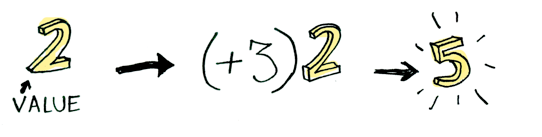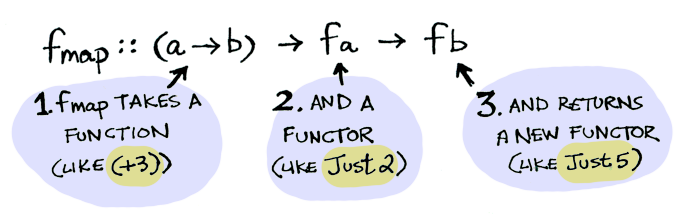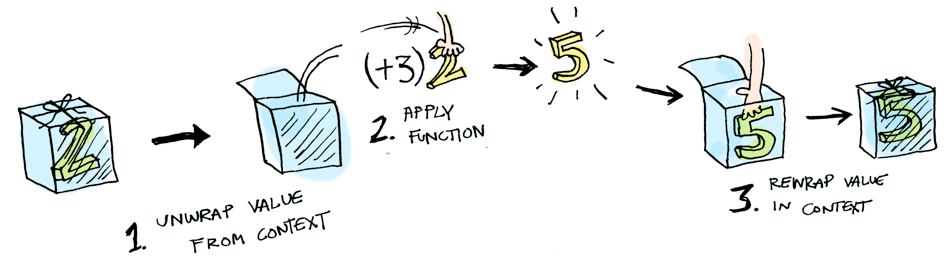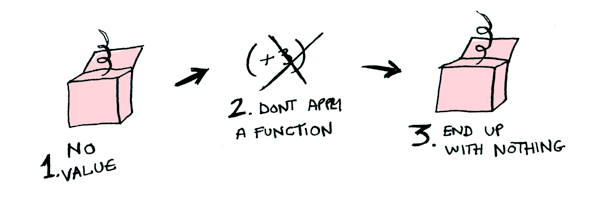Functors, Applicatives, And Monads In Pictures

This is a translation of Functors, Applicatives, And Monads In Pictures. This time we tried to translate it from English to some other language, but from Haskell into Python. Hopefully this should make the article much easier to understand for people who don't know Haskell.

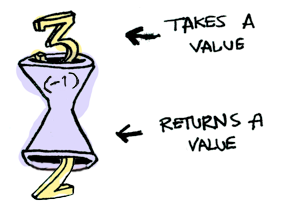
Here’s a simple value:

And we know how to apply a function to this value:

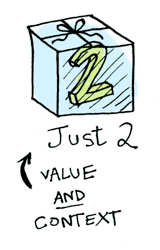
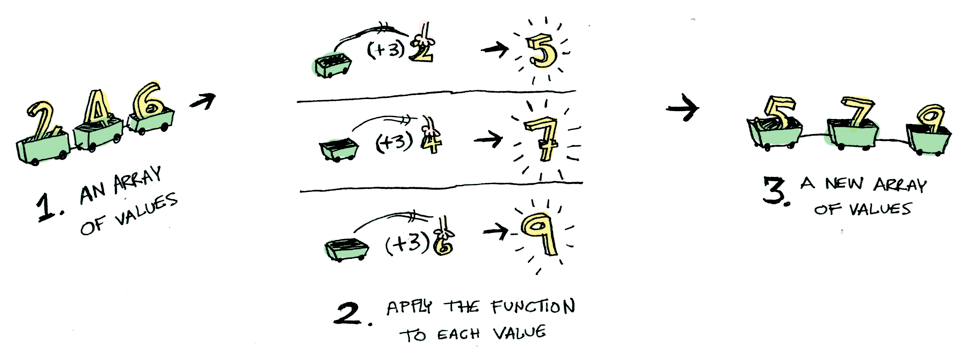
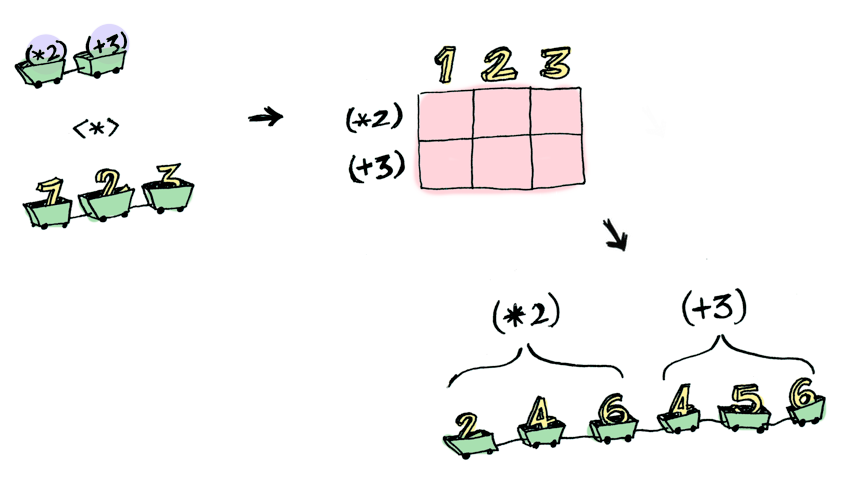
Simple enough. Lets extend this by saying that any value can be in a context. For now you can think of a context as a box that you can put a value in:

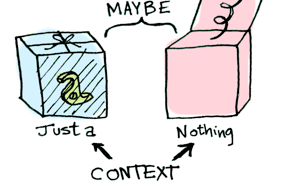
Now when you apply a function to this value, you’ll get different results depending on the context. This is the idea that Functors, Applicatives, Monads, Arrows etc are all based on. The Maybe data type defines two related contexts:

class Maybe(Monad, Monoid, Applicative, Functor, metaclass=ABCMeta):
    """The Maybe type encapsulates an optional value. A value of type Maybe a
    either contains a value of (represented as Just a), or it is empty
    (represented as Nothing). Using Maybe is a good way to deal with errors or
    exceptional cases without resorting to drastic measures such as error.
    """
    ...

In a second we’ll see how function application is different when something is a Just a versus a Nothing. First let’s talk about Functors!

Functors

When a value is wrapped in a context, you can’t apply a normal function to it:

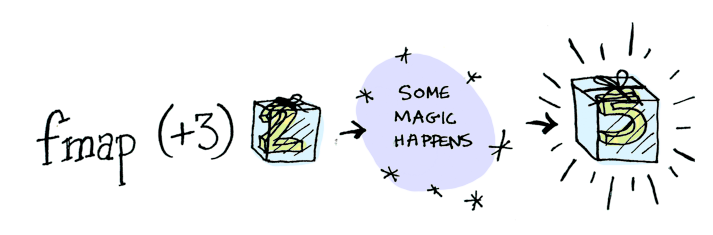
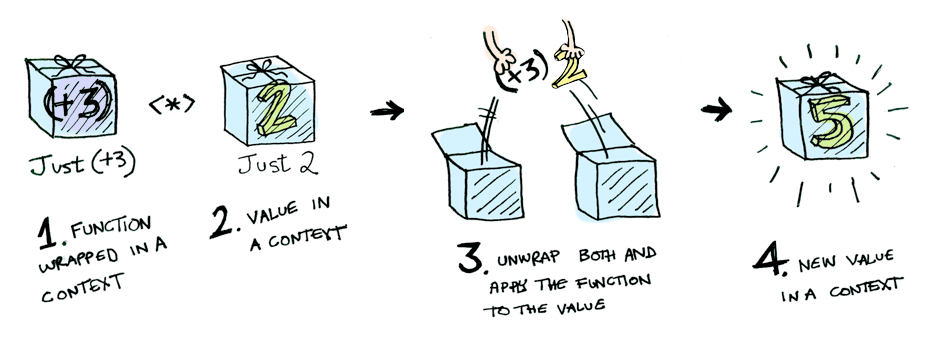
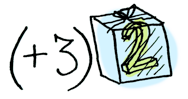
This is where fmap comes in. fmap is from the street, fmap is hip to contexts. fmap knows how to apply functions to values that are wrapped in a context. For example, suppose you want to apply (+3) to Just 2. Use fmap:

> Just(2).fmap(lambda x: x+3)
Just 5

Bam! fmap shows us how it’s done! But how does fmap know how to apply the function?

Just what is a Functor, really?

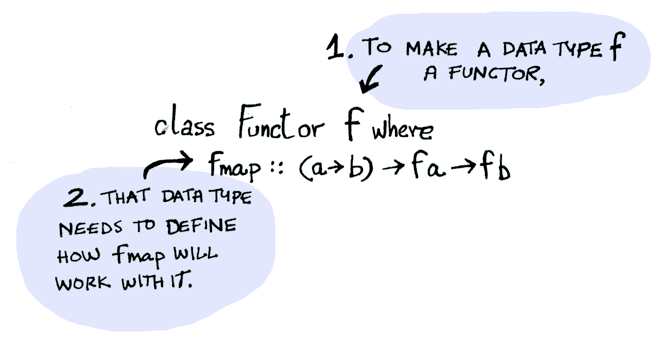
Functor is a typeclass. Here’s the definition:

A Functor is any data type that defines how fmap applies to it. Here’s how fmap works:

So we can do this:

> Just(2).fmap(lambda x: x+3)
Just 5

And fmap magically applies this function, because Maybe is a Functor. It specifies how fmap applies to Justs and Nothings:

class Just(Maybe):
    def fmap(self, mapper) -> Maybe:
        value = self._get_value()
        try:
            result = mapper(value)
        except TypeError:
            result = partial(mapper, value)

        return Just(result)

class Nothing(Maybe):
    def fmap(self, _) -> Maybe:
        return Nothing()

Here’s what is happening behind the scenes when we write Just(2).fmap(lambda x: x+3):

So then you’re like, alright fmap, please apply lambda x: x+3 to a Nothing?

> Nothing().fmap(lambda x: x+3)
Nothing

Bill O’Reilly being totally ignorant about the Maybe functor

Like Morpheus in the Matrix, fmap knows just what to do; you start with Nothing, and you end up with Nothing! fmap is zen. Now it makes sense why the Maybe data type exists. For example, here’s how you work with a database record in a language without Maybe:

post = Post.find_by_id(1)
if post
  return post.title
else
  return nil
end

But in Python:

find_post(1).fmap(get_post_title)

If find_post() returns a post, we will get the title with get_post_title. If it returns Nothing, we will return Nothing! Pretty neat, huh? <$> is the infix version of fmap, so you will often see this instead:

get_post_title & find_post(1)

Here’s another example: what happens when you apply a function to a list?

Lists are functors too! Here’s the definition:

class List(Monad, Monoid, Applicative, Functor, list)

Okay, okay, one last example: what happens when you apply a function to another function?

fmap(lambda x: x:+2, lambda y: y+3)

Here’s a function applied to another function:

The result is just another function!

>>> def fmap(f, g):
...   return lambda x: g(f(x))
...
>>> foo = fmap(lambda x: x+3, lambda y: y+2)
>>> foo(10)
15

So functions are Functors too!

Note: Functions are not really Functors in Python, but you could see that it was actually quite easy to define an fmap function in Python that made it possible for us to compose functions.

When you use fmap on a function, you’re just doing function composition!

Applicatives

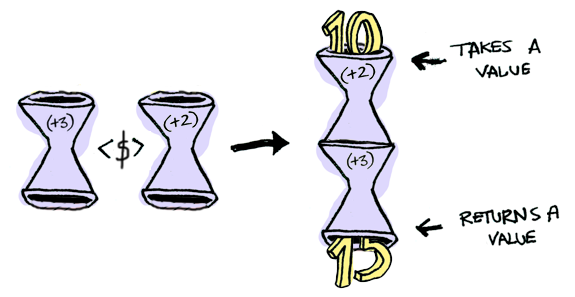
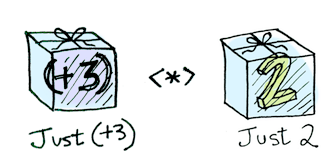
Applicatives take it to the next level. With an applicative, our values are wrapped in a context, just like Functors:

But our functions are wrapped in a context too!

Yeah. Let that sink in. Applicatives don’t kid around. Control.Applicative defines <*>, which knows how to apply a function wrapped in a context to a value wrapped in a context:

i.e:

>>> Just(lambda x: x+3) * Just(2) == Just(5)
True

Using * can lead to some interesting situations. For example:

>> List([lambda x: x*2, lambda y: y+3]) * List([1, 2, 3])
[2, 4, 6, 4, 5, 6]

Here’s something you can do with Applicatives that you can’t do with Functors. How do you apply a function that takes two arguments to two wrapped values?

>>> (lambda x,y: x+y) % Just(5)
Just functools.partial(<function <lambda> at 0x1003c1bf8>, 5)

>>> Just(lambda x: x+5) % Just(5)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: unsupported operand type(s) for <<: 'Just' and 'Just'

Applicatives:

>>> (lambda x,y: x+y) % Just(5)
Just functools.partial(<function <lambda> at 0x1003c1bf8>, 5)

>>> Just(lambda x: x+5) * Just(5)
Just 10

Applicative pushes Functor aside. “Big boys can use functions with any number of arguments,” it says. “Armed with % and *, I can take any function that expects any number of unwrapped values. Then I pass it all wrapped values, and I get a wrapped value out! AHAHAHAHAH!”

>>> (lambda x,y: x*y) % Just(5) * Just(3)
Just 15

And hey! There’s a function called liftA2 that does the same thing:

>>> Just(5).lift_a2(lambda x,y: x*y, Just(3))
Just 15

Monads

How to learn about Monads:

1. Get a PhD in computer science.
2. Throw it away because you don’t need it for this section!

Monads add a new twist.

Functors apply a function to a wrapped value:

Applicatives apply a wrapped function to a wrapped value:

Monads apply a function that returns a wrapped value to a wrapped value. Monads have a function >> (>>= in Haskell) (pronounced “bind”) to do this.

Let’s see an example. Good ol’ Maybe is a monad:

Just a monad hanging out

Suppose half is a function that only works on even numbers: