当提及常见算法时,深度优先搜索(DFS)和广度优先搜索(BFS)必然名列其中。许多学习者一旦掌握了DFS和BFS,就似乎对算法了如指掌,确实如此。掌握了这两个算法,就能利用计算机强大的计算能力迅速求解大多数问题,好多算法虽然搜索不是最优解,但也为一种极佳选择。
回溯算法,作为五大经典算法之一,实际上也是DFS的一种应用。当我们回忆八皇后问题时,就能体会到回溯算法的精髓。尽管DFS和BFS的基础学习思想相对简单,编写模板代码也不是难事,但在此基础上进行灵活变通却常常颇具挑战。
初步学习DFS和BFS的原理相对简单,但要精通它们却颇具难度。许多问题在这两者的基础上进行变形和优化,例如在DFS中可能涉及各种剪枝问题,而BFS可能需要考虑许多贪心策略,还可能涉及到记忆化、双向BFS、BFS+DFS等复杂技巧。然而,本文主要介绍基础概念,更深层次的探讨需要通过刷题实践来学习。
DFS和BFS通常用于解决图的行相关问题,因此在深入问题之前,首先需要关注图的存储方式。一般情况下,我们使用邻接矩阵或邻接表来存储图(这里不讨论十字链表、压缩矩阵等空间优化方法)。
邻接矩阵: 邻接矩阵是用数组(二维)表示图的一种方式。通常,我们对图中的各个节点进行顺序编号,矩阵中的数值表示图中节点的连接情况或路径长度。
- 无权图:通常使用布尔数组的 0 和 1 表示连接性。
- 有权图:数组的值表示两节点之间的路径长度,0 表示不通。
- 无向图:矩阵对称;有向图:通常非对称。
下面是一个具体例子。虽然这种方式操作更清晰、更便于实现,但容易导致空间浪费,因此有些人进行了空间优化,或选择使用邻接表存储图。
邻接表:
观察上面的领接矩阵,如果节点很多但是联通路径很少,那么就浪费了太多的存储空间,这种情况就更适合邻接表。
邻接表一般是数组套链表,比起邻接矩阵节省不少空间(直接存储联通信息或者路径),在存储的时候可以根据数据格式要求灵活运用容器(无权图省事一些,有权图可能需要自定义一个Node类型)。
但是正常的无向图依然会重复浪费一半空间,就有十字链表,多重链接表等等出现优化(大佬们的优化是真的牛批),但在算法逻辑上稍复杂,不过一般图论算法更注重的是算法的优化这里就不介绍十字链表了(虽然我也忘了),一个邻接表存储的图可以看下图:
概念:
深度优先搜索(DFS)是一种图算法,英文缩写为DFS,即Depth First Search。其核心思想是通过递归深入每个可能的分支路径直至无法深入,每个节点只能访问一次。
如果在迷宫中dfs那么dfs部分路径如下:
简单来说,DFS就是在图中按照一定规则进行搜索,通常通过递归实现。DFS就像一种黑魔法,设计好算法后它自动进行搜索。在使用DFS时,需要关注算法初始化、搜索规则、以及结束条件。一个最简单的DFS就是二叉树的前序遍历,也是很多人第一次接触到的DFS。
我们通常使用邻接表或邻接矩阵来存储图的信息,这里的例子使用邻接矩阵。
DFS的基本流程可以概括为:
- 从某个节点开始,按照一个方向一直遍历到尽头,同时标记已经访问过的节点。
- 遍历到尽头后,回退到上一个节点,同时清除当前节点的标记。然后在下一个方向遍历一次,重复步骤1。
- 一直重复以上流程,直到所有路径都被探索完毕,即回退到起点。
在遍历过程中,记得标记已访问的节点,因为不进行标记可能会陷入死循环。标记表示该点已被使用,而清除标记则说明该点可以重新使用。
举例说明:
考虑全排列问题,如字符串 "sai" 的全排列。在DFS中,当枚举到 "s" 时,要标记 "s" 不能再使用(不可能一直 "ssss" 下去),遍历到 "s a" 时,"a" 也不能使用。到 "sai" 时到达尽头,回退到 "s a" 时,要回退 "s",此时 "a" 和 "i" 被解,但是上次指标方向为 "a"(for循环到的位置),下一次要往下一个方向 "i" 组成 "s i",然后 "s i a",依次类推。回退到 "s i" 时,再回退到 "s",下面两个方向都已经枚举过,继续回退。解放了 "s a i",但是第一个方向 "s" 已经走过,从 "a" 开始剩下的步骤依次类推。
在标记时,可以使用boolean数组,true 表示已使用,false 表示未使用。除此之外,也可以使用动态数组List,在使用前删除对应位置元素向下递归,结束后再插入,但效率较低,不推荐使用。
对于上面图片中图的DFS,得到其中一个**DFS搜索的序列(可能有多个)**可以用代码来表示一下:
public class DFSDemo {
static boolean isVisit[];
public static void main(String[] args) {
int map[][]=new int[7][7];
isVisit=new boolean[7];
map[0][1]=map[1][0]=1;
map[0][2]=map[2][0]=1;
map[0][3]=map[3][0]=1;
map[1][4]=map[4][1]=1;
map[1][5]=map[5][1]=1;
map[2][6]=map[6][2]=1;
map[3][6]=map[6][3]=1;
isVisit[0]=true;
DFS(0,map);//从0开始遍历
}
private static void DFS(int index,int map[][]) {
// TODO Auto-generated method stub
System.out.println("访问"+(index+1));
for(int i=0;i<map[index].length;i++){//查找联通节点
if(map[index][i]>0&&isVisit[i]==false){
isVisit[i]=true;
DFS(i,map);
}
}
}
}结合上面的图,大致顺序访问为
访问1
访问2
访问5
访问6
访问3
访问7
访问4
概念:
广度优先搜索(BFS),英文全称为Breadth First Search,是一种不使用经验法则的算法。在该算法中,通过将展开的节点加入到先进先出的队列中,实现对所有可能的子节点的逐层遍历。在典型的实现中,尚未检查的邻居节点被放置在一个称为 "open" 的容器中(例如队列或链表),而已检查过的节点则被放置在 "closed" 容器中。
简单来说,BFS是一种按层遍历的算法,利用队列一层一层地遍历。初次接触BFS可能是在学习数据结构的二叉树层序遍历,之后在图论学习中会遇到更多应用场景。
从路径的角度来看,DFS像一只快速奔跑的疯狗,四处乱咬,走到尽头了就返回其他地方继续;而BFS则像一团毒气,慢慢地扩散开来。
在实现上,朴素的BFS通过控制一个队列,后进先出,进行层序遍历。对于带权值的节点,可能需要使用优先队列。以下是使用邻接表实现BFS遍历的例子:
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
public class BFSDemo {
public static void main(String[] args) {
List<Integer>[] adjacencyList = new ArrayList[7];
boolean[] isVisited = new boolean[7];
for (int i = 0; i < adjacencyList.length; i++) {
adjacencyList[i] = new ArrayList<>();
}
adjacencyList[0].add(1); adjacencyList[0].add(2); adjacencyList[0].add(3);
adjacencyList[1].add(0); adjacencyList[1].add(4); adjacencyList[1].add(5);
adjacencyList[2].add(0); adjacencyList[2].add(6);
adjacencyList[3].add(0); adjacencyList[3].add(6);
adjacencyList[4].add(1);
adjacencyList[5].add(1);
adjacencyList[6].add(2); adjacencyList[6].add(3);
Queue<Integer> queue = new ArrayDeque<>();
queue.add(0);
isVisited[0] = true;
while (!queue.isEmpty()) {
int currentVertex = queue.poll();
System.out.println("访问" + (currentVertex + 1));
for (int i = 0; i < adjacencyList[currentVertex].size(); i++) {
int neighborIndex = adjacencyList[currentVertex].get(i);
if (!isVisited[neighborIndex]) {
queue.add(neighborIndex);
isVisited[neighborIndex] = true;
}
}
}
}
}以上代码使用邻接表实现了一个简单的BFS遍历。在BFS中,使用队列实现先进先出的特性,确保每一层的节点都被遍历。
遍历的结果为:
访问1
访问2
访问3
访问4
访问5
访问6
访问7
BFS当数据达到一定程度,我们使用简单的方法肯定会爆炸的。就可能需要一些特殊的巧妙方法处理,比如剪枝优化、优先队列、A*、DFS套BFS,又或者利用一些非常厉害的数学方法比如康托展开(逆展开)等等。而今天在这里,我们谈谈双向BFS,体验一下算法的奥妙!
适用场景:
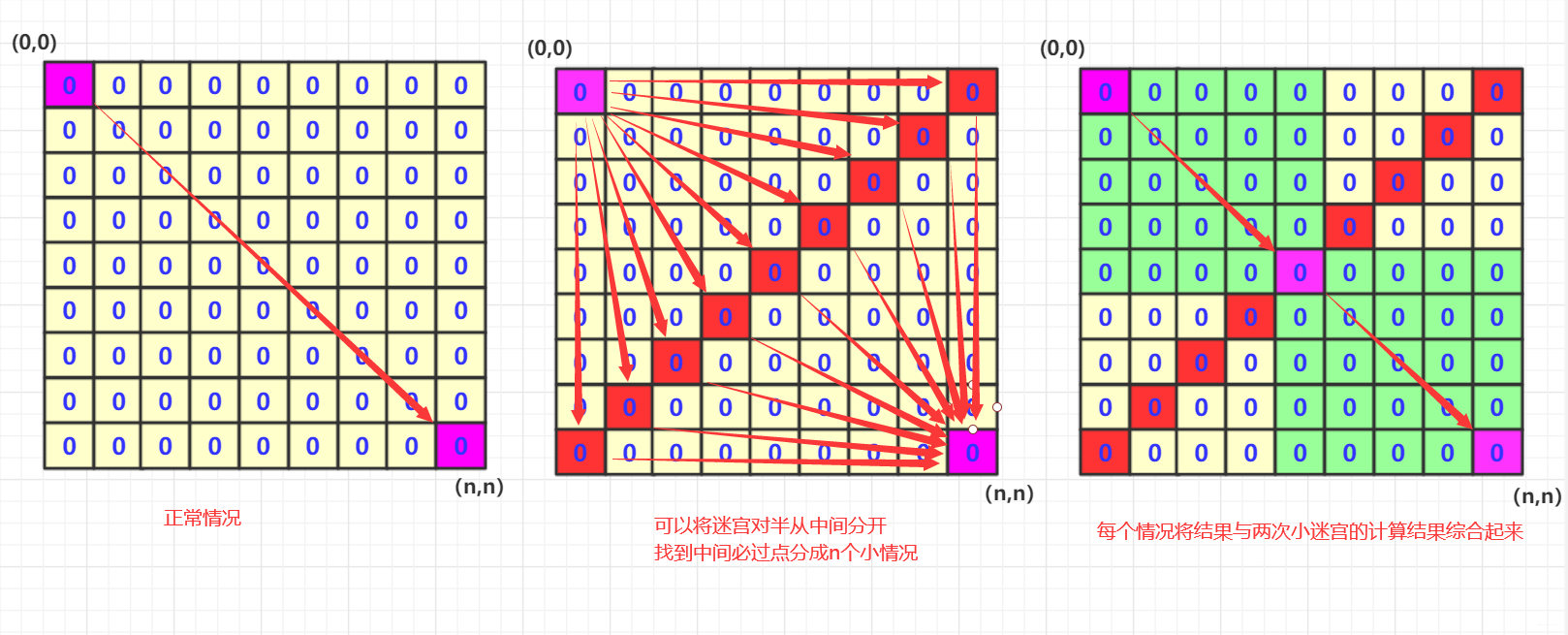
双向广度优先搜索适用于一些问题的拆分,比如在一个迷宫中从左上角到右下角有多少种路径。正常情况下,对整个迷宫进行搜索的复杂度是指数级别的。而通过双向BFS,我们可以将问题拆分为两部分,减少搜索的次数。
原理:
对于一个n x n的迷宫,我们可以将其按照对角线拆分为两个部分。即从左上角到中点的次数为n1,从中点到右下角的次数为n2。总的次数就是n1 * n2。通过这种方式,我们通过乘法减少了加法的运算次数,从而提高了效率。
简单示例:
考虑一个18 x 18的迷宫。如果直接进行全图搜索,复杂度大约是2^18。而使用双向BFS,我们将迷宫拆分成两个9 x 9的部分,总复杂度为2^9,大约是前者的平方根。
优化效果:
从搜索次数的角度来看,如果直接搜索全图的次数是n1 * n2,而使用双向BFS的次数是n1 + n2。如果n1和n2在1000左右,那么两者之间的差距就是平方根级别的。从搜索图形的角度来看,一次全图搜索相当于将一个n x n大小的迷宫转化为n次搜索,每次搜索大约是(n/2) x (n/2)大小的迷宫。因此,如果使用双向BFS,大约是n次搜索,每次搜索是(n/2) x (n/2)大小的迷宫。
总结:
双向广度优先搜索通过问题的拆分,减少了搜索的次数,从而提高了搜索效率。在一些大规模问题中,这种优化方法能够显著降低时间复杂度。
例题实战一下,就拿一道经典双向BFS问题给大家展示一下吧!
题目链接:http://oj.hzjingma.com/contest/problem?id=20&pid=8#problem-anchor
分析:对于题目的要求还是很容易理解的,就是找到所有的路径种类,再判断其中是对称路径的有几个输出即可!
对于一个普通思考是这样的,首先是进行DFS,然后动态维护一个字符串,每次跑到最后判断这个路径字符串是否满足对称要求,如果满足那么就添加到容器中进行判断。可惜很遗憾这样是超时的,仅能通过40%的样例。
接着用普通BFS进行尝试,维护一个node节点,每次走的时候路径储存起来其实这个效率跟DFS差不多依然超时。只能通过40%数据。
接下来就开始双向BFS进行分析!
(1) 既然只能右下,那么对角线的那个位置的肯定是中间的那个字符串的!它的存在不影响是否对称的(n*n的迷宫路径长度为n-1 + n为奇数).
(2) 我们判断路径是否对称,只需要判断从(1,1)到对角节点k(设为k节点)的路径有没有和从(n,n)到k相同的。如果有路径相同的那么就说明这一对构成对称路径
(3) 在具体实现上,我们对每个对角线节点可以进行两次BFS(一次左上到(1,1),一次右下到(n,n)).并且将路径放到两个hashset(set1,set2)中,跑完之后用遍历其中一个hashset中的路径,看看另一个set是否存在该路径,如果存在就说明这个是对称路径放到 总的hashset(set) 中。对角线每个位置都这样判断完最后只需要输出总的hashset(set)的集合大小即可!
ac代码如下:
import java.util.ArrayDeque;
import java.util.HashSet;
import java.util.Queue;
import java.util.Scanner;
import java.util.Set;
public class test2 {
static class node{
int x;
int y;
String path="";
public node() {}
public node(int x,int y,String team)
{
this.x=x;
this.y=y;
this.path=team;
}
}
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
Set<String>set=new HashSet<String>();//储存最终结果
int n=Integer.parseInt(sc.nextLine());
char map[][]=new char[n][n];
for(int i=0;i<n;i++)
{
String string=sc.nextLine();
map[i]=string.toCharArray();
}
Queue<node>q1=new ArrayDeque<node>();//左上的队列
Queue<node>q2=new ArrayDeque<node>();//右下的队列
for(int i=0;i<n;i++)
{
q1.clear();q2.clear();
Set<String>set1=new HashSet<String>();//储存zuoshang
Set<String>set2=new HashSet<String>();//储右下
q1.add(new node(i,n-1-i,""+map[i][n-1-i]));
q2.add(new node(i,n-1-i,""+map[i][n-1-i]));
while(!q1.isEmpty()&&!q2.isEmpty())
{
node team=q1.poll();
node team2=q2.poll();
if(team.x==n-1&&team.y==n-1)//到终点,将路径储存
{
//System.out.println(team2.path);
set1.add(team.path);
set2.add(team2.path);
}
else {
if(team.x<n-1)//可以向下
{
q1.add(new node(team.x+1, team.y, team.path+map[team.x+1][team.y]));
}
if(team.y<n-1)//可以向右
{
q1.add(new node(team.x, team.y+1, team.path+map[team.x][team.y+1]));
}
if(team2.x>0)//上
{
q2.add(new node(team2.x-1, team2.y, team2.path+map[team2.x-1][team2.y]));
}
if(team2.y>0)//左
{
q2.add(new node(team2.x, team2.y-1, team2.path+map[team2.x][team2.y-1]));
}
}
}
for(String va:set1)
{
if(set2.contains(va))
{
set.add(va);
}
}
}
System.out.println(set.size());
}
}本文主要任务是帮助初学者认清DFS和BFS,比较偏基础,但是事实中DFS和BFS比较偏向实战。
对于DFS和BFS,有些区别也有些共性,例如在迷宫很多问题DFS能解决BFS也能解决。
对于DFS一般解决的经典问题有:
- 二叉树的搜索遍历
- 经典全排列、组合、子集问题
- 回溯算法之八皇后问题
- 迷宫搜索问题(能否找到)
- 其他图搜索
而BFS一般解决的问题有:
- 二叉树层序搜索遍历(各种变形例如分层输出、之字形等等空间优化)
- 无权图的最短路径
- 其他迷宫搜索问题(节点带某些权值的)
- 其他问题
当然这里面罗列不全,DFS关注更多的可能是剪枝问题或者记忆化,剪枝就是剪掉没必要的搜索,记忆化就是防止太多重复操作。而BFS关注更多的可能是贪心策略选择(大部分搜索可能有一些附加的条件)可能需要使用优先队列来解决。
DFS和BFS是图论中非常经典的搜索算法,两种算法的重要程度都非常高,这里面主要对其简单介绍,对于普通开发者,能够用DFS和BFS能够解决二叉树问题、迷宫搜索问题等基础简单的就够了(面试官不会那么骚难为你)。
如果理解比较困难,多看教程、多刷题,多刷题之后每做一题算法跑的大概流程是有个数的。