Topic classification

In this repository we explore 3 different techniques for classifying and searching among documents.

• Replicated Softmax Machine (Salakhutdinov, R. & Hinton, G.E. at NIPS 2009)
• Paragraph Vector Distributed Memory (Le, Q.V, and Mikolov, T. at ICML 2014)
• custom Language Model, loosely based off of (Collobert & Weston at ICML 2008)

Create a Replicated Softmax Layer

Create the word representations for original and reconstruction as presented in Jörg Landthaler's Master Thesis and R. Salakhutdinov & G.E. Hinton's Implementation of the Replicated Softmax model.

To obtain a reconstruction we obtain the hidden activation, we denote $D$ the size of the document:

$$D = \sum_{i=1}^n v_{\mathrm{visible}}^{(i)},$$

$$h_{\mathrm{activation}} = \mathrm{sigmoid} \left( v_{\mathrm{visible}} \cdot W

• D \cdot b_{\mathrm{hidden}} \right)$$

The hidden activations can then be used to sample from a multinomial:

$$v_{\mathrm{activation}} = \mathrm{sigmoid} \left( v_{\mathrm{visible}} \cdot W^T + \cdot b_{\mathrm{visible}} \right)$$

The probabilities of each events are obtained using the softmax function:

$$v_{\mathrm{probabilities}}^{(j)} = \frac{\exp(v_{\mathrm{activation}}^{(j)})}{\sum_{i=1}^n \exp(v_{\mathrm{activation}}^{(i)})}$$

And we can now sample:

$$v_{\mathrm{reconstructed}} \sim \mathrm{Mul}\left(n=D, p = v_{\mathrm{probabilities}}\right)$$

We start by importing the library:

import rsm
from daichi_rsm import fmatrix as importer
from daichi_rsm.utils import utils as matrix2text
import numpy as np
import theano as T
import utils
from imp import reload
%matplotlib inline

We can now import data:

datum = importer.parse("sample_data/train")

Let us now test our module:

encoder = rsm.RSM(momentum=0.001, data=datum, hidden_units=123, k=1)
epochs = 200
errors = np.zeros(epochs)
for epoch in range(epochs):
    #if epoch > 0 and epoch % 50 == 0:
    #    encoder.k = int(1 + (float(epoch) / float(epochs)) * 4)
    errors[epoch] = encoder.train()
    #if epoch > 0 and epoch % 10 == 0:
    print("PPL score is %.02f " % errors[epoch])

PPL score is 1322.88 
PPL score is 13431772418765286732989909709094912.00 
...
PPL score is 793.98 
PPL score is 792.10 
PPL score is 790.21 
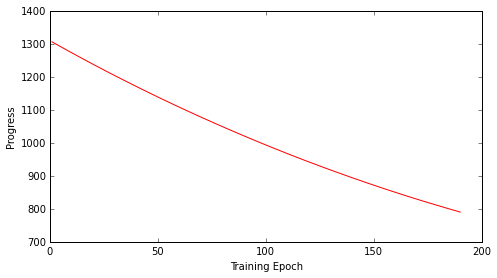
utils.plot_progress(errors[10:])

scaling = datum.sum(axis=1)
reconstructed = encoder.reconstruct(datum)
difference = np.abs(reconstructed - datum).sum()
#fig = plt.figure()
#axes = fig.add_axes([0.1, 0.1, 1.0, 0.8])
#axes.plot(np.linspace(1,len(difference),  len(difference)), difference)
difference
# => 29242.0

Create Word Representation:

reload(utils)

Import associated library:

lexicon, reverse_lexicon = matrix2text.convert_lexicon_file_to_lexicon("sample_data/train.lex")
word_rep = utils.to_word_representation(reverse_lexicon, datum)
word_rep_reconstructed = utils.to_word_representation(reverse_lexicon, reconstructed);

PVDM

Code for this implementation can be found here.

To get it working do the following:

pvdm = PVDM(
    concatenate = True,
    random_window = False,
    workers = 8,
    min_count = 20, # minimun appearance of words to be in vocabulary (modeled)
    window = 10, # size of sentences considered in this model
    batchsize = 1000, # number of paragraphs seen jointly,
    paragraph_size=400, # dimensionality of vector used to represent paragraphs
    decay = False,
    size = 200, # dimensionality of word vectors,
    alpha = 0.035,
    symmetric_window = False, #whether hierarchical softmax task deals with final word or center word
    self_predict= False # whether word to be predicted can help his own case (e.g. "should I pick A | A should be picked?"
)
utils.connect_to_database(database_name = 'yelp')
texts, texts_data = utils.get_some_restaurants(10000, min_words = 400)
pvdm.build_vocab(texts, oov_word = True)

Now we train the PV-DM using gradient descent on the bytes missed during hierachical softmax:

# a push-button fitting function for the words:
pvdm.fit(texts)

This generates a set of vectors for each document (restaurant in this instance), that have a eucledian distance between them related to their content (a distributional model).