1136

1136. Parallel Courses (Medium)

You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given an array relations where relations[i] = [prevCoursei, nextCoursei], representing a prerequisite relationship between course prevCoursei and course nextCoursei: course prevCoursei has to be taken before course nextCoursei.

In one semester, you can take any number of courses as long as you have taken all the prerequisites in the previous semester for the courses you are taking.

Return the minimum number of semesters needed to take all courses. If there is no way to take all the courses, return -1.

 

Example 1:

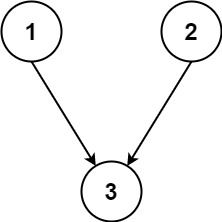
Input: n = 3, relations = [[1,3],[2,3]]
Output: 2
Explanation: The figure above represents the given graph.
In the first semester, you can take courses 1 and 2.
In the second semester, you can take course 3.

Example 2:

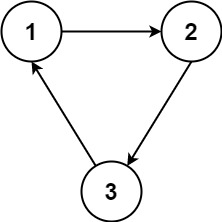
Input: n = 3, relations = [[1,2],[2,3],[3,1]]
Output: -1
Explanation: No course can be studied because they are prerequisites of each other.

 

Constraints:

• 1 <= n <= 5000
• 1 <= relations.length <= 5000
• relations[i].length == 2
• 1 <= prevCoursei, nextCoursei <= n
• prevCoursei != nextCoursei
• All the pairs [prevCoursei, nextCoursei] are unique.

Companies:
Google, Facebook

Related Topics:
Graph, Topological Sort

Similar Questions:

• Course Schedule II (Medium)
• Parallel Courses II (Hard)
• Parallel Courses III (Hard)

Solution 1. Topological Sort (BFS)

// OJ: https://leetcode.com/problems/parallel-courses/
// Author: github.com/lzl124631x
// Time: O(N + E)
// Space: O(N + E)
class Solution {
public:
    int minimumSemesters(int n, vector<vector<int>>& E) {
        vector<vector<int>> G(n);
        vector<int> indegree(n);
        for (auto &e : E) {
            int u = e[0] - 1, v = e[1] - 1;
            G[u].push_back(v);
            indegree[v]++;
        }
        queue<int> q;
        for (int i = 0; i < n; ++i) {
            if (indegree[i] == 0) q.push(i);
        }
        int step = 0, seen = 0;
        while (q.size()) {
            int cnt = q.size();
            seen += cnt;
            while (cnt--) {
                int u = q.front();
                q.pop();
                for (int v : G[u]) {
                    if (--indegree[v] == 0) q.push(v);
                }
            }
            ++step;
        }
        return seen == n ? step : -1;
    }
};

Solution 2. Topological Sort (DFS)

// OJ: https://leetcode.com/problems/parallel-courses/
// Author: github.com/lzl124631x
// Time: O()
// Space: O()
class Solution {
public:
    int minimumSemesters(int n, vector<vector<int>>& E) {
        vector<vector<int>> G(n);
        for (auto &e : E) {
            int u = e[0] - 1, v = e[1] - 1;
            G[u].push_back(v);
        }
        vector<int> state(n, -1); // -1 -> unvisited, 0 -> visiting/invalid, positive number -> visited, depth
        function<int(int)> dfs = [&](int u) {
            if (state[u] != -1) return state[u];
            state[u] = 0;
            int ans = 0;
            for (int v : G[u]) {
                int d = dfs(v);
                if (d == 0) return 0;
                ans = max(ans, d);
            }
            return state[u] = 1 + ans;
        };
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            int depth = dfs(i);
            if (!depth) return -1;
            ans = max(ans, depth);
        }
        return ans;
    }
};