1326

1326. Minimum Number of Taps to Open to Water a Garden (Hard)

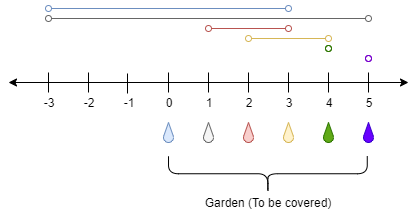
There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e The length of the garden is n).

There are n + 1 taps located at points [0, 1, ..., n] in the garden.

Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.

Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.

 

Example 1:

Input: n = 5, ranges = [3,4,1,1,0,0]
Output: 1
Explanation: The tap at point 0 can cover the interval [-3,3]
The tap at point 1 can cover the interval [-3,5]
The tap at point 2 can cover the interval [1,3]
The tap at point 3 can cover the interval [2,4]
The tap at point 4 can cover the interval [4,4]
The tap at point 5 can cover the interval [5,5]
Opening Only the second tap will water the whole garden [0,5]

Example 2:

Input: n = 3, ranges = [0,0,0,0]
Output: -1
Explanation: Even if you activate all the four taps you cannot water the whole garden.

Example 3:

Input: n = 7, ranges = [1,2,1,0,2,1,0,1]
Output: 3

Example 4:

Input: n = 8, ranges = [4,0,0,0,0,0,0,0,4]
Output: 2

Example 5:

Input: n = 8, ranges = [4,0,0,0,4,0,0,0,4]
Output: 1

 

Constraints:

• 1 <= n <= 10^4
• ranges.length == n + 1
• 0 <= ranges[i] <= 100

Related Topics:
Dynamic Programming, Greedy

Solution 1.

// OJ: https://leetcode.com/problems/minimum-number-of-taps-to-open-to-water-a-garden/
// Author: github.com/lzl124631x
// Time: O(NlogN)
// Space: O(N)
class Solution {
public:
    int minTaps(int n, vector<int>& ranges) {
        vector<pair<int, int>> v;
        for (int i = 0; i < ranges.size(); ++i)
            v.emplace_back(max(0, i - ranges[i]),  min(n, i + ranges[i]));
        sort(v.begin(), v.end());
        int end = 0, newEnd = 0, ans = 0;
        for (int i = 0; i < v.size() && end != n; ++i) {
            if (v[i].first > end) return -1;
            newEnd = max(newEnd, v[i].second);
            if (i + 1 == v.size() || v[i + 1].first > end) {
                end = newEnd;
                ++ans;
            }
        }
        return ans;
    }
};