There is an undirected connected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.
You are given a 0-indexed integer array nums of length n where nums[i] represents the value of the ith node. You are also given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.
Remove two distinct edges of the tree to form three connected components. For a pair of removed edges, the following steps are defined:
- Get the XOR of all the values of the nodes for each of the three components respectively.
- The difference between the largest XOR value and the smallest XOR value is the score of the pair.
- For example, say the three components have the node values:
[4,5,7],[1,9], and[3,3,3]. The three XOR values are4 ^ 5 ^ 7 = 6,1 ^ 9 = 8, and3 ^ 3 ^ 3 = 3. The largest XOR value is8and the smallest XOR value is3. The score is then8 - 3 = 5.
Return the minimum score of any possible pair of edge removals on the given tree.
Example 1:
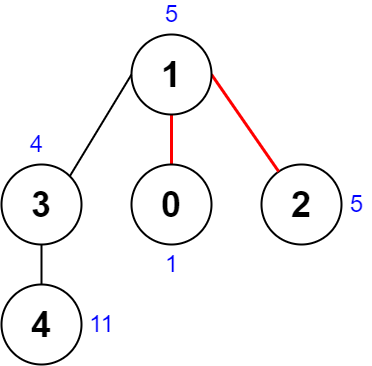
Input: nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]] Output: 9 Explanation: The diagram above shows a way to make a pair of removals. - The 1st component has nodes [1,3,4] with values [5,4,11]. Its XOR value is 5 ^ 4 ^ 11 = 10. - The 2nd component has node [0] with value [1]. Its XOR value is 1 = 1. - The 3rd component has node [2] with value [5]. Its XOR value is 5 = 5. The score is the difference between the largest and smallest XOR value which is 10 - 1 = 9. It can be shown that no other pair of removals will obtain a smaller score than 9.
Example 2:
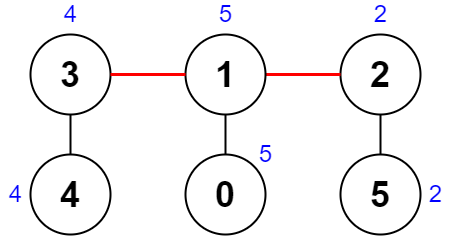
Input: nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]] Output: 0 Explanation: The diagram above shows a way to make a pair of removals. - The 1st component has nodes [3,4] with values [4,4]. Its XOR value is 4 ^ 4 = 0. - The 2nd component has nodes [1,0] with values [5,5]. Its XOR value is 5 ^ 5 = 0. - The 3rd component has nodes [2,5] with values [2,2]. Its XOR value is 2 ^ 2 = 0. The score is the difference between the largest and smallest XOR value which is 0 - 0 = 0. We cannot obtain a smaller score than 0.
Constraints:
n == nums.length3 <= n <= 10001 <= nums[i] <= 108edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedgesrepresents a valid tree.
Companies: Amazon
Related Topics:
Array, Bit Manipulation, Tree, Depth-First Search
Hints:
- Consider iterating over the first edge to remove, and then doing some precalculations on the 2 resulting connected components.
- Will calculating the XOR of each subtree help?
- BFS from all leaf nodes inward. Node
ais a child of nodebifais in the path frombto a leaf node during the BFS. - Use bitmask to track the parent-child relationship.
children[u]is a bitmask of all its children. treeXor[u]is the XOR value of all the nodes in the subtree rooted atu.- Try each pairs of edge
(a,b)and edge(c,d). Based on the parent-child relationships between these 4 nodes, calculate the XOR values of the 3 parts.
// OJ: https://leetcode.com/problems/minimum-score-after-removals-on-a-tree
// Author: github.com/lzl124631x
// Time: O(N^2)
// Space: O(N^2)
// Ref: https://leetcode.com/problems/minimum-score-after-removals-on-a-tree/solutions/2198665/python-3-explanation-with-pictures/
class Solution {
public:
int minimumScore(vector<int>& A, vector<vector<int>>& E) {
int N = A.size(), totalXor = 0;
vector<vector<int>> G(N);
vector<bitset<1000>> children(N);
vector<int> treeXor = A, degree(N), seen(N); // treeXor[u] is the XOR value of all the nodes in the subtree rooted at `u`.
for (auto &e : E) { // Build graph and cound degrees
int u = e[0], v = e[1];
G[u].push_back(v);
G[v].push_back(u);
degree[u]++;
degree[v]++;
}
queue<int> q; // Traverse nodes from all leaves inward
for (int i = 0; i < N; ++i) {
totalXor ^= A[i];
if (degree[i] == 1) q.push(i), seen[i] = 1;
}
while (q.size()) { // Calculate children[u] and treeXor[u]
int u = q.front();
q.pop();
for (int v : G[u]) {
if (seen[v]) continue;
children[v].set(u);
children[v] |= children[u];
treeXor[v] ^= treeXor[u];
if (--degree[v] == 1) {
seen[v] = 1;
q.push(v);
}
}
}
int ans = INT_MAX;
for (int i = 0; i < N - 1; ++i) { // Try the first edge
int a = E[i][0], b = E[i][1];
if (children[a].test(b)) swap(a, b); // Make sure `a` is always a child of `b`.
for (int j = 0; j < i; ++j) { // Try the second edge
int c = E[j][0], d = E[j][1];
if (children[c].test(d)) swap(c, d); // Make sure `c` is always a child of `d`
array<int, 3> score;
if (children[a].test(c)) score = {treeXor[c], treeXor[a] ^ treeXor[c], totalXor ^ treeXor[a] };
else if (children[c].test(a)) score = {treeXor[a], treeXor[a] ^ treeXor[c], totalXor ^ treeXor[c] };
else score = {treeXor[a], treeXor[c], treeXor[a] ^ treeXor[c] ^ totalXor };
ans = min(ans, *max_element(begin(score), end(score)) - *min_element(begin(score), end(score)));
}
}
return ans;
}
};Similar to solution 1, but here we use DFS to calculate treeXor (as X) and children (as C).
// OJ: https://leetcode.com/problems/minimum-score-after-removals-on-a-tree
// Author: github.com/lzl124631x
// Time: O(N^2)
// Space: O(N^2)
class Solution {
public:
int minimumScore(vector<int>& A, vector<vector<int>>& E) {
int N = A.size(), ans = INT_MAX;
vector<vector<int>> G(N);
for (auto &e : E) {
int u = e[0], v = e[1];
G[u].push_back(v);
G[v].push_back(u);
}
vector<int> X(N);
vector<bitset<1000>> C(N);
function<void(int, int)> dfs = [&](int u, int prev) {
X[u] ^= A[u];
C[u].set(u);
for (int v : G[u]) {
if (v == prev) continue;
dfs(v, u);
X[u] ^= X[v];
C[u] |= C[v];
}
};
dfs(0, -1);
for (int i = 0; i < N - 1; ++i) {
int a = E[i][0], b = E[i][1];
if (C[b].test(a)) swap(a, b);
for (int j = 0; j < i; ++j) {
int c = E[j][0], d = E[j][1];
if (C[d].test(c)) swap(c, d);
array<int, 3> v;
if (C[b].test(c)) v = {X[d], X[b] ^ X[d], X[0] ^ X[b]};
else if (C[d].test(a)) v = {X[b], X[d] ^ X[b], X[0] ^ X[d]};
else v = {X[b], X[d], X[0] ^ X[b] ^ X[d]};
ans = min(ans, *max_element(begin(v), end(v)) - *min_element(begin(v), end(v)));
}
}
return ans;
}
};