2646

2646. Minimize the Total Price of the Trips (Hard)

There exists an undirected and unrooted tree with n nodes indexed from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

Each node has an associated price. You are given an integer array price, where price[i] is the price of the ith node.

The price sum of a given path is the sum of the prices of all nodes lying on that path.

Additionally, you are given a 2D integer array trips, where trips[i] = [starti, endi] indicates that you start the ith trip from the node starti and travel to the node endi by any path you like.

Before performing your first trip, you can choose some non-adjacent nodes and halve the prices.

Return the minimum total price sum to perform all the given trips.

 

Example 1:

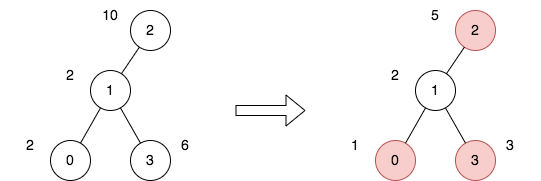
Input: n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
Output: 23
Explanation: The diagram above denotes the tree after rooting it at node 2. The first part shows the initial tree and the second part shows the tree after choosing nodes 0, 2, and 3, and making their price half.
For the 1st trip, we choose path [0,1,3]. The price sum of that path is 1 + 2 + 3 = 6.
For the 2nd trip, we choose path [2,1]. The price sum of that path is 2 + 5 = 7.
For the 3rd trip, we choose path [2,1,3]. The price sum of that path is 5 + 2 + 3 = 10.
The total price sum of all trips is 6 + 7 + 10 = 23.
It can be proven, that 23 is the minimum answer that we can achieve.

Example 2:

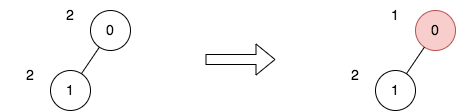
Input: n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
Output: 1
Explanation: The diagram above denotes the tree after rooting it at node 0. The first part shows the initial tree and the second part shows the tree after choosing node 0, and making its price half.
For the 1st trip, we choose path [0]. The price sum of that path is 1.
The total price sum of all trips is 1. It can be proven, that 1 is the minimum answer that we can achieve.

 

Constraints:

• 1 <= n <= 50
• edges.length == n - 1
• 0 <= ai, bi <= n - 1
• edges represents a valid tree.
• price.length == n
• price[i] is an even integer.
• 1 <= price[i] <= 1000
• 1 <= trips.length <= 100
• 0 <= starti, endi <= n - 1

Companies: Adobe, Bloomberg

Related Topics:
Array, Dynamic Programming, Tree, Depth-First Search, Graph

Hints:

• The final answer is the price[i] * freq[i], where freq[i] is the number of times node i was visited during the trip, and price[i] is the final price.
• To find freq[i] we will use dfs or bfs for each trip and update every node on the path start and end.
• Finally, to find the final price[i] we will use dynamic programming on the tree. Let dp(v, 0/1) denote the minimum total price with the node v’s price being halved or not.

Solution 1. Post-order Traversal

1. Build Graph (O(E) time, O(E) space)
2. For each trip, increment the frequency of the nodes in the path. (O(TN) time, O(N) space)
3. DP on tree: Post-order traversal to aggregate the two options (halve, not halve) from leaves to root. The answer is the minimum of (halve, not halve) options of root node.

// OJ: https://leetcode.com/problems/minimize-the-total-price-of-the-trips
// Author: github.com/lzl124631x
// Time: O(E + TN)
// Space: O(E + N)
class Solution {
public:
    int minimumTotalPrice(int n, vector<vector<int>>& E, vector<int>& P, vector<vector<int>>& T) {
        vector<vector<int>> G(n);
        for (auto &e : E) {
            int u = e[0], v = e[1];
            G[u].push_back(v);
            G[v].push_back(u);
        }
        vector<int> cnt(n);
        function<bool(int, int, int)> dfs = [&](int u, int goal, int prev) {
            ++cnt[u];
            if (u == goal) return true;
            for (int v : G[u]) {
                if (v == prev) continue;
                if (dfs(v, goal, u)) return true;
            }
            --cnt[u];
            return false;
        };
        for (auto &t : T) dfs(t[0], t[1], -1);
        function<pair<int, int>(int, int)> dfs2 = [&](int u, int prev) {
            int halve = cnt[u] * P[u] / 2, skip = cnt[u] * P[u];
            for (int v : G[u]) {
                if (v == prev) continue;
                auto [h, s] = dfs2(v, u);
                halve += s;
                skip += min(h, s);
            }
            return pair<int, int>{halve, skip};
        };
        auto [h, s] = dfs2(0, -1);
        return min(h, s);
    }
};