MathJax formula is so small in the PDF output

[jingchangshi]

MathJax formula is so small in the PDF output.
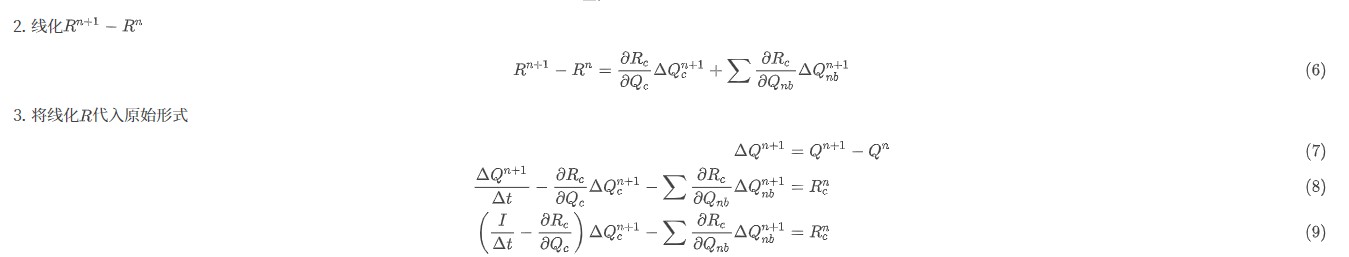
My Typora version is 0.9.77. Windows 10.
The formula in Typora is as follows. It is in the normal size.

The formula in the PDF output is as follows. It is so small.

Thank you for the plugin. It is a helpful project!

[MadMaxChow]

Provide your .md source file, I will try to optimize in VLOOK V9.2.
Thanks for your support!

[jingchangshi]

Here is the source .md file. Thank you!

---
title: 工作日志
---

# BDF1和BDF2的BLUSGS实现

对于微分方程
$$
\frac{\partial Q}{\partial t} = R(Q)
$$


BDF1和BDF2的理论公式如下
$$
\begin{align}
Q^{n+1} - Q^{n} &= \Delta t R^{n+1} \\
Q^{n+1} - \frac{4}{3} Q^{n} + \frac{1}{3} Q^{n-1} &= \frac{2}{3} \Delta t R^{n+1} \\
\end{align}
$$

## BDF1的BLUSGS实现

BLUSGS算法描述见：Sun, Y.; Wang, Z. & Liu, Y. Efficient Implicit Non-linear LU-SGS Approach for Compressible Flow Computation Using High-order Spectral Difference Method, *Comm. Comput. Phys.,* **2009***, 5*, 760-778 

- BDF1的原始形式
  $$
  \begin{align}
  \frac{ Q^{n+1} - Q^{n} }{\Delta t} &= R^{n+1} \\
  \frac{ Q^{n+1} - Q^{n} }{\Delta t} - \left ( R^{n+1} - R^{n} \right ) &= R^{n} \\
  \end{align}
  $$
  
- 线化$R^{n+1}-R^{n}$
  $$
  \begin{align}
  R^{n+1} - R^{n} = \frac{\partial R_c}{\partial Q_c} \Delta Q^{n+1}_c + \sum \frac{\partial R_{c}}{\partial Q_{nb}} \Delta Q^{n+1}_{nb}
  \end{align}
  $$
  
- 将线化$R$代入原始形式
  $$
  \begin{align}
  \Delta Q^{n+1} &= Q^{n+1} - Q^{n} \\
  \frac{ \Delta Q^{n+1} }{\Delta t} - \frac{\partial R_c}{\partial Q_c} \Delta Q^{n+1}_c - \sum \frac{\partial R_{c}}{\partial Q_{nb}} \Delta Q^{n+1}_{nb} &= R^n_c \\
  \left ( \frac{ I }{\Delta t} - \frac{\partial R_c}{\partial Q_c} \right ) \Delta Q^{n+1}_c - \sum \frac{\partial R_{c}}{\partial Q_{nb}} \Delta Q^{n+1}_{nb} &= R^n_c \\
  \end{align}
  $$
  
- Gauss-Seidel加速
  $$
  \begin{align}
  \left ( \frac{ I }{\Delta t} - \frac{\partial R_c}{\partial Q_c} \right ) \Delta Q^{k+1}_c - \sum \frac{\partial R_{c}}{\partial Q_{nb}} \Delta Q^{k}_{nb} &= R^n_c \\
  \Delta Q^{k+1}_c &= Q^{k+1} - Q^{n} \\
  \end{align}
  $$
  
- 再次线化$R^{k}-R^{n}$
  $$
  R^{k} - R^{n} = \frac{\partial R_c}{\partial Q_c} \Delta Q^{k}_c + \sum \frac{\partial R_{c}}{\partial Q_{nb}} \Delta Q^{k}_{nb}
  $$
  
- 将线化$R$代入，整理
  $$
  \begin{align}
  \left ( \frac{ I }{\Delta t} - \frac{\partial R_c}{\partial Q_c} \right ) \Delta Q^{k+1}_c &= R^k_c - \frac{\partial R_{c}}{\partial Q_{c}} \Delta Q^{k}_{c} \\
   &= R^k_c + \left ( \frac{ I }{\Delta t} - \frac{\partial R_c}{\partial Q_c} \right ) \Delta Q^{k}_{c} - \frac{ I }{\Delta t} \Delta Q^{k}_{c} \\
  \left ( \frac{ I }{\Delta t} - \frac{\partial R_c}{\partial Q_c} \right ) \left ( \Delta Q^{k+1}_c - \Delta Q^{k}_{c} \right ) &= R^k_c - \frac{ I }{\Delta t} \Delta Q^{k}_{c} \\
  \left ( \frac{ I }{\Delta t} - \frac{\partial R_c}{\partial Q_c} \right ) \tilde{\Delta} Q^{k+1}_c &= R^k_c - \frac{ I }{\Delta t} \Delta Q^{k}_{c} \\
  \tilde{\Delta} Q^{k+1}_c &= Q^{k+1}_c - Q^{k}_c \\
  \end{align}
  $$
  

最后两个方程是最终的BDF1的BLUSGS实现。

## BDF2的BLUSGS实现

BDF2的实现与BDF1类似。

- BDF2的原始形式
  $$
  \begin{align}
  \frac{ Q^{n+1} - \frac{4}{3} Q^{n} + \frac{1}{3} Q^{n-1} }{ \frac{2}{3} \Delta t } &= R^{n+1} \\
  \frac{3}{2} \left ( \frac{ \Delta Q^{n+1} }{ \Delta t } - \frac{1}{3} \frac{ \Delta Q^{n} }{ \Delta t } \right ) - \left ( R^{n+1} - R^{n} \right ) &= R^{n} \\
  \Delta Q^{n+1} &= Q^{n+1} - Q^{n} \\
  \end{align}
  $$
  
- 线化$R^{n+1}-R^{n}$
  $$
  \begin{align}
  R^{n+1} - R^{n} = \frac{\partial R_c}{\partial Q_c} \Delta Q^{n+1}_c + \sum \frac{\partial R_{c}}{\partial Q_{nb}} \Delta Q^{n+1}_{nb}
  \end{align}
  $$
  
- 将线化$R$代入原始形式
  $$
  \begin{align}
  \left ( \frac{3}{2} \frac{ I }{\Delta t} - \frac{\partial R_c}{\partial Q_c} \right ) \Delta Q^{n+1}_c - \frac{1}{2} \frac{ I }{\Delta t} \Delta Q^{n}_c - \sum \frac{\partial R_{c}}{\partial Q_{nb}} \Delta Q^{n+1}_{nb} &= R^n_c \\
  \end{align}
  $$
  
- Gauss-Seidel加速
  $$
  \begin{align}
  \left ( \frac{3}{2} \frac{ I }{\Delta t} - \frac{\partial R_c}{\partial Q_c} \right ) \Delta Q^{k+1}_c - \frac{1}{2} \frac{ I }{\Delta t} \Delta Q^{n}_c - \sum \frac{\partial R_{c}}{\partial Q_{nb}} \Delta Q^{k}_{nb} &= R^n_c \\
  \Delta Q^{k+1}_c &= Q^{k+1} - Q^{n} \\
  \end{align}
  $$
  
- 再次线化$R^{k}-R^{n}$
  $$
  R^{k} - R^{n} = \frac{\partial R_c}{\partial Q_c} \Delta Q^{k}_c + \sum \frac{\partial R_{c}}{\partial Q_{nb}} \Delta Q^{k}_{nb}
  $$
  
- 将线化$R$代入，整理
  $$
  \begin{align}
  \left ( \frac{3}{2} \frac{ I }{\Delta t} - \frac{\partial R_c}{\partial Q_c} \right ) \Delta Q^{k+1}_c - \frac{1}{2} \frac{ I }{\Delta t} \Delta Q^{n}_c &= R^k_c - \frac{\partial R_{c}}{\partial Q_{c}} \Delta Q^{k}_{c} \\
   &= R^k_c + \left ( \frac{3}{2} \frac{ I }{\Delta t} - \frac{\partial R_c}{\partial Q_c} \right ) \Delta Q^{k}_{c} - \frac{3}{2} \frac{ I }{\Delta t} \Delta Q^{k}_{c} \\
  \left ( \frac{3}{2} \frac{ I }{\Delta t} - \frac{\partial R_c}{\partial Q_c} \right ) \left ( \Delta Q^{k+1}_c - \Delta Q^{k}_{c} \right ) - \frac{1}{2} \frac{ I }{\Delta t} \Delta Q^{n}_c &= R^k_c - \frac{3}{2} \frac{ I }{\Delta t} \Delta Q^{k}_{c} \\
  \left ( \frac{3}{2} \frac{ I }{\Delta t} - \frac{\partial R_c}{\partial Q_c} \right ) \tilde{\Delta} Q^{k+1}_c &= R^k_c - \frac{3}{2} \frac{ I }{\Delta t} \Delta Q^{k}_{c} + \frac{1}{2} \frac{ I }{\Delta t} \Delta Q^{n}_c \\
  \left ( \frac{3}{2} \frac{ I }{\Delta t} - \frac{\partial R_c}{\partial Q_c} \right ) \tilde{\Delta} Q^{k+1}_c &= R^k_c - \frac{1}{2 \Delta t} \left ( 3 I Q^{k}_{c} - 4 I Q^{n}_c + I Q^{n-1}_c \right ) \\
  \tilde{\Delta} Q^{k+1}_c &= Q^{k+1}_c - Q^{k}_c \\
  \end{align}
  $$
  

最后两个方程是最终的BDF2的BLUSGS实现。

[MadMaxChow]

The problem you said will be fixed in Version 9.2. Should be released in the next two weeks.

[jingchangshi]

The problem you said will be fixed in Version 9.2. Should be released in the next two weeks.

Thank you!