maximum-product-of-splitted-binary-tree

< Previous 　　　　　　　　　　　　　　　　 Next >

1339. Maximum Product of Splitted Binary Tree (Medium)

Given a binary tree root. Split the binary tree into two subtrees by removing 1 edge such that the product of the sums of the subtrees are maximized.

Since the answer may be too large, return it modulo 10^9 + 7.

 

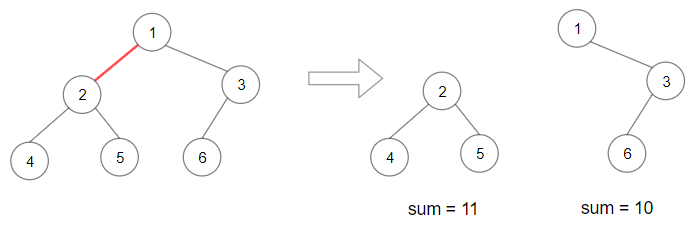
Example 1:

Input: root = [1,2,3,4,5,6]
Output: 110
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)

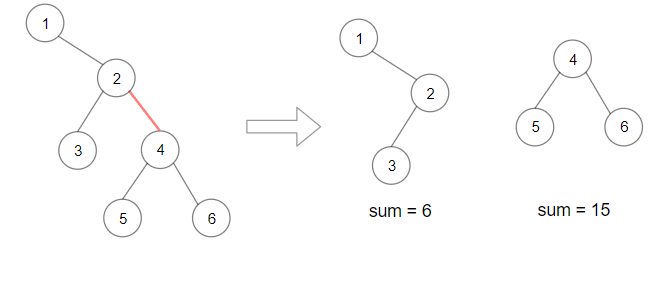
Example 2:

Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90
Explanation:  Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)

Example 3:

Input: root = [2,3,9,10,7,8,6,5,4,11,1]
Output: 1025

Example 4:

Input: root = [1,1]
Output: 1

 

Constraints:

• Each tree has at most 50000 nodes and at least 2 nodes.
• Each node's value is between [1, 10000].

Related Topics

[Tree] [Dynamic Programming]

Hints

Hint 1

If we know the sum of a subtree, the answer is max( (total_sum - subtree_sum) * subtree_sum) in each node.