Angle Graph Method for High School Geometry

[sylee957]

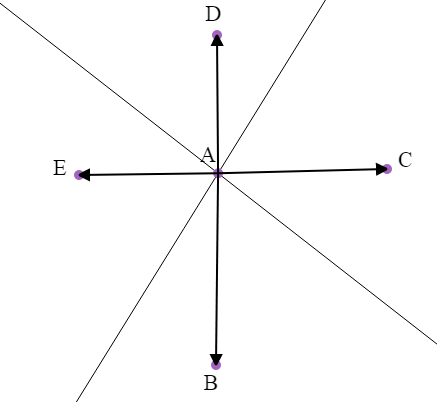
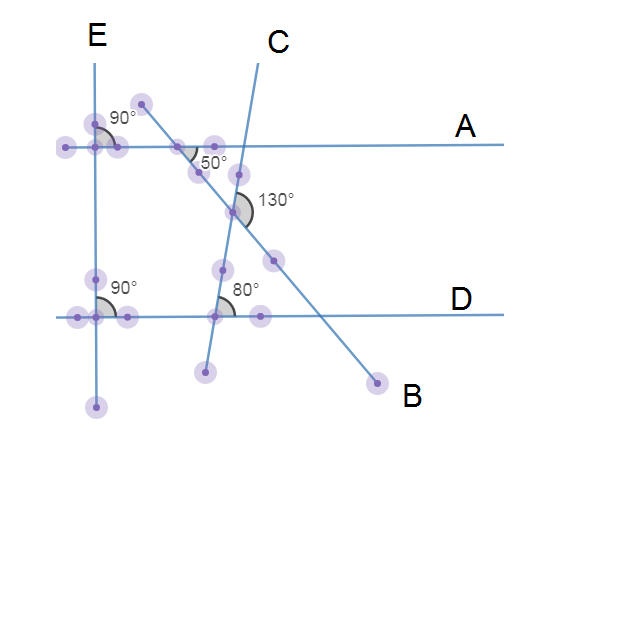
There are many precollege level geometry problems that questions about computing angles from the given diagram defined by segments, lines, predefined angles and angle bisector relationships between segments or lines.
However, unlike carried by hand, it is not obvious about how to carry out the arithmetic of angles in the diagram in computational way, because the geometry problems imposes mutual relationships between angles, and even the diagram itself looks hard to represent as a symbolic object because most of the elementary geometry problems are coordinate-free.

In most of the preceding studies about solving plane geometry problems (Area Method, Wu Method, ...), they rather transforms angles into trigonometric functions, which is very inefficient for solving problems that involves numeric degrees that are not special angles (like 43 degrees, ... that uses 1 degree as its unit), and also have problems that computing the inverse trigonometric functions are not easy to compute.

In ¹, it proposes a method called 'Angle Graph' to find the evaluation order of the angles, and angles can be evaluated linearly like done by the students.
I'd note that some geometric proofs needs 'auxiliary lines' and this method can't deal with such proofs. However, if the user supplies the auxiliary line first to the method as input preprocessing, this can still help more difficult proofs.
I add the implementation code in sympy below. The definitions and the mathematical details can be consulted from ¹

Code

from sympy import *


def angle_graph(V, A, B):
    def eliminable_vertex(v, A, B):
        d = 0
        edge = (v,)
        for a, b in A:
            if v in (a, b):
                edge = (a, b)
                d += 1
        for a, b, c in B:
            if v in (a, b, c):
                edge = (a, b, c)
                d += 1
                
        if d in (0, 1):
            return edge
    
    V = list(V)
    A = dict(A)
    B = dict(B)
    
    elim = []
    while True:
        for v in V:
            e = eliminable_vertex(v, A, B)
            if e is not None:
                break
        else:
            break
        
        if len(e) == 1:
            elim.append(("ES1", v))
            V.remove(v)
            continue
        elif len(e) == 2:
            if v == e[0]:
                elim.append(("ES2A", v, e[1], A[e]))
            elif v == e[1]:
                elim.append(("ES2B", v, e[0], A[e]))
            V.remove(v)
            A.pop(e)
            continue
        elif len(e) == 3:
            if v == e[0]:
                elim.append(("ES3B", v, e[2], e[1], B[e]))
            elif v == e[1]:
                elim.append(("ES3B", v, e[2], e[0], B[e]))
            elif v == e[2]:
                elim.append(('ES3A', v, e[0], e[1], B[e]))
            V.remove(v)
            B.pop(e)
            continue
    
    if V:
        raise ValueError
    
    angles = {}
    new_symbols = []
    i = 0
    for label, *args in reversed(elim):
        if label == "ES1":
            v, = args
            angles[v] = Dummy(f'\phi_{i}')
            new_symbols.append(angles[v])
            i += 1
        elif label == "ES2A":
            a, b, diff = args
            angles[a] = angles[b] - diff
        elif label == "ES2B":
            a, b, diff = args
            angles[a] = angles[b] + diff
        elif label == "ES3A":
            a, b, c, n = args
            angles[a] = (angles[b] + angles[c] + n * pi) / 2
        elif label == "ES3B":
            a, b, c, n = args
            angles[a] = 2 * angles[b] - angles[c] - n * pi
    return angles, new_symbols


def angle_between(directions, a, b, sa, sb):
    if sa == 1 and sb == 1: 
        return directions[b] - directions[a]
    elif sa == 1 and sb == -1:
        return pi + angle_between(directions, a, b, 1, 1)
    elif sa == -1 and sb == 1:
        return pi + angle_between(directions, a, b, 1, 1)
    elif sa == -1 and sb == -1:
        return angle_between(directions, a, b, 1, 1)

Elementary Examples

1. Sum of angles of triangle

V = ["A", "B", "C"]
A = {}
B = {}

directions, dummies = angle_graph(V, A, B)
result = \
    angle_between(directions, 'A', 'C', 1, -1) + \
    angle_between(directions, 'B', 'A', 1, -1) + \
    angle_between(directions, 'C', 'B', 1, -1)

print(Mod(result, 2*pi))
# pi

Although the result looks strange that it just throws out three free symbols as directions, the proof is still mathematically correct because you need orient some lines backwards to correctly identify with the inner angles.
The good point is that it doesn't need to be aware that the object is explicitly defined like Triangle, but angle relation of triangle can automatically be picked up from the three lines of the plane by using algebra of directions.

Similarly, the sum of angles of a n-gon is naturally embedded into the algebra, but the only problem is that the computation is done modulo 2*pi which makes the sum of angles of rectangle 0 than 2*pi and the sum of the angles of pentagon as pi.
However, it is a natural problem of the Euclidean geometry that 0 degree and 360 degree can't be distinguished on the diagram, and has no problem for solving problems like discovering the remaining angle given other angles of the polygon.

2. Angles of isosceles triangle

V = ["A", "B", "C", 'D']
A = {('D', 'C'): pi/2}
B = {('A', 'B', 'D'): 0}

directions, dummies = angle_graph(V, A, B)

print(Mod(angle_between(directions, 'C', 'A', 1, -1), 2*pi))
print(Mod(angle_between(directions, 'B', 'C', -1, -1), 2*pi))

The definition of isosceles triangle is not integrated to the framework, but when you have identified that three orientations A, B, C should form an isosceles triangle, you can add an auxiliary orientation D as an angle bisector of A, B and define an additional relation that the angle between D and C are 90 degrees.
Similarly, if you identify that the two line segments (with respect to the orientations A, B) are equal, you can reformulate this by defining an auxiliary orientation C which can reformulate the problem as the isosceles triangle problem, and adding the auxiliary angle bisector as above.

3. Inscribed angle theorem

V = ["A", "B", "C", 'U', 'V', 'W', 'X', 'Y', 'Z']
A = {('X', 'U'): -pi/2, ('Y', 'V'): pi/2, ('Z', 'W'): -pi/2}
B = {('C', 'A', 'U'): 0, ('A', 'B', 'V'): 0, ('B', 'C', 'W'): 0}

directions, dummies = angle_graph(V, A, B)
print(Mod(angle_between(directions, 'Z', 'Y', 1, 1), 2*pi))
print(Mod(angle_between(directions, 'C', 'A', 1, 1), 2*pi))

Inscribed angle theorem can be embedded by using the three isosceles triangle above

Some Examples

1. Computing angle from star
   https://mindyourdecisions.com/blog/2016/12/11/solving-for-the-angle-in-a-star-sunday-puzzle/

V = ["A", "B", "C", 'D', 'E']
A = {('A', 'B'): pi*4/18, ('A', 'C'): pi*11/18, ('B', 'D'): pi*10/18}
B = {}

directions, dummies = angle_graph(V, A, B)
print(Mod(angle_between(directions, 'C', 'D', 1, 1), 2*pi))

Limitations

This method may need more example that can demonstrate that it can be used with solve more trickier problems
Also this can only be able to solve the geometry problems where the construction is not 'overdetermined', for example, if three angles of a triangle are constructed before, all vertex of the graph have degree 2, so you may have to remove some redundant constants if this stops working.

References

Footnotes

1. Todd, P. A Symbolic Dynamic Geometry System Using the Analytical Geometry Method. Math.Comput.Sci. 14, 693–726 (2020). https://doi.org/10.1007/s11786-020-00490-0 ↩ ↩²

[smichr]

geometric proofs needs 'auxiliary lines'

For those rusty but interested: do you mean cases like these?

[smichr]

@sylee957 , What is the meaning of 0 in B = {('A', 'B', 'D'): 0}?

[sylee957]

The ‘(a, b, c): 0’ should mean that ‘c’ is the ‘0’th bisector of ‘a’ and ‘b’
If it is 1, 2, 3, then it would mean that c is the bisector rotated 90 degrees counterclockwise 1, 2, 3 times

[smichr]

@sylee957 , thanks -- so imagine lines crossing at a point and you are indicating in which direction the bisector eminates.

From what you have in the example above it looks like the "0" one is the one in the same direction as the oriented lines

[smichr]

I'm getting an unexpected answer for the crossing angle here:

>>> V='abcde'
>>> A={tuple(i):j for i,j in (('ba',rad(50)),('cd',rad(80)),('ae',pi/2),
...     ('de',pi/2))}
>>> B={}
>>> d, s = angle_graph(V,A,B)
>>> deg(angle_between(d, 'b', 'c', 1, 1))
-30

[sylee957]

I don’t have computer now to verify this, but ‘cd’ could be changed to ‘dc’. The angle should be defined as counterclockwise angle from the start oriented line to the end oriented line.

[smichr]

>>> A={tuple(i):j for i,j in (('ba',rad(50)),('dc',rad(80)),('ae',pi/2),
...     ('de',pi/2))}
>>> B={}
>>> d, s = angle_graph(V,A,B)
>>> deg(angle_between(d, 'b', 'c', 1, 1))
130

So use the right hand rule to define angles.