| course |
course_year |
question_number |
tags |
title |
year |
Markov Chains |
IB |
43 |
|
Paper 1, Section II, 19H |
2021 |
Let $\left(X_{n}\right){n \geqslant 0}$ be a Markov chain with transition matrix $P$. What is a stopping time of $\left(X{n}\right)_{n \geqslant 0}$ ? What is the strong Markov property?
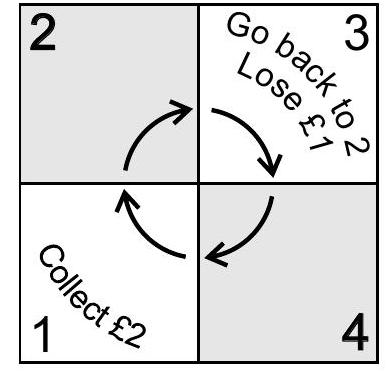
The exciting game of 'Unopoly' is played by a single player on a board of 4 squares. The player starts with $£ m$ (where $m \in \mathbb{N}$ ). During each turn, the player tosses a fair coin and moves one or two places in a clockwise direction $(1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 1)$ according to whether the coin lands heads or tails respectively. The player collects $£ 2$ each time they pass (or land on) square 1. If the player lands on square 3 however, they immediately lose $£ 1$ and go back to square 2. The game continues indefinitely unless the player is on square 2 with $£ 0$, in which case the player loses the game and the game ends.

(a) By setting up an appropriate Markov chain, show that if the player is at square 2 with $£ m$, where $m \geqslant 1$, the probability that they are ever at square 2 with $£(m-1)$ is $2 / 3 .$
(b) Find the probability of losing the game when the player starts on square 1 with $£ m$, where $m \geqslant 1$.
[Hint: Take the state space of your Markov chain to be ${1,2,4} \times{0,1, \ldots}$.]