Assignment 2

1. AHU, 1.3-1.4
2. Miller and Boxer, Chapter 1, Problem 2
3. In practice, many matrix computations involve sparse matrices. Data structures for storing sparse vectors and matrices store only the nonzero entries. Although this requires storing not only the values of the nonzeros, but their location within the vector/matrix, it is usually still more memory efficient to use such data structures than to explicitly store all matrix entries. This problem examines some of the details of the efficiency of these data structures. In a future assignment, you will be asked to build on what you do here and empirically test matrix multiplication methods using your data structures.
   1. Implement and document a sparse matrix data structure in Julia. You should support both CSC and CSR formats (you can research what these stand for and how they work). You should include methods for converting to/from dense matrices by implementing the copyto() method. You should also support in-place convertion t/from CSC and CSR, as well as computing the transpose. Implement a series of tests to demonstrate your implementation is working as expected (generate random matrices, convert in different ways, ensure the results are the same, etc.)
   2. Do a theoretical comparison of the efficiency with which such a sparse matrix can be initialized with random elements versus that with which a dense matrix can be initialized. Derive the appropriate running time functions under the assumptions of the RAM model, which means you don't need to take into account cache effects. You will need to account for the density of the matrix in your analysis.
   3. Verify your analysis from the previous part empirically.
   4. Give a pseudocode implementation of a function for multiplying two matrices stored in your sparse representation. You will need several versions, depending on whether each of the matrices is stored in CSR or CSC format. Analyze the efficiency of your sparse matrix multiplication (again, in the RAM model without taking cahceh effects into account) and compare it to the efficiency with which the same operation can be performed on two dense matrices.
   5. Is there any way to take cache effects into account in implementing sparse matrix multiplication? What are the differences (if any) from the case with explicitly stored matrices?
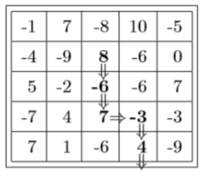
4. Valkin's Mile is a solitaire game played on an $n \times n$ square grid in which each grid square contains an integer (positive or negative). The player starts in any chosen square and the may move either right or down in each turn until some move results in exiting the board. The score for a given sequence is the sum total of the values of all squares in the path. For example, the sequence shown below would result in the score 8-6+7-3+4 = 10 (this is not the best possible score on this board).

   

   1. Write pseudo-code for an algorithm to determine the maximum score for a given board as efficiently as possible (hint: use recursion). In part (c), you will need to prove that the running time of your algorithm cannot be made any more efficient so think carefully about whether your algorithm can be improved. You must justify (at least informally) that your algorithm is correct.
   2. Determine the running time of your algorithm.
   3. Explain why your algorithm is asympototically optimal (obviously, this means that your algorithm should actually be asymptotically optimal, which the naive versions are not).