New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Fourier-Hankel implementation for direct and inverse Abel transforms #24
Comments
|
Yes, it would be fun to include the FH version of the transform for comparison purposes! The So, I think that we may need to use that package that you suggest, or figure something else out. |
|
This should be pretty easy to implement, but, when I looked around the literature, I could not find a clear equation for the Fourier-Hankel transform, despite it being mentioned frequently. @stggh, do you know of a paper that gives the equation/algorithm for the FH transform? |
|
Python code for the Hankel transform is available at this github. The HankelTransform function requires a function (image) input rather than (grid) data. At the moment I am confused by the evaluation of the Hankel transform in radial (1D) space, and how to return the 2D image, although, the (slightly buggy) examples appear to cover this case. Thoughts, suggestions? |
|
Oh, that is pretty cool that you found code for the Hankel transform. It looks like that code is just for the 1D case, right? We would just need to loop over all rows (or, hopefully, vectorize somehow). It looks like that package was developed reasonably recently, so the author might be able to help us wrangle it into a Fourier-Hankel transform function. |
|
@DanHickstein my apologies for the delay in my response. My coding time is limited at the moment, due to an upcoming teaching semester. @steven-murray author of the hankel is very helpful. I just have not had time to work through the 2D implementation, but will do so, once I have some free time. |
|
Hi there, Would love to figure out how to get Having briefly read through this thread -- it seems like you need a 2D image. My code will of course do this fine if the image is radially symmetric. I have never considered a case where there is not radial symmetry (radial symmetry is usually the reason you'd use a hankel transform in the context of a FT). Just let me know what you need and I should be able to help out pretty easily. Cheers. |
|
Hmmm, so is a 2D FT required, or a 1D FT over each row? |
|
@steven-murray, Thanks for being willing to help us out! Everything happens in 1D. And, conceptually, each row can be treated separately. When @stggh says that we want to avoid iterating "row-by-row", he is pointing that, to achieve the highest efficiency, we need to avoid for loops in Python, and instead vectorize our calculations using 2D numpy arrays. (So, there are still for loops, but they are just getting done by the c-code in numpy). Anyway, for a proof-of-principle demonstration, it's totally fine to iterate over the rows in Python, as far as I am concerned. We can figure out how to speed things up after we get reasonable results. Big picture: the "Fourier-Hankel" transform is mentioned in many papers about Abel transform as something of the "1980's gold standard" that has now been improved upon. We always thought that PyAbel should include it, because everyone talks about it so much, but we never really knew a good implementation of the Hankel transform, and I'm not sure that I ever really found a paper that explains how this "Fourier-Hankel" transform should be completed. This thesis seems to say that we just need to take an inverse Hankel transform of the FT of our data:
I am curious to see how the FH transform compares with the other methods. It may offer a different efficiency scaling with the image size, and may be able to handle larger images. And it may offer an advantage in that it doesn't need to pre-compute and basis-sets like many of the other transform methods. |
|
I agree our main aim is to implement the F-H transform (and if possible improve the execution speed), and Eq. (2.7) appears correct, according to @rth's FHA cycle top comment:
As @DanHickstein states, we process each row, Fourier transform and then inverse Hankel transform. |
|
Okay cool. Well, This is why I'm wondering if there's a reason you don't want to use the basic "Direct HT" given in Eq. 2.12 of the thesis you shared? It would be easy to implement, easy to vectorize, and probably faster than I'm assuming that you start the problem only with a discrete 2D array, not an analytic function? |
Bummer! Sorry, that I did not realise this.
Path of least pain ;-) Eq. 2.12 requires a little thought. |
|
I have been thinking about implementing some discrete HT functions in I should clarify my last comment -- Here's a small implementation of the DHT that I just wrote (it seems to work on a simple Gaussian function): from scipy.special import jn
import numpy as np
from numpy.fft import fft, hfft, fftfreq, fftshift
def construct_dht_matrix(N, nu = 0, b = 1):
m = np.arange(0,N).astype('float')
n = np.arange(0,N).astype('float')
return b * jn(nu, np.outer(b*m, n/N))
def dht(X, d = 1, nu = 0, axis=-1, b = 1):
N = X.shape[axis]
prefac = d**2
m = np.arange(0,N)
freq = m/(float(d)*N)
F = construct_dht_matrix(N,nu,b)*m
return prefac * np.tensordot(F,X, axes=([1],[axis])), freqThis works for arbitrary dimension matrix I tried also writing the Abell transform, as specified by Eq. 2.13 in the thesis. I'm getting something slightly wrong (probably the frequency normalisation), but the code I have thus far is def hankel_fourier_transform(X, d=1, nu = 0):
N = X.shape[-1] # Assuming we're doing transform on second axis (X is 2D here)
# Assumes X is 2D and has symmetry about 0
G = np.real(fftshift(fft(X, axis=-1))[:,N/2:]*d) # Just get non-negative frequencies
# Now the DHT
eps = dht(G, d=1/(N*d), nu=nu, b=np.pi)[0] * 2 #b=pi to account for N/2, then *2 to get 2pi out front
return eps, d*np.arange(0,N/2)Feel free to play around with these. Doing this has sparked some ideas for things to implement in |
|
@steven-murray fantastic - great work! I can confirm the Gaussian discrete Hankel transform, although I am also not sure about the normalization. For the inverse Abel transform we pass 1/2 image row (right-side), a 1d-numpy array. This may then duplicated for the (r)fft Testing this for inverse Abel transform |
|
Some progress, but the profile is overcorrected. very poor coding here |
|
Thanks @stggh , this looks promising -- certainly using the zeros of the Bessel function is more akin to the way that I don't have much time this week as I am away for a conference, but will plug away at it when I can. |
Actually, this time I just used Wolfram|Alpha on each term separately :-) |
|
The "trick" for the Hankel transform is that the source function is evaluated at the spherical Bessel function zeros. A radial range More later, at this moment I am also time poor. |
|
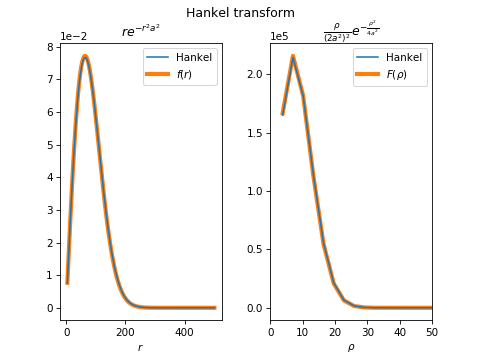
This code gist appears to correctly (forward, inverse) transform the Baddour analytical exponential transform pairs. This image shows the numerical transform with its analytical function: The only issue appears to be the need to sample our |
|
Improved version of the transformation_matrix: def transformation_matrix(jz, nu=0):
# Baddour transformation matrix Eq. (25) JOSA A32, 611-622 (2015)
b = 2/(jn(nu+1, jz) * jn(nu+1, jz) * jz[-1])
return b * jn(nu, np.outer(jz, jz / jz[-1]))Updated code gist |
|
This all looks really good. It is frustrating that a re-sampling has to be performed, It would be nice to be able to directly use an input discrete array. I'm trying to think of a way around this, but can't at this point (my own We could perhaps build a reasonably robust case-by-case system in which an input array is interpolated onto the correct grid. It would be hard to vectorize well though, and interpolation always turns up problems for bad functions. I might give it a shot this afternoon, and add a few tests in as well. |
|
I find the sample space selection confusing. I think the required sampling condition is in fact the product This gist is the Baddour sinc function test, Eq.s (84, 85). The above condition gives @steven-murray thanks for keeping a tag on this. I am sure you understand much more about these transform sample spaces that I do. I agree, interpolation of each image row intensity will be necessary, but perhaps there is some clever @DanHickstein |
|
Image interpolation is not a good idea because of the measurement noise. We may as well return to the discrete version of the basic definition: and @steven-murray original code above, which, I think(?), is the a fast version of Whittaker C-code Imaging in Chemical Dynamics, that I converted to Python (below). This Hankel transform operates on each image row, without requiring interpolation. def Hankel(F, nu=0):
"""
Whitaker "Image reconstruction: the Abel transform" Ch 5
Parameters
----------
F : numpy 1D array
image row
Returns
-------
f : numpy 1D array
Hankel transform
"""
n = F.size
Nyquist = 1/(2*n)
f = np.zeros_like(F)
for i in range(n):
for j in range(n):
q = Nyquist*j
f[i] += q*F[j]*jn(nu, 2*np.pi*q*i)
return fI will play some more. Sorry, for the diversion into the Baddour algorithm, which appears more suitable for analytical functions. |
|
Vectorized Whitaker code: n = F.size
Nyquist = 1/(2*n)
f = np.zeros_like(F)
i = np.arange(n)
for j in range(n):
q = Nyquist*j
f[:] += q*F[j]*jn(nu, 2*np.pi*q*i[:])
return fNot sure about frequency axis or amplitude scaling. @steven-murray |
|
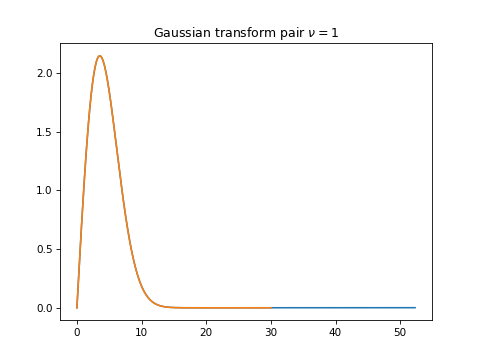
The @steven-murray version of the Hankel transform is good, equivalent to, but faster than, Whitaker's and they both pass the Baddour analytical function (Gaussian, Sinc) transform pair test. The issue of the Fourier-Hankel transform of curve A (above) remains. |
|
discrete Fourier transform Sorry for the (testing noise). I think we are getting close. A check of the dft function for a square pulse, which should give a |
|
It looks like @stggh is very close to a working FH transform. So, probably this isn't especially relevant, but, for the record, I found a matlab implementation of the FH transform hiding in the original BASEX matlab code: https://github.com/PyAbel/PyAbelLegacy/blob/master/BASEX/Matlab/fourier_hankel.m |
|
with 8f6b0bb has this all been solved? I have been away from this for a while, and returned to it for half a day before I went on vacation. What is the current state of play? |
|
I think it would be good (for me at least) to write this up with several analytical tests to make sure it works in various situations. On my own testing, I've found that the normalisation issue we encountered previously in the Gaussian case is due to resolution/finite range. This means the algorithm is correct, but it just needs to be used with care (i.e. it's the user's problem!). It would be good to have a jupyter notebook or something like that to be able to easily run through and see how it's used, where it works and where it doesn't. |
|
Not solved. I left this problem, meaning to come back to it, but I was diverted. Your synopsis is right.
I have spent a lot of time going around in circles due to the spatial/frequency domain issues, and sampling. I am not convinced that your/Baddour like algorithm, without Bessel zero sampling, is correct, but perhaps, I have stuffed the implementation along the way (highly likely). Here are 2 transform pairs that get mangled, the right side is a sampling issue: How would you like to proceed? The hankel-basic.py above has both my version of the Whitaker code and yours, for the sinc transform pair. Is this of any use? |
|
Here is the corresponding jupyter notebook |
|
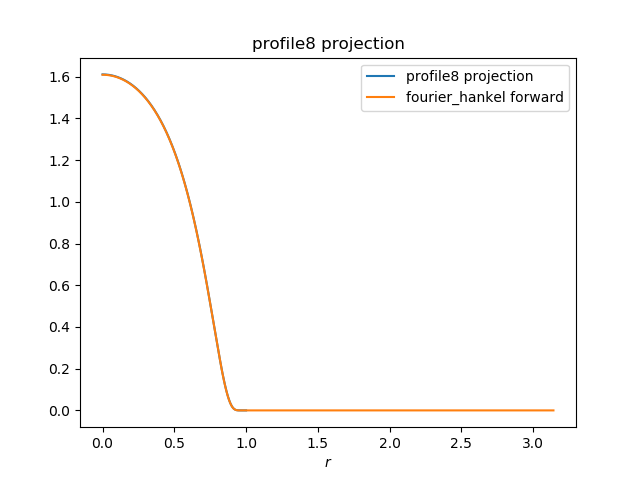
fourier_hankel forward transform appears to be working: The tricky part is the grid corresponds to π r, which may necessitate interpolation to return to the image grid (?). plot code gist using Playing with inverse transform now ... |
|
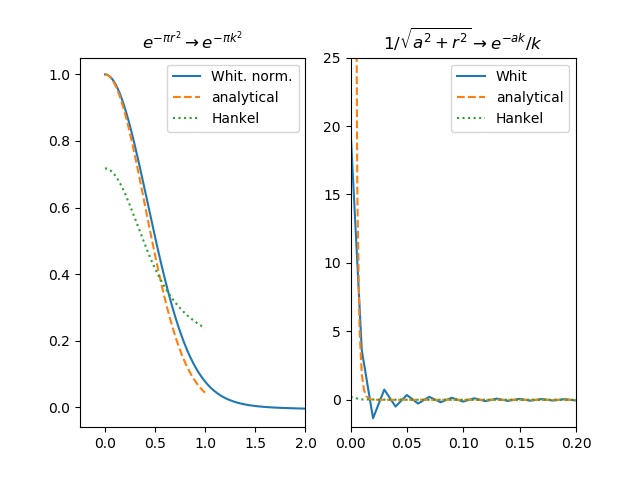
So, no problem with the @steven-murray clever code for the The inverse Abel transform fails: Key code def dht(X, dr=1, nu=0, axis=-1, b=1):
# discrete Hankel transform
N = X.shape[axis]
n = np.arange(N)
freq = n/dr/N
F = b * jn(nu, np.outer(b*n, n/N)) * n
return dr**2 * np.tensordot(X, F, axes=([1], [axis])), freq
def dft(X, dr=1, axis=-1):
# discrete Fourier transform
# Build a slicer to remove last element from flipped array
slc = [slice(None)] * len(X.shape)
slc[axis] = slice(None, -1)
X = np.append(np.flip(X, axis)[slc], X, axis=axis) # make symmetric
fftX = np.abs(np.fft.rfft(X, axis=axis)) * dr
freq = np.fft.rfftfreq(X.shape[axis], d=dr)
return fftX, freq
def fourier_hankel_transform(IM, dr=1, direction='inverse',
basis_dir=None, nu=0, axis=-1):
IM = np.atleast_2d(IM)
if direction == 'inverse':
fftIM, freq = dft(IM, dr=dr, axis=axis) # Fourier transform
# Hankel
transform_IM, freq = dht(fftIM, dr=freq[1]-freq[0], nu=nu, axis=axis)
else:
htIM, freq = dht(IM, dr=dr, nu=nu, axis=axis) # Hankel
transform_IM, freq = dft(htIM, dr=freq[1]-freq[0]) # fft
freq *= 2*np.pi
if transform_IM.shape[0] == 1:
transform_IM = transform_IM[0] # flatten to a vector
return transform_IM, freqNote, this function returns "image" and frequency, unlike the usual I have a feeling that I am missing something obvious for the (Edit: fix code copy error) |
…code of @steven-murray, similar to the algorithm of Baddour JOSAA 32, 611 (2015), doi:10.1364/JOSAA.32.000611, but not evaluated at the Bessel function nodes
|
this looks good! Sorry I haven't had enough time to do anything on this recently. Is there a normalisation problem with the inverse? |
…code of @steven-murray, similar to the algorithm of Baddour JOSAA 32, 611 (2015), doi:10.1364/JOSAA.32.000611, but not evaluated at the Bessel function nodes
|
A good resource with many references on the FHT (or the FFP) is chapter 4 Wavenumber Integration Techniques in Computational Ocean Acoustics (usually available through university accounts). E.g.: chapter 4.5.6. |
|
Hi @gauteh, thanks for pointing this out! When you write FHT, I originally thought that you were referring to the "Fourier Hankel Transform", but now that I have looked up the book chapter, I see that FHT = "Fast Hankel Transform". I believe that @stggh and @steven-murray have some numerical version of the Hankel transform working already. But, probably the references in that book contain more efficient algorithms for the Hankel Transform, which could speed things up. |
|
Danhickstein writes on februar 19, 2018 18:00:
Hi @gauteh, thanks for pointing this out!
When you write FHT, I originally thought that you were referring to the "_Fourier_ Hankel Transform", but now that I have looked up the book chapter, I see that FHT = "_Fast_ Hankel Transform".
I believe that @stggh and @steven-murray have some numerical version of the Hankel transform working already. But, probably the references in that book contain more efficient algorithms for the Hankel Transform, which could speed things up.
Worth checking out at least! I have not looked in detail on the
difference with the implementations here. Both the Fast Field
Approximation and Fast Hankel Transform as described in this reference
use the asymptotic versions of the Hankel functions. But the version of
the Fast Hankel Transform (which does not seem to uniquely refer to one
method) can use the full Bessel functions for lower wavenumbers*ranges
as well as the negative spectrum as well.
|











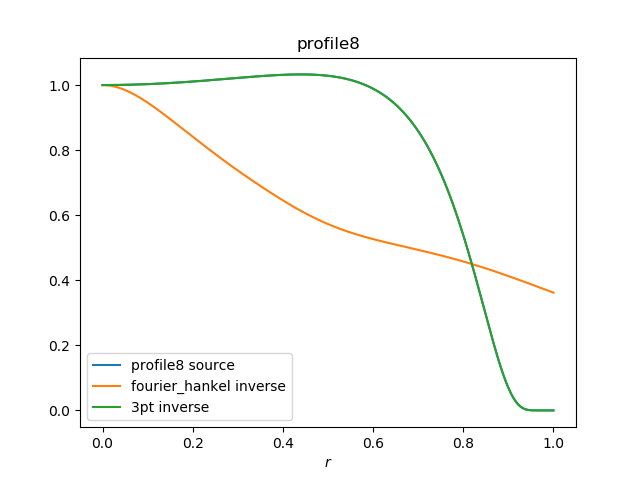
Probably won't be too hard to implement at some point, if somebody is interested. See FHA cycle
The only thing that need to be cheked is whether the Hankel transform can be done exclusively with
numpy,scipy(don't know ifscipy.linalg.hankelis related) or whether we would need to use a separate packagehankel.In which case it can be added as an optional dependency, and this implementation should raise an error if
hankelmodule is not installed (trying to keep the number of additional dependencies low). Or any other way you prefer to handle this.The text was updated successfully, but these errors were encountered: