A python toolbox for simulation of matching markets in economics.
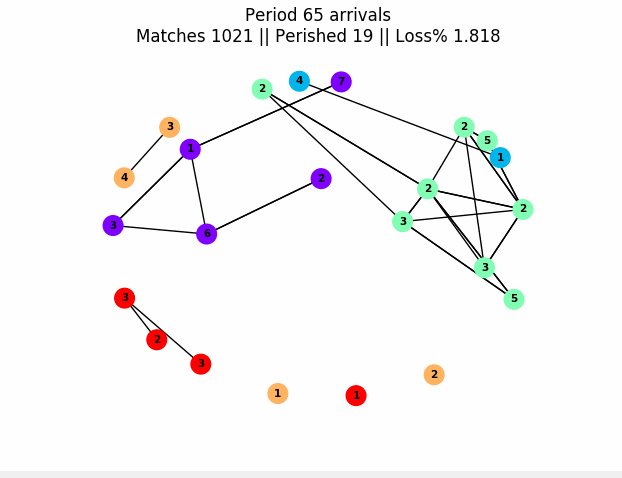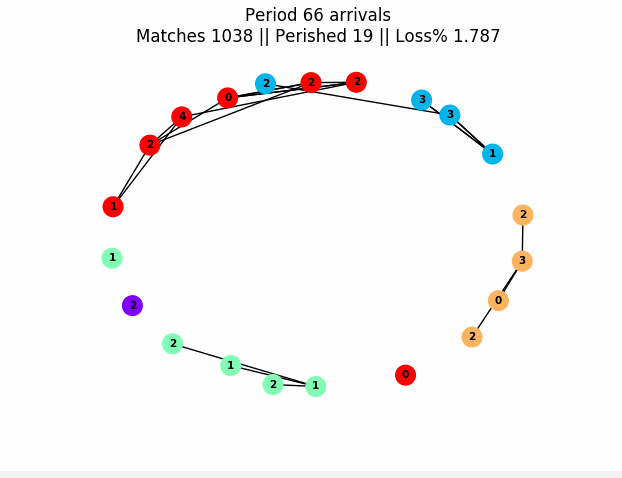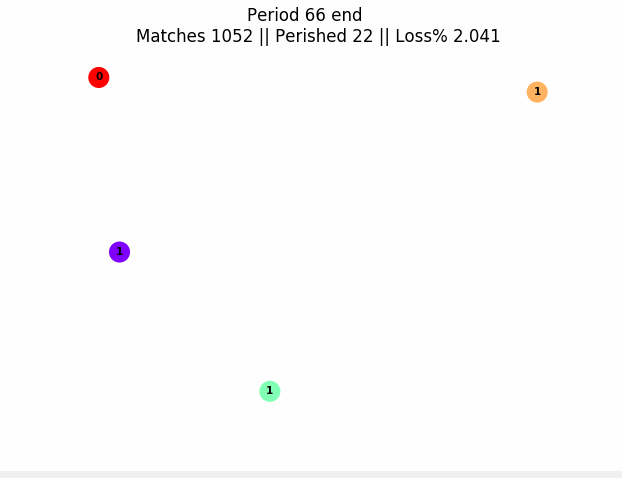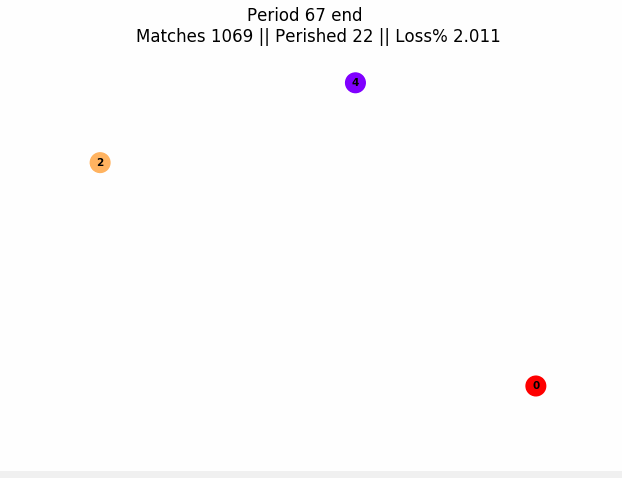
The toolbox uses generic abstractions and python lambdas to produce simulations of general matching markets. Examples of matchings markets are organ exchanges, school/student assignment or matching goods and individuals in a barter economy. These markets can last one period, or can evolve over many time periods. Here is an example of a graph produced with the package of a market evolving over many periods:
In this graph, nodes are people and node color is their "type" (think patient or donor blood type in organ transplants). The number on a node is periods of life left before death if not matched. An edge means they are compatible (it can be weighed if there's risk of failure). Edges get highlighted red before matches. In this simulation, only people of the same type can be compatible, and we naively match two compatible individuals at random. Our timing decision rule here is to naively try to match everyone each period.
The figure can be produced with this code:
import matchingmarkets as mm
import numpy.random as rng
newsim = mm.simulation(time_per_run=100, max_agents=5000,
arrival_rate=15, average_success_prob=lambda: 0.3,
typeGenerator=rng.randint,
compatFct=mm.stochastic_neighborSameType,
crit_input=3, numTypes=5)
# Make sure matplotlib is __not__ inline for this
newsim.graph(plot_time=0.8)
MatchingMarkets.py aims to be "batteries included". If you use the Anaconda distribution with python 3, you should have no problems using the package.
Formally, it requires Python 3.6+, Numpy/scipy, NetworkX, matplotlib with qt5agg backend (for interactive graph plotting) This backend can be changed manually in "Markets.py" A PuLP installation is included by default in matchingmarkets/algorithms/pulp for kidney solvers. This uses the COIN-OR cbc solver by default and can be changed to Gurobi, CPLEX or other compatible solvers manually
-
Random pairwise match (default)
-
Serial dictatorship (serial ordering is user definable with lambda input)
-
Max weight matching (Based on blossom algorithm)
-
Modern kidney solvers are not functional yet.
It can be useful to try out a few settings on generators and visualize the output to see if the simuation is what you want. The current suite of generators is in this file. Currently we have:
-
Random or deterministic assignment of one or multiple abstract types
-
Blood types (for organ transplants)
-
It's easy to write a lambda and pass it in the
typeGeneratorattribute in amm.simulationobject. The lambda should respect the format of generator functions.
More important is the function defining match compatibility based on types of agents. This is in the same file as above. Using abstract types and cutoff values for the RNG, you can simulate many classic matching problems easily. It is also easy to write a lambda which simulates the compatibility you desire as long as it respects the form f(sourceAgent, receivingAgent, cutoff=1) -> float in [0,1] where the result is the match success probability, and cutoff is an optional parameter usually used in an RNG.
Please refer to the tutorial notebook for more in depth instructions.
Download the package, change directory to the one containing it in your python console, and import matchingmarkets as mm.
Intended use is through the simulation object, as follows:
newsim = mm.simulation(
# Simulation parameters here
)
newsim.run()
#prints output of a simulation
newsim.stats()
out[5]:
Simulation Results
1 periods
50 runs
Stat value (std dev)
==================================
Welfare: 50.04 ( 6.7675 )
matches: 50.04 ( 6.7675 )
perished: 0.0 ( 0.0000 )
loss%: 0.0000 ( 0.0000 )
One way to get as much information about your simulation as possible is to run it with the verbose flag on, and plot a few periods:
newsim.verbose = True
newsim.graph(period=10)
# This will print all relevant information to console, and graph the output
The simulation class has many attributes to simulate static (single period) or dynamic (multi-period) matching markets. When creating the simulation class, you can pass the following parameters:
runs: int
number of trials when runs
time_per_run: int
number of time periods in a run
max_agents: int
maximum number of agents over a run overall
logAllData: bool
log every single period on every iteration
Takes much longer, but outputs pretty plots in the stats() function
if false, only logs final results on each run
arrival_rate: int
average number of new agents per period
the lambda in a poisson distribution
average_success_prob: f() -> float[0,1]
cutoff value passed in neighborfct
1 - pr(failure of match) for average of mrkt
algorithm: f(list<agent>) -> dict{agent.name : agent.name}
Matching Algorithm
takes current agents in market as input
returns a list of matches
see algorithms.py for details
arrival_fct: fct(float) -> int
function that returns number of arrival this period
poisson distribution draw by default
crit_input:int
input in time_to_crit, usually param in a rng fct
discount: fct() -> [0,1]
function generating agent discount rate
matchUtilFct: fct(agent1, agent2, float) -> float
returns utility for agent1 of matching to agent2
metaAlgorithm: f(market, algorithm, **kwargs)
-> dict{agent.name : agent.name}
Algorithm responsible for timing decisions
Decides when to match, and who participates
in the matching algorithm
metaParams: dict{string: value}
kwargs passed into the metaAlgorithm
This can then be passed into the Algorithm
neighborFct: fct(agent1, agent2, float) -> float
rng function returning agents who are
compatible matches based on input
float parameter is a cutoff value for rng
numTypes: int
input in typeGenerator
usually # of types
utilityFctInput: float
input for matchUtilFct (usually rng cutoff value)
selfMatch: bool
true if an agent can match himself
ex: House market
false if an agent has to match another
ex: marriage market
time_to_crit: fct() -> int
function generating agent time to crit
typeGenerator: fct(int) -> int
function generating agent type
verbose: bool
print on relevant actions in update
replace plotting animations with Celluloid