New MOLFiniteDifference Discretization

[ChrisRackauckas]

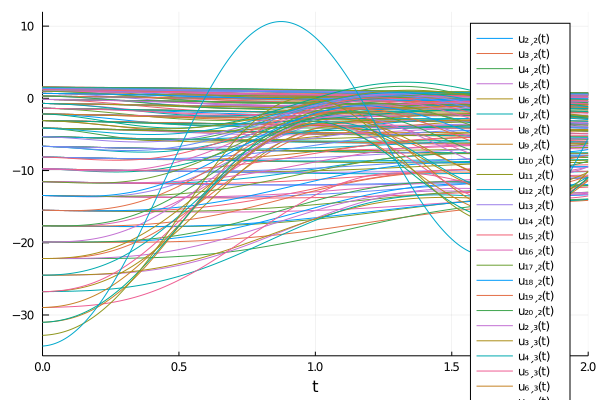
using ModelingToolkit, DiffEqOperators, LinearAlgebra

# 3D PDE
@parameters t x y
@variables u(..)
Dxx = Differential(x)^2
Dyy = Differential(y)^2
Dt = Differential(t)
t_min= 0.
t_max = 2.0
x_min = 0.
x_max = 2.
y_min = 0.
y_max = 2.

# 3D PDE
eq  = Dt(u(t,x,y)) ~ Dxx(u(t,x,y)) + Dyy(u(t,x,y))

analytic_sol_func(t,x,y) = exp(x+y)*cos(x+y+4t)
# Initial and boundary conditions
bcs = [u(t_min,x,y) ~ analytic_sol_func(t_min,x,y),
       u(t,x_min,y) ~ analytic_sol_func(t,x_min,y),
       u(t,x_max,y) ~ analytic_sol_func(t,x_max,y),
       u(t,x,y_min) ~ analytic_sol_func(t,x,y_min),
       u(t,x,y_max) ~ analytic_sol_func(t,x,y_max)]

# Space and time domains
domains = [t ∈ IntervalDomain(t_min,t_max),
           x ∈ IntervalDomain(x_min,x_max),
           y ∈ IntervalDomain(y_min,y_max)]
pdesys = PDESystem([eq],bcs,domains,[t,x,y],[u(t,x,y)])

# Method of lines discretization
dx = 0.1; dy = 0.2
discretization = MOLFiniteDifference([x=>dx,y=>dy],t)
prob = ModelingToolkit.discretize(pdesys,discretization)

using OrdinaryDiffEq
sol = solve(prob,Tsit5())
using Plots
plot(sol)
savefig("plot.png")

[ChrisRackauckas]

[ChrisRackauckas]

using OrdinaryDiffEq, ModelingToolkit, DiffEqOperators
# Method of Manufactured Solutions: exact solution
u_exact = (x,t) -> exp.(-t) * cos.(x)

# Parameters, variables, and derivatives
@parameters t x
@variables u(..)
Dt = Differential(t)
Dxx = Differential(x)^2

# 1D PDE and boundary conditions
eq  = Dt(u(t,x)) ~ Dxx(u(t,x))
bcs = [u(0,x) ~ cos(x),
        u(t,0) ~ exp(-t),
        u(t,1) ~ exp(-t) * cos(1)]

# Space and time domains
domains = [t ∈ IntervalDomain(0.0,1.0),
           x ∈ IntervalDomain(0.0,1.0)]

# PDE system
pdesys = PDESystem(eq,bcs,domains,[t,x],[u(t,x)])

# Method of lines discretization
dx = 0.1
order = 2
discretization = MOLFiniteDifference([x=>dx],t)

# Convert the PDE problem into an ODE problem
prob = discretize(pdesys,discretization)

# Solve ODE problem
using OrdinaryDiffEq
sol = solve(prob,Tsit5(),saveat=0.2)

# Plot results and compare with exact solution
x = (0:dx:1)[2:end-1]
t = sol.t

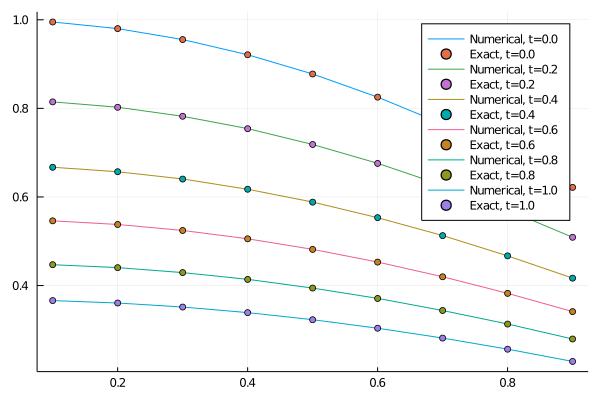
using Plots
plt = plot()

for i in 1:length(t)
    plot!(x,sol.u[i],label="Numerical, t=$(t[i])")
    scatter!(x, u_exact(x, t[i]),label="Exact, t=$(t[i])")
end
display(plt)
savefig("plot.png")

[ChrisRackauckas]

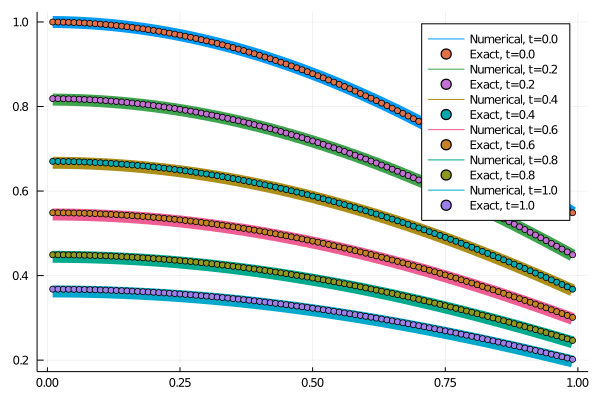
Neumann:

using OrdinaryDiffEq, ModelingToolkit, DiffEqOperators
# Method of Manufactured Solutions: exact solution
u_exact = (x,t) -> exp.(-t) * cos.(x)

# Parameters, variables, and derivatives
@parameters t x
@variables u(..)
Dt = Differential(t)
Dx = Differential(x)
Dxx = Differential(x)^2

# 1D PDE and boundary conditions
eq  = Dt(u(t,x)) ~ Dxx(u(t,x))
bcs = [u(0,x) ~ cos(x),
        Dx(u(t,0)) ~ 0.0,
        Dx(u(t,1)) ~ -exp(-t) * sin(1)]

# Space and time domains
domains = [t ∈ IntervalDomain(0.0,1.0),
        x ∈ IntervalDomain(0.0,1.0)]

# PDE system
pdesys = PDESystem(eq,bcs,domains,[t,x],[u(t,x)])

# Method of lines discretization
# Need a small dx here for accuracy
dx = 0.01
order = 2
discretization = MOLFiniteDifference([x=>dx],t)

# Convert the PDE problem into an ODE problem
prob = discretize(pdesys,discretization)

# Solve ODE problem
using OrdinaryDiffEq
sol = solve(prob,Tsit5(),saveat=0.2)

# Plot results and compare with exact solution
x = (0:dx:1)[2:end-1]
t = sol.t

using Plots
plt = plot()

for i in 1:length(t)
    plot!(x,sol.u[i],label="Numerical, t=$(t[i])",lw=12)
    scatter!(x, u_exact(x, t[i]),label="Exact, t=$(t[i])")
end
display(plt)
savefig("plot.png")

[ChrisRackauckas]

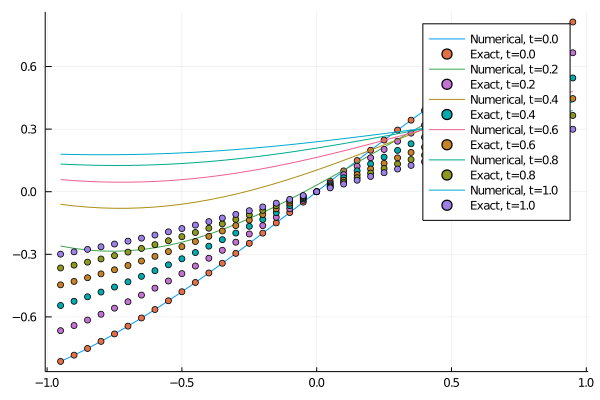
Given the implementation, Robin comes for free, but curiously:

using OrdinaryDiffEq, ModelingToolkit, DiffEqOperators
# Method of Manufactured Solutions
u_exact = (x,t) -> exp.(-t) * sin.(x)

# Parameters, variables, and derivatives
@parameters t x
@variables u(..)
Dt = Differential(t)
Dx = Differential(x)
Dxx = Differential(x)^2

# 1D PDE and boundary conditions
eq  = Dt(u(t,x)) ~ Dxx(u(t,x))
bcs = [u(0,x) ~ sin(x),
        u(t,-1.0) + 3Dx(u(t,-1.0)) ~ exp(-t) * (sin(-1.0) + 3cos(-1.0)),
        u(t,1.0) + Dx(u(t,1.0)) ~ exp(-t) * (sin(1.0) + cos(1.0))]

# Space and time domains
domains = [t ∈ IntervalDomain(0.0,1.0),
        x ∈ IntervalDomain(-1.0,1.0)]

# PDE system
pdesys = PDESystem(eq,bcs,domains,[t,x],[u(t,x)])

# Method of lines discretization
# Need a small dx here for accuracy
dx = 0.05
order = 2
discretization = MOLFiniteDifference([x=>dx],t)

# Convert the PDE problem into an ODE problem
prob = discretize(pdesys,discretization)

# Solve ODE problem
using OrdinaryDiffEq
sol = solve(prob,Tsit5(),saveat=0.2)

# Plot results and compare with exact solution
x = (-1:dx:1)[2:end-1]
t = sol.t

using Plots
plt = plot()

for i in 1:length(t)
    plot!(x,sol.u[i],label="Numerical, t=$(t[i])")
    scatter!(x, u_exact(x, t[i]),label="Exact, t=$(t[i])")
end
display(plt)
savefig("plot.png")

@tinosulzer how sure are you on that Robin BC analytical solution? I would think there's a sign error in there, since the direction of discretization is the same code from the Neumann which works, so I'm not sure what would go wrong if Dirichlet and Neumann work in this implementation.

[ChrisRackauckas]

• Generalize Neumann handling to higher dimensions
• Double check Robin
• Order choice in central
• Higher order derivatives
• Nonlinear Laplacian
• Upwinding
• Remove Overload occursin JuliaSymbolics/SymbolicUtils.jl#251 piracy

[ChrisRackauckas]

Requires JuliaSymbolics/SymbolicUtils.jl#251