王世兴 2013301020050
Problem 4.16 [1]
Carry out a true three-body simulation in which the motions of Earth, Jupiter, and the Sun are all calculated. Since all three bodies are now in motion, it is useful to take the center of mass of the three-body system as the origin, rather than the position of Sun. It is also recommendable to give the Sun an initial velocity to make the total momentum of the system exactly zero (so that the center of mass will remain fixed). Study the motion of Earth with different initial conditions. Also, try increasing the mass of Jupiter to 10, 100, 1000 times of its true mass.
Three-body system is famous for its complexity and an analytical solution is known not to exist. This is where numerical solutions can show its values in scientific significance. A program is accomplished to calculate the motion of Earth, Jupiter, and the Sun under gravitational force. The influence of various initial angle between the position vector from Sun to Earth and from Sun to Jupiter is shown in the figure. Also, the mass of Jupiter is changed with different values to study the chaotic behavior in the three-body problem.
In physics and classical mechanics, the three-body problem is the problem of taking an initial set of data that specifies the positions, masses and velocities of three bodies for some particular point in time and then determining the motions of the three bodies, in accordance with the laws of classical mechanics (Newton's laws of motion and of universal gravitation). [2]
In our problem, the motion of the Sun, Earth, and Jupiter can be describled as
$$\begin{array}{lll}\ddot{r}{Sun}=-\frac{GM{Earth}}{(r_{Sun}-r_{Earth})^3}(\vec{r}{Sun}-\vec{r}{Earth})-\frac{GM_{Jupiter}}{(r_{Sun}-r_{Jupiter})^3}(\vec{r}{Sun}-\vec{r}{Jupiter})\ \ddot{r}{Earth}=-\frac{GM{Sun}}{(r_{Earth}-r_{Sun})^3}(\vec{r}{Earth}-\vec{r}{Sun})-\frac{GM_{Jupiter}}{(r_{Earth}-r_{Earth})^3}(\vec{r}{Earth}-\vec{r}{Jupiter})\ \ddot{r}{Jupiter}=-\frac{GM{Sun}}{(r_{Jupiter}-r_{Sun})^3}(\vec{r}{Jupiter}-\vec{r}{Sun})-\frac{GM_{Earth}}{(r_{Jupiter}-r_{Earth})^3}(\vec{r}{Jupiter}-\vec{r}{Earth})\end{array}$$
-
Initial Position
First we assume that the Sun is at the origin of a coordiante system, and we can figure out the coordinate of the center of mass. Then by subtracting this position vector from all position vectors of the three bodies can we yield the coordinates in the center-of-mass coordinate system. -
Initial Velocity
It is advised to choose the center of mass of the three bodies as the origin of the coordinate system, while making the total momentum of the system zero so that the center of mass remain at a fixed point. Since the trajectories of the three bodies are restrained in a plain, there are only six degrees of freedom in the system. The center of mass remaining at the origin gives us one vector equation, and the speed of circular motion under gravitational force gives us two vector equations, making the initial conditions dependent only on the angle .
$$\begin{array}{ll}|\vec{v}{Earth}-\vec{v}{Sun}|=\sqrt{GM_{Sun}}\sqrt{\frac{1}{r_{ES}}(1+\frac{M_{Earth}}{M_{Sun}})}\|\vec{v}{Jupiter}-\vec{v}{Sun}|=\sqrt{GM_{Sun}}\sqrt{\frac{1}{r_{JS}}(1+\frac{M_{Jupiter}}{M_{Sun}})}\end{array}\\vec{v}{Sun}=-\frac{M{Earth}}{M_{Sun}}\vec{v}{Earth}-\frac{M{Jupiter}}{M_{Sun}}\vec{v}_{Jupiter}$$
With Wolfram Mathematica, we get the initial velocities:
Notice that the solutions are ontained under the assumption that the force from the planets are negligible. While this is not the case when the mass of Jupiter is appreciable, the results when Mj is very large may not be that convincing.
We tried four representative angles between the positon vector from Sun to Earth and from Sun to Jupiter. Since at the true mass of Jupiter we can naturally imagine that the result would not be sensitive to initial conditions. We changed the mass of jupiter to 100 times of its true value. We can see when the three bodies are in a line, Earth will still remain between the Sun and jupiter, while a different angle would "kick" Jupiter off.
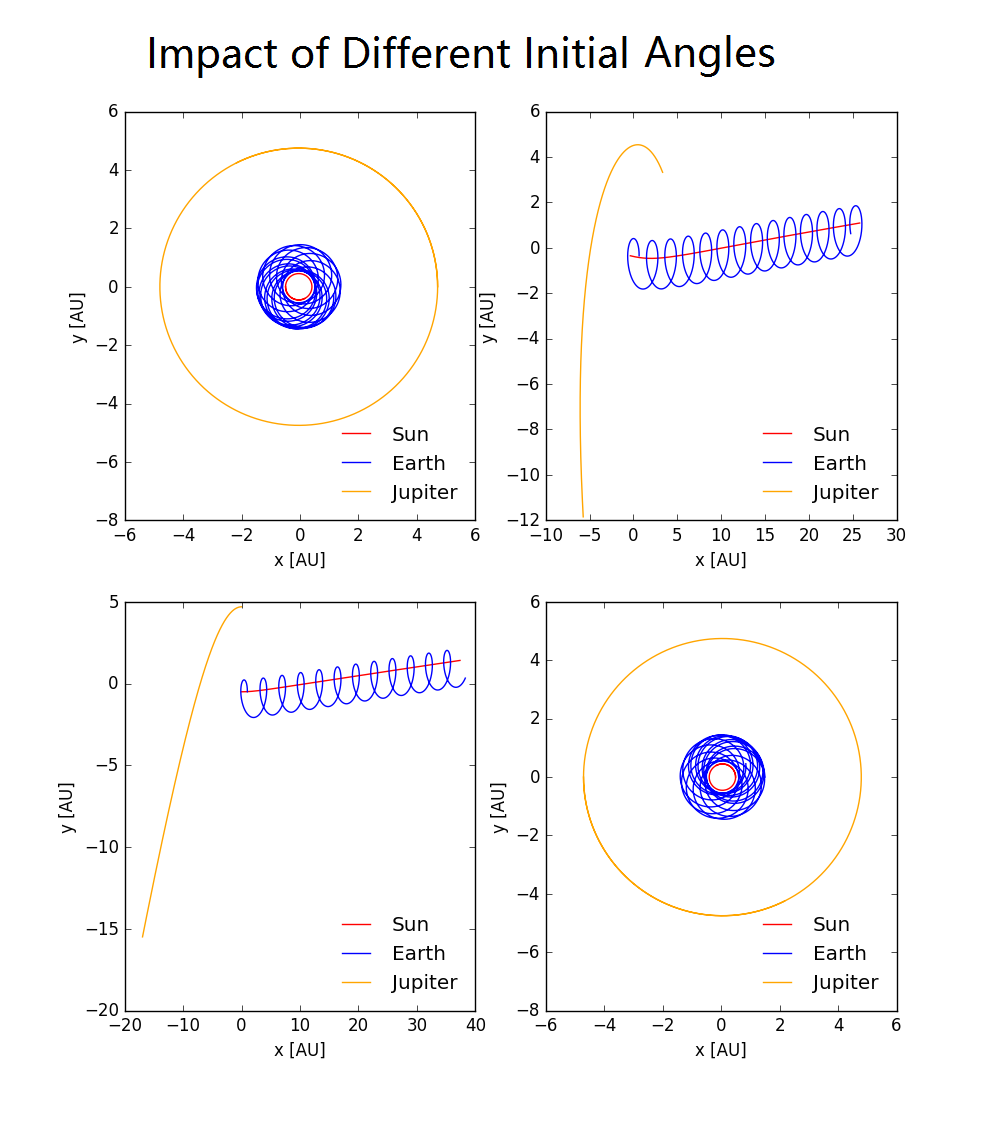
Figure 12.1 Three-body simulation with different initial angle between the positon vector from Sun to Earth and from Sun to Jupiter. Simulated time is 15 years and time step is 0.0001 year. The angle
The figure below shows the impact of different mass of Jupiter. When simulating with true mass of Jupiter, the system behaves just like what the solar system nowadays is. When the mass of Jupiter becomes ten times its true mass, the trajectory of Earth is perturbed, like a bold ring. The 100-time mass makes the trajectory much more drastic with its radius changing from a large range. when Jupiter is 1000 times the same mass as its true mass, it would be comparable with Sun, the two big body would spin around an axis between them and the earth would go around one of them, or even be caught by the other under certain occassions.
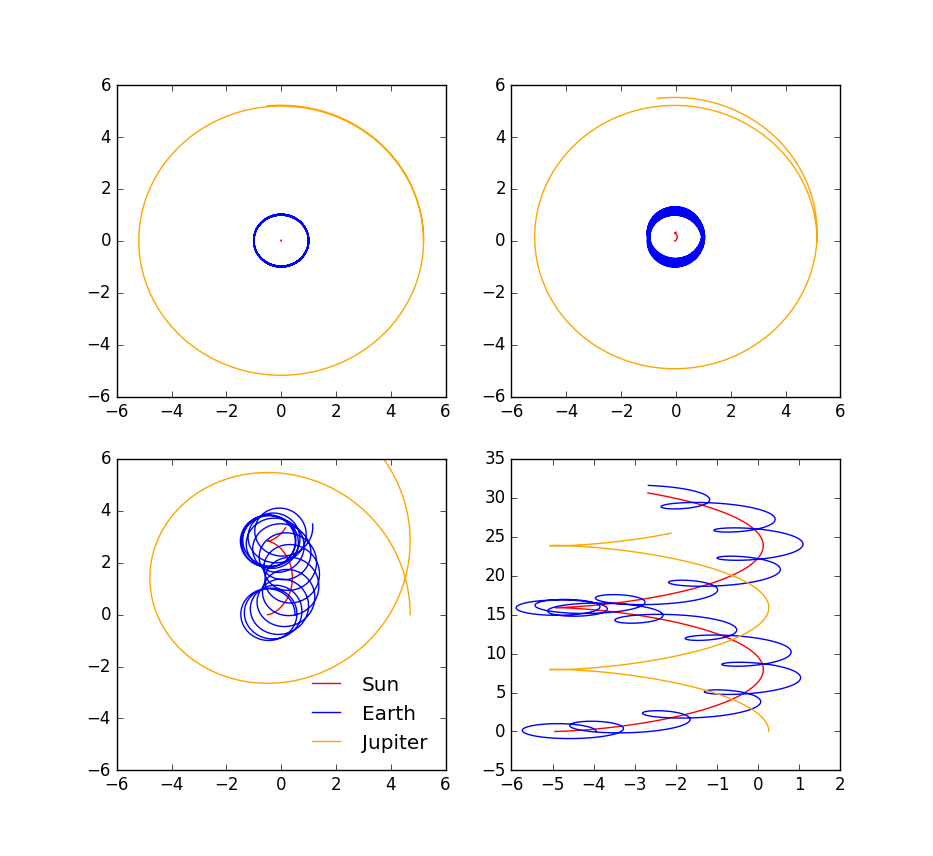
Figure 12.2 Three-body simulation with various values of the mass of Jupiter. Simulated time is 10 years and time step is 0.0001 year. The "Jupiter" mass is the same (upper left), 10 times (upper right), 100 times (lower left) and 1000 times (lower right) as the real mass of Jupiter, respectively.
-
Giodano, N.J., Nakanishi, H. Computational Physics. Tsinghua University Press, December 2007
-
Three-body problem. (2016, May 14). In Wikipedia, The Free Encyclopedia. Retrieved 04:11, May 15, 2016, from https://en.wikipedia.org/w/index.php?title=Three-body_problem&oldid=720180887