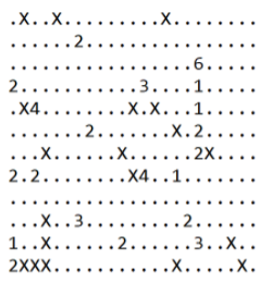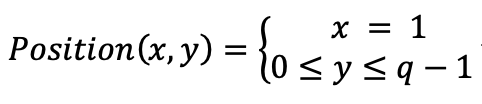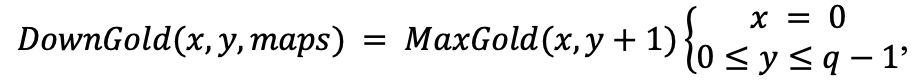COSC2658 Data Structures and Algorithms - Group Project

Team 24:

• Ngo Nguyen Tien Dat - s3804687
• Le Nguyen Minh Huy - s3777280
• Nguyen Pham Quoc Minh - s3812649
• Nguyen Thanh Thien - s3817852

I. Problem description

The group assignment in COSC2658 course requires our group to implement two different algorithms with different strategies in the Java programming language to solve Greedy Gnomes Problem. Specifically, our Mr Gnome will traverse through the mine area, represented under a matrix with a maximum of twenty-seven (27) rows and columns, as indicated in the figure below.

Given the matrix, Mr. Gnome needs to find the path, including the number of steps, from the starting point (X-axis at 0, Y-axis at 0) in which he will maximize his total amount of gold collected while avoiding obstacles like rocks (the "X" symbol) on the way. However, due to the constraint of the challenge, heading towards the down or right direction upon each step are the only viable options. On the other hand, many optimal paths could co-exist in one mine area; thus, picking one of the optimal paths is the only required solution to this particular problem.

II. Approach

1. Exhaustive Search

1.1 Algorithm description

The Exhaustive Search approach is the first proposed algorithm that aims to search for the optimal path with the most collected gold on the given mine area. The algorithm's underlying mechanism obviously remains exhaustive, which means that the accumulation of gold collected is calculated for every valid path on the matrix and then compared with others to find the maximum number. Upon obtaining the maximum, the path's directions, down or right, are also being tracked on every possible state generated. Concretely, a backtracking technique that checks all possibilities and verifies whether the requirements are obtained is ideally used to find the optimal result among a set of all feasible solutions. Besides, the team has also defined a safe path is when it satisfies the boundary conditions, which means the current position's row and column coordinate are greater than or equal to zero (0) and less than the number of rows and columns of the matrix, and the current position of that path must not be a rock as well.

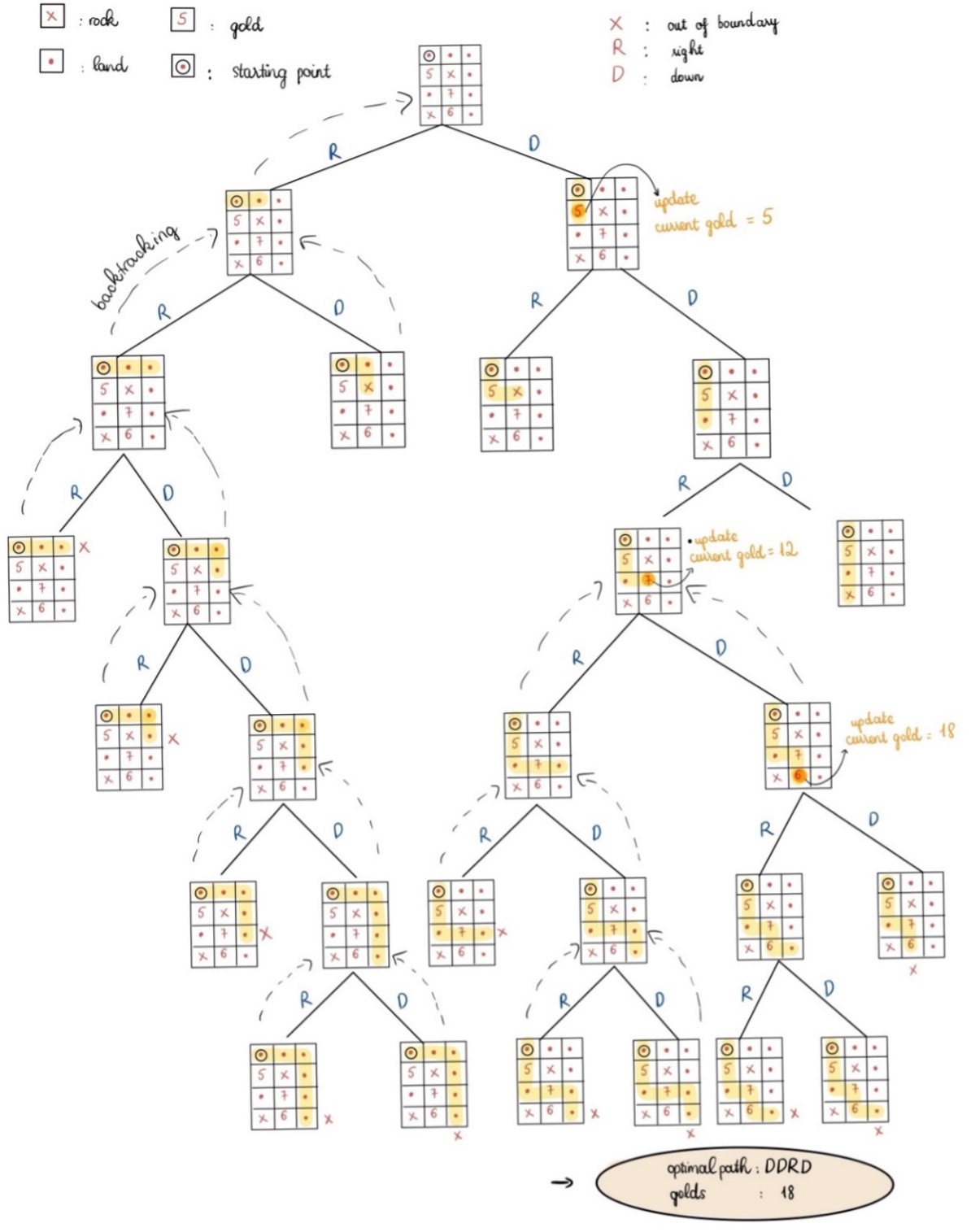
To deeply understand how the algorithm works, the team has visualized the process of running the exhaustive search algorithm in detail (Figure 2). According to the statement of the problem, there are two way to traverse, that are going right (R) or going down (D). The algorithm starts at the point having coordinate of (0,0) then traverses vertically (D) and horizontally (R) until it cannot possibly complete the conditions for a valid path. Intuitively, each state has two options in term of directions, whenever it reaches any of the boundary edges of the matrix or a rock, the backtracking technique will be applied to abandon that partial candidate and continue to find the optimal solution. To be more specific, looking at the figure 2, when the path is RRR, it is obviously that we cannot expand the path to the right; hence, it goes back to the previous state and traverses in a down direction. On the other hand, when reaching gold, the score is cumulatively added to the current gold variable. With a simultaneous, the team also compares the current score with the final score variable and update the final one if the current score is greater than. By doing that, the team can keep track the path's Direction as well as the steps and the number of gold pieces on every state.

1.2 Pseudo code

// Class for constructing solution object
// including the gold, path of the optimal solution and total steps of the path
CLASS Solution IS
	int gold;
	String path;
	int steps;

// Scout the mine area to perform calculations and comparisons
// on every valid path
FUNCTION scout(x, y, matrix, solution, currentGold, currentDirection, currentPath)
IF  (x < 0 OR y < 0 OR x >= matrix’s rows OR y >= matrix’s columns OR matrix[x][y]       == -1)
		RETURN // Stop scouting & Do nothing
IF (currentDirection is not null)
		UPDATE currentPath by appending the currentDirection
	// Check if current coordinate has any gold
IF (matrix[x][y] > 0)
		INCREMENT currentGold by the amount of gold in the coordinate
// Compare to obtain the maximum/optimal one
IF (currentGold > solution.gold)
		SET solution.gold as currentGold
		SET solution.steps as the length of currentPath
		SET solution.path as currentPath
	// Recursively scout for other directions from the current path
CALL scout(x + 1, y, matrix, solution, currentGold, "DOWN", currentPath)
CALL scout(x, y + 1, matrix, solution, currentGold, "RIGHT", currentPath)
// Backtrack the visited path
IF (length of currentPath > 0)
		UPDATE currentPath by deleting the latest traversed direction	

// -- Main program to solve the problem -- //
// Parse integer-based matrix from file
matrix = parseIntFromFile(file)
solution = new Solution()
currentPath = ""
scout(0, 0, matrix, solution, 0, null, currentPath)
// Display results
PRINT solution.gold // Maximum gold collected
PRINT solution.steps // Total steps of the optimal path
PRINT solution.path // String of directions for the optimal path

1.3 Complexity analysis

The time complexity of the function in the worst possible case, in which no obstacles (rocks) are found in the matrix, could be computed as the following formula: T(m + n) = T(m – 1 + n) + T(m + n – 1) + c*T(1)

To clarify the above function, c is the constant for independent operations.

The formula can be simplified to: T(m + n) = 2T(m – 1 + n) + cT(1)

Since the recursive child function once again calls itself twice with different arguments, the equation below indicates the time for the recursion:

T(m – 1 + n) = T(m – 1 – 1 + n) + T(m – 1 + n -1) + c*T(1)

Thus, the Big-O complexity of the scout function can be reduced to the exponential of base two. Moreover, with leading-term approximations, the team has ignored the constant coefficient in lower-order. Therefore, the final time complexity of scout function is:

T(m + n) = O(2^(m+n))

2. Dynamic Programming

2.1 Algorithm description

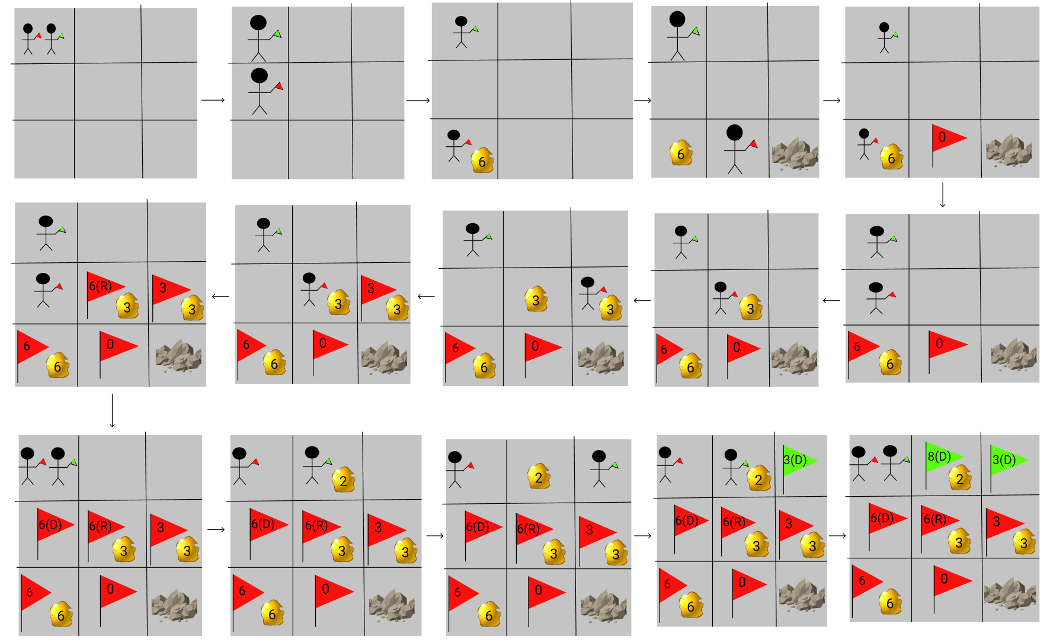
With respect to Dynamic Programing Top-Down approach, our team has visualized the process step by step through figure 3. Imaging there are two people who are gold diggers, both can move down and right direction. Specifically, person 1 who is holding red flat will start the journey and he must move down direction first; for person 2 who is holding green flat goes in right direction. At each point, 2 gold diggers can scout the next right or down point for discovering rocks or edges as well as discover how many golds at their standing positions. If there is no available way to go, the gold digger marks the position by the flat as well as note down how many pieces of gold they have found so far on these flats, then gradually go back to the starting position. After person 1 has finished the trip, person 2 can start and if there is a red flat, person 2 will not need to go the direction that has the flat anymore. Similarly with person 1, if there is no available way to go, person 2 will go back to the beginning position and on the way, person 2 will mark the position and count collected gold.

2.2 Pseudo code

// Class for constructing solution object
// including the gold, path of the optimal solution and total steps of the path
CLASS Solution IS
int gold;
String path;
int steps;

// Unit class to store data from previous travel of the algorithm, the class contain these information
// goldLeft: the total amount of the maximum goal that the agent can collect from the respective sign
// Direction: the next Direction to follow the optimized path
CLASS Sign IS
int goldLeft;
Direction direction; // DOWN or RIGHT 
// Main Program
// Input data is a matrix of integer having size of [m,n], where m stand for number
// row and n stand for number of columns
// First we construct a map containing units of class sign to save information when 
// the algorithm travel through the map 
Signs = Sign[m][n]
// Then we use DPscout function to update Signs
// The function using these input: 
// - x,y is the coordinates of the current position of the map 
// Matrix is the integer matrix store values of the map where 0 stands for  
FUNCTION DPscout(x,y,direction,Matrix,Signs):
// case 1: when the current position is having all path blocked 
 	IF (Matrix[x][y] == -1)
    return 0
// case 2: when the current position is out of the matrix shape
IF (x > Matrix’s Number of Row || y > Matrix’s Number of Columns)
    return 0
// case 3: when the algorithm traveled the current position
IF (signs[x][y] != NULL)
    return signs.goldLeft
// calculate the normal case when the position is not visited and not blocked
DownGold = scout(x + 1, y, DOWN, Matrix, signs)
RightGold = scout(x, y+1, RIGHT, Matrix, signs)
CurrentGold = Matrix[x][y]
TotalGold = CurrentGold
// checking conditions for update signs
IF (DownGold > RightGold) 
TotalGold += DownGold
Signs[x][y] = new Sign(TotalGold, RIGHT)
ELSE IF (RightGold> DownGold) 
TotalGold += RightGold
Signs[x][y] = new Sign(TotalGold, DOWN)
// If EQUAL, calculate total gold with DOWN or RIGHT (optional) direction
// Here we choose DOWN as an option
totalGold += DownGold
// Skip initializing sign if totalGold is equal to Zero
IF (totalGold == 0)
    RETURN 0
// If both directions return 0 gold, initializing sign without upcoming direction
IF (DownGold = RightGold == 0)
    Signs[x][y] = new Sign(TotalGold, Null)
    RETURN TotalGold
// Initializing signs
Signs[x][y] = new Sign(TotalGold, Direction.DOWN);
RETURN TotalGold

2.3 Complexity analysis

RightGold Calculation: Since this calculation mean that the function will be called to calculate for points at location

which mean that they will located within the calculated map(p,q) so the total RightGold calculation will be q×b

DownGold Calculation: The DownGold Calculation will result in a list of dependent calculation presented by this equation:

, which mean that the first operation need to be completed will be the equations at Position(1,q-1) which has its DownGold calculation is the Scout function alled on an invalid map position, resulted in the b operation cost for that specific coordinate. After we saved the results of the bottom map position and begin to trackback, everytime the DownGold calculation will called the function on a computed cell, which resulted in the cost of b for each case. Therefore the total operation cost for DownGold is q×b.

Combined them together: T(p+1,q)=(a+2b)×p×q+a×q+b×q+b×q

Which mean: T(p+1,q)=(a+2b)×q×(p+1)

So that the time complexity of the horizontal extension case obey the initial rules, which conflict which the assumption ( What need to be proof) Therefore, T(m,n) = C×m×n or O(m,n) = m×n.

III. Conclusion

By implementing two algorithms which are exhaustive search and dynamic programming, the team has solved the Greedy Gnomes problem and achieve the optimal result as expected. Although the problem could be accomplished through many different approaches, thinking of brute-force concept which is well known as a straightforward method and trying all possibilities at the beginning stage makes our team really understand the statement of the problem without concerning about efficiency. The team has proposed 2 algorithms and illustrated the process step by step via visualization as well as proved and analysed the time complexity both of them. Furthermore, experimental running the algorithm on a specific computer also conducted and described through graph and empirical analysis. Knowing the order of growth of algorithm’s running time is one of the most crucial requirements since it provides accurate information about the limitations on the input size of the given problem and helps our team calculate the execution time accordingly.