GSoC 2021 Projects
equadratures is an open-source library for uncertainty quantification, optimisation, numerical integration and dimension reduction–--all using orthogonal polynomials. It is particularly useful for models / problems where output quantities of interest are smooth and continuous; to this extent it has found widespread applications in computational engineering models (finite elements, computational fluid dynamics, etc).
We advise new contributors to first have a look through some of the equadratures tutorials in order to familiarise themselves with the code and some common use cases. More advanced applications can also be found in the Blog and Publications categories on our discourse.
If you are interested in applying to GSoC with equadratures, please do get in touch on the GSoC 2021 discourse post, where we'll be happy to discuss project ideas further and give tips on possible beginner friendly PR's to tackle.
- Enhancing the user experience
- The universal quadrature repository
- Performance optimisation
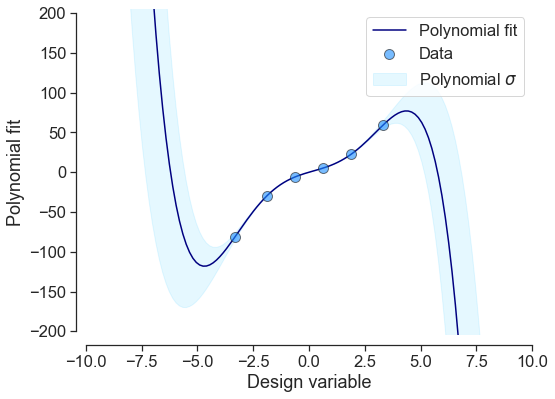
equadratures is seeing increasing applications across academia and industry. As part of an ongoing effort to make the code more approachable to a wider audience, this project will involve enhancing the user experience in three ways. Visualising various equadratures objects, and their underlying data, is a crucial task in many equadratures use cases. To reduce the amount of boilerplate code required for visualisations we have started developing in-built plotting methods, a few examples are shown below.
This project would involve enhancing this capability, which would include expanding the range of plotting methods and improving user customisation. Updating our tutorials to show off this new user-friendly capability would also be an important part of the project. This would provide the student a fundamental understanding of some of the key building blocks within the code. Depending on the students interests, there is also the possibility of constructing an interactive set of tutorials using streamlit, which we would embed within our equadratures.org site.
- Development of visualisation methods/functions for the main equadratures classes, including
Parameter,Basis,Poly,SubspacesandPolyTree. These include (i) pie / bar charts for Sobol' indices; (ii) zonotope plots with response surfaces; (iii) polynomial response surfaces with points. - Integration of the new visualisation capability into the existing tutorials, and development of new tutorials where necessary (note that code for most of the tutorials is already avaliable). Additionally, for tutorials that cover some of the underlying mathematics, it would be useful to have a slides plugin.
- Development of an interactive streamlit app which will allow users to explore key functionality and use cases of equadratures.
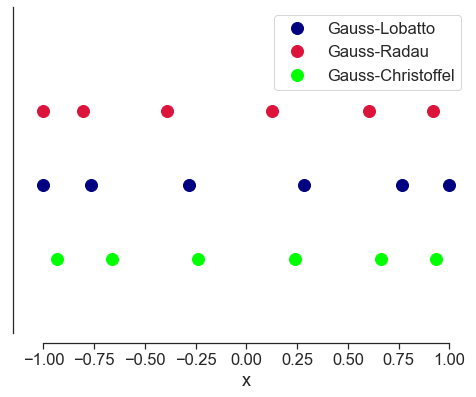
Delivering accurate quadrature rules---for numerical integration---remains one of the key tenets of equadratures. While there has been much research, particularly into high-dimensional numerical integration, no universal repository of such quadrature rules exists. In this project, we wish to lay the foundations for such a universal repository of numerical integration rules. The scope of this project will be limited to integration over a hypercube, e.g., line in 1D; square in 2D; cube in 3D, you get the idea.
This brings us to the main deliverables of this project:
- Validation of existing Gauss-Radau and Gauss-Lobatto quadrature rules (in
parameter.pyand their use inpoly.py), under different distributions, and a tutorial on them. For multivariate problems understanding the degree of exactness offered when combining them through sparse and tensor product grids. - Development of Gauss-Turan quadrature rules (with second derivatives), its testing (creating a test function
test_numerical_integration.py) and a tutorial on it. - Addressing the limitation in the Golub-Welsch algorithm for Gaussian quadrature (see this). Note that this deliverable will require a good background in numerical linear algebra and optimisation.
One of the central tenets of classical machine learning is the bias-variance tradeoff, which implies that an accurate model must balance under-fitting and over-fitting. In other words, it must be rich enough to express underlying structure in the training data, but simple enough to avoid over-fitting to spurious patterns in the data. However, in modern machine learning practice, very complex models (such as deep neural networks) are trained to exactly fit the training data. Such models are technically over-fit, yet in practice, they often obtain high accuracy on test data. This apparent contradiction is caused by double descent [1], a striking phenomenon whereby increasing the model complexity (or decreasing the amount of training data!) beyond a certain point can result in the test error decreasing once again.

Recently, this phenomenon has seen increasing attention in the machine learning community, since it has important implications for how we build models which can generalise to test data effectively. It is desirable to avoid the double descent behavior, and have test error decrease monotonically with increased model complexity and/or increased amounts of training data. One way to achieve this is by adding regularisation, which if optimally tuned can mitigate double descent in many learning algorithms, from neural networks to linear regression [2]. equadratures has a elastic-net regularisation option, where and
penalty terms are added to the loss function:

The strength of the regularisation is controlled by the parameter. We need to be able to find the optimal
value for a given dataset and polynomial. In equadratures we do this by solving the elastic-net via coordinate descent [3], which gives us the full regularisation path (i.e. the solutions for the full range of
values, see below!), so that the optimal
value can be chosen.

The elastic-net sovler in equadratures has worked well on the problems it has been tested on, but it's still a work in progress. It is an iterative solver, but is currently written in pure Python/NumPy, meaning its slower than it could be. This project will first involve properly testing and understanding the solver in equadratures, with a key focus being to ascertain the benefits of using regularisation within the code. The second major part of the project will be to explore how the solver can be optimised with regard to speed. This may involve simply reworking sections of the solver, but is more likey to involve rewriting the solver in a compiled language (e.g. using cython or f2py. Optimising the solver's performance would allow users to tackle larger real-world machine learning datasets.
- Validate and benchmark the elastic-net solver within the
developbranch of equadratures. Properly understanding the effect of this regularisation on orthogonal polynomials, and how it behaves in the context of the double descent phenomenon, will be an important contribution. - Profile the solver using cProfile or another profiling library, in order to help formulate an optimisation strategy.
- Optimise the solver to be able to quickly obtain regularisation paths on large datasets. This is likely to involve rewriting the solver in a compiled language. We are flexible on the choice of C/C++ or Fortran based tools (e.g. cython or f2py) here, and it may come down to the student's previous experience.
[1]: Belkin, M. et al. (2019). Reconciling modern machine-learning practice and the classical bias–variance trade-off. Proceedings of the National Academy of Sciences, 116 (32) 15849-15854; DOI: 10.1073/pnas.1903070116. Paper. arXiv:1812.11118.
[2]: Nakkiran, P. et al. (2020). Optimal Regularization Can Mitigate Double Descent. arXiv:2003.01897.
[3]: Friedman, J. et al. (2010). Regularization Paths for Generalized Linear Models via Coordinate Descent. Journal of Statistical Software, 33(1); DOI: 10.18637/jss.v033.i01. Paper.