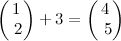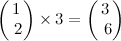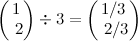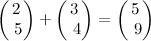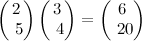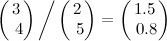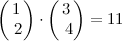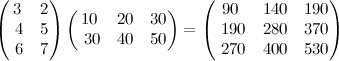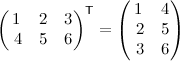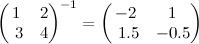This note provides a concise tutorial on how you may use Apple's Accelerate framework with the Swift programming language to perform vector/matrix manipulations, including matrix transposes, dot products, matrix inversions, etc. A playground illustrating all the functions discussed here is included. Also, a better formatted version can be accessed at here.
- Select your project by clicking on the blue icon in the top left corner.
- In the
TARGETSlist (the panel in the middle), select the target you're compiling and then activate theBuild Phasestab. - Click on the little triangle in front of
Link Binary With Libraries. - Click on the
+sign and selectAccelerate.frameworkin the popup.
Now that your project is linked against Accelerate, you can import it in your .swift file by issuing:
import Accelerate
The general syntax for adding a scalar to a vector and for multiplying or dividing a vector by a scalar is as follows
vDSP_vs***D(vector, 1, &scalar, &result, 1, length_of_vector)
The 1s tells the function to operate on each element of the vector. If you replace 1 with 2, it'll operate on every other element instead. Needless to say, for most LA applications, you'll be sticking with 1, as we do for the rest of the tutorial. A few example should make everything crystal clear:
var v = [1.0, 2.0]
var s = 3.0
var vsresult = [Double](count : v.count, repeatedValue : 0.0)
vDSP_vsaddD(v, 1, &s, &vsresult, 1, vDSP_Length(v.count))
vsresult // returns [4.0, 5.0]vDSP_vsmulD(v, 1, &s, &vsresult, 1, vDSP_Length(v.count))
vsresult // returns [3.0, 6.0]vDSP_vsdivD(v, 1, &s, &vsresult, 1, vDSP_Length(v.count))
vsresult // returns [0.333333333333333, 0.666666666666667]Vector-vector operations pose no challenge to Accelerate and the associated functions look like
vDSP_v***D(vector_1, 1, vector_2, 1, &result, 1, length_of_vector)
Here are a few worked-out examples:
var v1 = [2.0, 5.0]
var v2 = [3.0, 4.0]
var vvresult = [Double](count : 2, repeatedValue : 0.0)
vDSP_vaddD(v1, 1, v2, 1, &vvresult, 1, vDSP_Length(v1.count))
vvresult // returns [5.0, 9.0]vDSP_vmulD(v1, 1, v2, 1, &vvresult, 1, vDSP_Length(v1.count))
vvresult // returns [6.0, 20.0]vDSP_vdivD(v1, 1, v2, 1, &vvresult, 1, vDSP_Length(v1.count))
vvresult // returns [1.5, 0.8]var v3 = [1.0, 2.0]
var v4 = [3.0, 4.0]
var dpresult = 0.0
vDSP_dotprD(v3, 1, v4, 1, &dpresult, vDSP_Length(v3.count))
dpresult // returns 11.0Matrices are passed into Accelerate as 1D arrays. As a result, matrix addition/subtraction is the same as vector addition/subtraction.
Matrix multiplication, on the other hand, is a bit more involved and requires this function:
vDSP_mmulD(matrix_1, 1, matrix_2, 1, &result, 1,
rows_of_matrix_1, columns_of_matrix_2,
columns_of_matrix_1_or_rows_of_matrix_2)For example,
var m1 = [ 3.0, 2.0, 4.0, 5.0, 6.0, 7.0 ]
var m2 = [ 10.0, 20.0, 30.0, 30.0, 40.0, 50.0]
var mresult = [Double](count : 9, repeatedValue : 0.0)
vDSP_mmulD(m1, 1, m2, 1, &mresult, 1, 3, 3, 2)
mresult // returns [90.0, 140.0, 190.0, 280.0, 370.0, 270.0, 400.0, 530.0]Matrix transpose can be obtained with
vDSP_mtransD(matrix, 1, &result, 1, number_of_rows_of_result, number_of_columns_of_result) Like this,
var t = [1.0, 2.0, 3.0, 4.0, 5.0, 6.0]
var mtresult = [Double](count : t.count, repeatedValue : 0.0)
vDSP_mtransD(t, 1, &mtresult, 1, 3, 2)
mtresult // returns [1.0, 4.0, 2.0, 5.0, 3.0, 6.0]Matrix inversion takes a bit more effort, but can be accomplished with the function below (see Stack Overflow):
func invert(matrix : [Double]) -> [Double] {
var inMatrix = matrix
var pivot : __CLPK_integer = 0
var workspace = 0.0
var error : __CLPK_integer = 0
var N = __CLPK_integer(sqrt(Double(matrix.count)))
dgetrf_(&N, &N, &inMatrix, &N, &pivot, &error)
if error != 0 {
return inMatrix
}
dgetri_(&N, &inMatrix, &N, &pivot, &workspace, &N, &error)
return inMatrix
}
var m = [1.0, 2.0, 3.0, 4.0]
invert(m) // returns [-2.0, 1.0, 1.5, -0.5]