Data Structures And Algorithms

Problem condition

Solve the problem of graph theory:
"Find the length of the longest simple path from city A to city B in a given system of one-way roads."

Initial problem data

• S is a road system, S = {(name_1[i], name_2[i], weight[i]) | name_1[i], name_2[i] ∈ <сity>, weight[i] ∈ R+, i ∈ N}
• <сity> ::= {g[j] | g[j] ∈ {subset of Russian and Latin letters} ∪ N, j ∈ N}
• name_1[i] is the city specifying the beginning of the road
• name_2[i] is the city specifying the end of the road
• weight[i] is the length of the road between cities name_1[i] and name_2[i]

Result

• max ∈ R+
• Road = {a[i] | a[i] ∈ <city>, i > 1, i ∈ N} || {the message that the desired road does not exist}

External representation of the one-way road system

• An example of the input file and the results of the program for this road system are added to the project.
• The departure city is on the first line of the input file.
• Destination city is on the second line.
• All possible routes between cities are indicated after.

<road system> ::= <departure city> {new line} <destination city> {new line} <road list>
<departure city> ::= <city>
<destination city> ::= <city>
<road list> ::= <road> {new line} <road list> | {empty}
<road> ::= <from> {space} <whereto> {space} <road length>
<from> ::= <city>
<whereto> ::= <city>
<city> ∈ R+
<city> ::= {character sequence} | {number}

Input file example:

• In the external view of the road system, isolated cities are not displayed.
• Also in the input file we will not specify the number of cities in the road system. It will allow you not to make restrictions on the number of cities in the road system, as well as make it easier for the user to enter the input data. First, there will be no need to count the number of cities before entering the road system, and if you change the road system, there will be no need to recalculate it. Second, the amount of data needed to get a result will be reduced.

Internal representation of the road system

• Since in this problem we work with a system of roads, in most cases the graph will be sparse, i.e. the set of edges will be much smaller than the set of vertices. So the adjacency matrix and incident matrix of the graph will consist mostly of zeros, which leads to unnecessary waste of memory.
• The inconvenience of the list of graph edges is the large number of steps needed to get the set of vertices to which the edges lead from the given vertex.
• So we represent the original road system by its adjacency list, since it gives a compact representation for sparse graphs.
• In order not to complicate the lists of adjacency we mark the vertex by a number instead of the name of the city. The vertices of the graph will be numbered starting from zero.
• List of adjacent vertices shall be a linear one-way list. This will not impose restrictions on the number of roads from each city.
• City names will be represented by a vector of strings, and the adjacency list of the graph by a vector of structures, which allows to make no restriction on the number of cities in the road system.

– adjacency structure (lists of adjacent vertices of the graph):

struct wtable
{
   int top;
   double weight;
   wtable *next;
};
vector wmas;

– list of city names:

vector cities;

External output representation

max ∈ R+, which is the length of the longest simple path || {the message that the desired road does not exist}
Road = <sequence of cities>
<city sequence> ::= <city> {space} {"—"} {space} <city sequence> | <city> {space} {"—"} {space} <city>

Mathematical model

• The mathematical model of a one-way road system is an oriented, weighted, labeled, cyclic, not necessarily connected, multi- and pseudograph G = (V, E) with weight function w: E → R, where w(u, v) ≥ 0 for all (u, v) ∈ E.
• To solve problem, it is not necessary to keep loops, roads to the departure city, roads from the destination city, and from multiples only the longest road needs to be kept. On this basis, the mathematical model of this one-way road system can be simplified, so that the mathematical model is a oriented, weighted, labeled, cyclic, not necessarily connected graph G = (V, E) with weight function w: E → R, where w(u, v) ≥ 0 for all (u, v) ∈ E.
• The vertices correspond to cities and the arcs to one-way roads.
• The label of a vertex is the name of a city.
• The arc (u, v) leads from the vertex u corresponding to the starting city to the vertex v corresponding to the city that is the end of the road.
• The weight of the arc is the length of the road.
• A path is a sequence of vertices of the graph.
• A simple path is a path in which no vertex and no edge are repeated.
• The length of a path connecting vertex u and any of other vertices is the sum of lengths of roads of this path, i.e. the sum of weights of graph arcs.
• To find the maximal length of a path from a given city u to city v in a given road system S, we first have to make sure that at least one path exists from city u to city v. If such a path exists, then to find the maximum length of the path you need to determine the lengths of roads. We will sequentially look through the vertices of graph G starting from vertex u and look for paths (by calculating their lengths) from the starting vertex to vertex v until all paths leading to vertex v have been looked through. If vertex v is not reachable from vertex u, then there is no maximal path from u to v. To keep the found path simple, we will memorize the traversed vertices in the current path.
• There can be several paths that satisfy the problem condition. To answer the question what is the maximal length of the path between two cities A and B, it is sufficient to find any of such paths (the last detected in the sequential order) and specify its length.

Formal problem statement

• In a weighted, labeled, cyclic, not necessarily connected graph find the length of the longest simple path between two vertices.
• If the road system consists of several connectivity components, then the desired path between two given cities will not exist if both given cities are in different connectivity components.
• If a one-way road system contains only one city, or no departure and/or destination city, or the departure city is the same as the destination city, then there is no path to be sought.
• If the one-way road system contains only two cities (departure and destination), then the problem is reduced to finding the longest road from the departure city to the destination city. Since in this problem it makes sense to save only the maximum of multiples of the road, the saved road will be the desired path.
• If the system of one-way roads has more than two cities, then to find the maximum length of the path between the given cities we will look through the graph in depth, starting from the top of start (the beginning of the path). We will mark the vertices with labels as they pass through. The label will tell us if the vertex has been viewed before. We will return when every vertex adjacent to the current vertex is tagged or is the end of the path. The search ends when all paths from vertex start to vertex finish have been viewed.
• The solution to this problem is to look at all paths from the next vertex adjacent to the start-city vertex to the destination-city vertex, which provides finding the path of maximal length.

An algorithm for solving the problem

{
   max ← 0, Road ← ∅;
   switch (enter information about the road system and create a graph adjacencies structure)
   {
      case 0:
         if (there are no simple ways out of the departure city)
            output "There are no simple ways out of the departure city";
         else
            if (number of cities == 2)
            {
               max ← the length of the road from the departure city to the destination city;
               Road ← road from the departure city to the destination city;
               output max, Road;
            }
            else
            {
               Road ← search for the maximum simple path between the given cities;
               max ← length of Road;
               if (max = 0)
                  output "There is no way from the departure city to the destination city";
               else
                  output max, Road;
               clearing the memory allocated for path storage;
            }
         break;
      case -1:
         output "The file with information about the road system was not found";
         break;
      case -2:
         output "The file with information about the road system is empty";
         break;
      case -3:
         output "The departure city is the same as the destination city";
         break;
     case -4:
         output "Departure city and/or destination city not found in the way";
         break;
   }
   clearing the memory allocated for storing the list of cities and the list of adjacencies;
}

An algorithm for finding the maximal path from vertex start to vertex finish

• S is a stack. An element of the stack is a vertex, its distance and a pointer to the list of viewed vertices reachable from it.
• Road is the path found.
• w is the current distance.

{
   S ← ∅; Road ← ∅;
   start ← start of the road;
   finish ← end of the road;
   x ← an unseen top adjacent to the start;
   while (∃x)
   {
      if (x == finish)
      {
         if (w > max)
         {
            clear the path already saved;
            max ← w;
         }
         if (∃ other unseen vertices adjacent to the start)
            x ← adjacent vertex;
         else
            mark x as a viewed vertex;
      }
      in_stack (S, x, w);
      while (S is not empty)
      {
         x ← the first element of S;
         y ← unseen vertex adjacent to x;
         if (y is not exist)
            from_stack(S);
         else
            if (y == finish) 
            {
               if (distance from start to y > max)
               {
                  max ← distance from start to y;
                  Road ← road from start to y;
               }
               from_stack(S);
            }
            else
            {
               mark y as a viewed vertex;
               in_stack (S, y, distance from start to y);
            }
      }
      x ← unseen vertex adjacent to start;
   }
   return Road;
}

Road system input algorithm

• BR is the beginning of the road.
• ER is the end of the road.
• start is the index of the departure city in the list of cities.
• finish is the index of the destination city in the list of cities.

{
   if (the file did not open) return -1;
   if (could not read the departure city) return -2;
   enter the departure city and the destination city;
   if (departure city == destination city) return -3;
   while (not end of file)
   {
      input of BR;
      if (BR is not on the list of cities)
         add BR to the list of cities;
      input of ER;
      if (ER is not on the list of cities)
         add ER to the list of cities;
      input of the road length from BR to ER;
      if (the road is not a loop && does not go to the departure city && does not go from the destination city)
         if (the road from BR to ER is not on the list of adjacencies)
            add the road from BR to ER to the list of adjacencies;
         else
            if (current road length > the length of the existing road from the BR to the ER)
              the length of the existing road from the BR to the ER ← current road length;
   }
   for (i ← 0; i < number of cities && count != 2; i++)
      if (cities[i] == departure city)
      {
         start = i;
         count++;
      }
      else
         if (cities[i] == destination city)
         {
            finish = i;
            count++;
         }
   if (count != 2) return -4;
   return 0;
}

Test 1

Purpose: The file with information about the road system was not found.
Input:

Result:
The file with information about the road system was not found

Test 2

Purpose: The file with information about the road system is empty.
Input:

Result:
The file with information about the road system is empty

Test 3

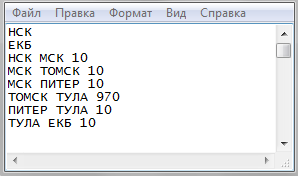
Purpose: There are no simple ways out of the departure city.
Input:
НСК
ЕКБ
ЕКБ ЕКБ 10
НСК НСК 10

Result:
There are no simple ways out of the НСК

Test 4

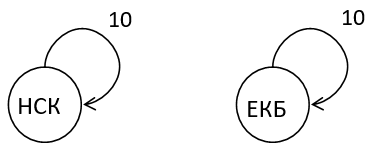
Purpose: There is no way from the departure city to the destination city.
Input:
НСК
ЕКБ
НСК ТУЛА 10
ТУЛА ПИТЕР 10
ПЕРМЬ ЕКБ 10

Result:
There is no way from the НСК to the ЕКБ

Test 5

Purpose: The departure city is the same as the destination city.
Input:
НСК
НСК
НСК ТУЛА 10
ТУЛА ПИТЕР 10
ПИТЕР ЕКБ 10

Result:
The departure city is the same as the destination city

Test 6

Purpose: Destination city is not on the way.
Input:
НСК
ЕКБ
НСК ТУЛА 10
ТУЛА ПИТЕР 10
ПЕРМЬ УФА 10

Result:
Departure city and/or destination city not found in the way

Test 7

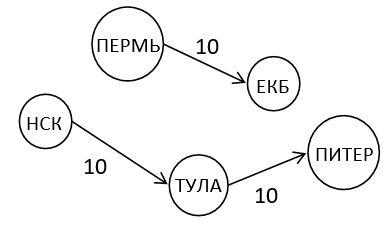
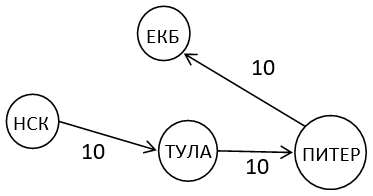
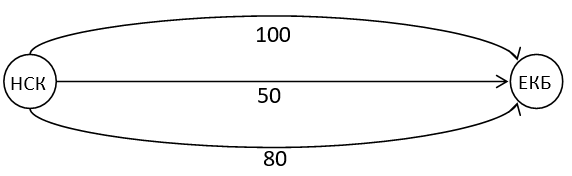
Purpose: There are multiple roads of different lengths between the two cities in the road system.
Input:
НСК
ЕКБ
НСК ЕКБ 80
НСК ЕКБ 100
НСК ЕКБ 50

Result:
The length of the maximum simple path from НСК to ЕКБ is 100
The longest simple path from НСК to ЕКБ: НСК — ЕКБ

Test 8

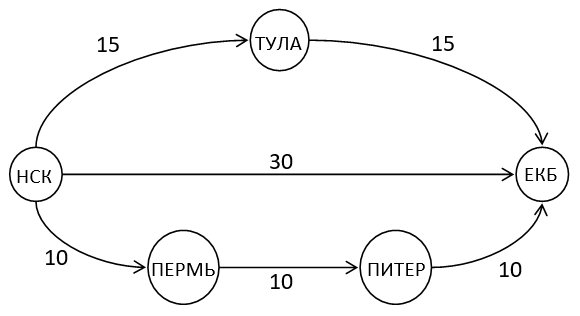
Purpose: All paths between the departure and destination cities are the same length.
Input:
НСК
ЕКБ
НСК ЕКБ 30
НСК ТУЛА 15
ТУЛА ЕКБ 15
НСК ПЕРМЬ 10
ПЕРМЬ ПИТЕР 10
ПИТЕР ЕКБ 10

Result:
The length of the maximum simple path from НСК to ЕКБ is 30
The longest simple path from НСК to ЕКБ: НСК — ПЕРМЬ — ПИТЕР — ЕКБ

Test 9

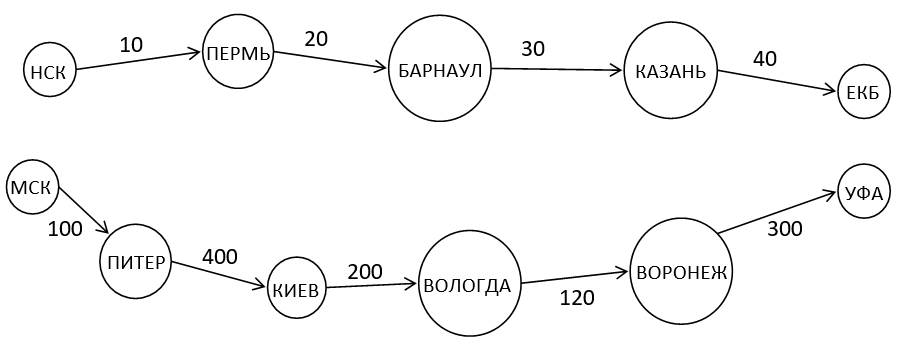
Purpose: The road system consists of several connectivity components.
Input:
НСК
ЕКБ
МСК ПИТЕР 100
ПИТЕР КИЕВ 400
КИЕВ ВОЛОГДА 200
ВОЛОГДА ВОРОНЕЖ 120
ВОРОНЕЖ УФА 300
НСК ПЕРМЬ 10
ПЕРМЬ БАРНАУЛ 20
БАРНАУЛ КАЗАНЬ 30
КАЗАНЬ ЕКБ 40

Result:
The length of the maximum simple path from НСК to ЕКБ is 100
The longest simple path from НСК to ЕКБ: НСК — ПЕРМЬ — БАРНАУЛ — КАЗАНЬ — ЕКБ

Test 10

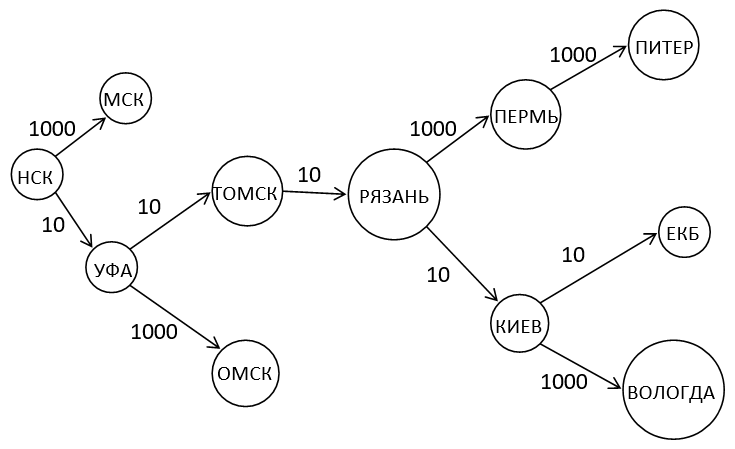
Purpose: The road system has dead-ends.
Input:
НСК
ЕКБ
НСК УФА 10
УФА ОМСК 1000
НСК МСК 1000
УФА ТОМСК 10
ТОМСК РЯЗАНЬ 10
РЯЗАНЬ ПЕРМЬ 1000
ПЕРМЬ ПИТЕР 1000
РЯЗАНЬ КИЕВ 10
КИЕВ ВОЛОГДА 1000
КИЕВ ЕКБ 10

Result:
The length of the maximum simple path from НСК to ЕКБ is 50
The longest simple path from НСК to ЕКБ: НСК — УФА — ТОМСК — РЯЗАНЬ — КИЕВ — ЕКБ

Test 11

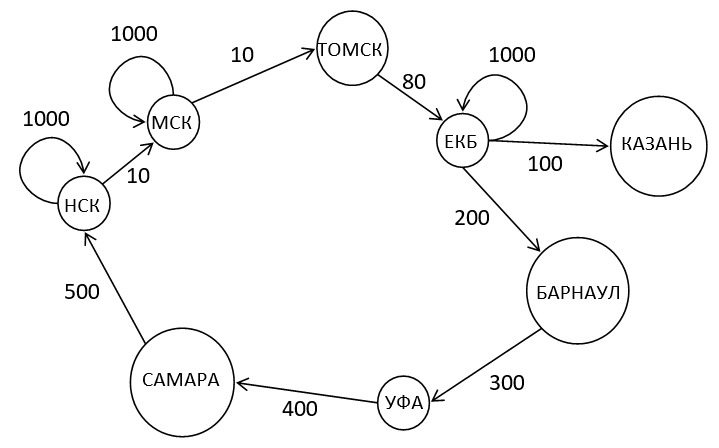
Purpose: The road system has loops, roads from the destination city and roads to the departure city.
Input:
НСК
ЕКБ
НСК МСК 10
НСК НСК 1000
МСК МСК 1000
ТОМСК ЕКБ 80
МСК ТОМСК 10
ЕКБ ЕКБ 1000
САМАРА НСК 500
ЕКБ КАЗАНЬ 100
ЕКБ БАРНАУЛ 200
БАРНАУЛ УФА 300
УФА САМАРА 400

Result:
The length of the maximum simple path from НСК to ЕКБ is 100
The longest simple path from НСК to ЕКБ: НСК — МСК — ТОМСК — ЕКБ

Test 12

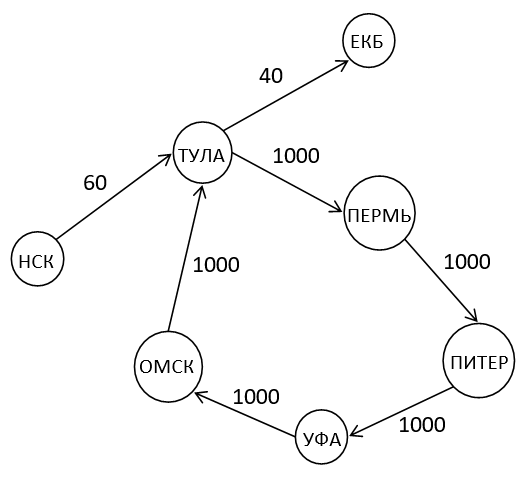
Purpose: The road system contains a cycle.
Input:
НСК
ЕКБ
НСК ТУЛА 60
ТУЛА ПЕРМЬ 1000
ПЕРМЬ ПИТЕР 1000
УФА ОМСК 1000
ПИТЕР УФА 1000
ОМСК ТУЛА 1000
ТУЛА ЕКБ 40

Result:
The length of the maximum simple path from НСК to ЕКБ is 100
The longest simple path from НСК to ЕКБ: НСК — ТУЛА — ЕКБ

Test 13

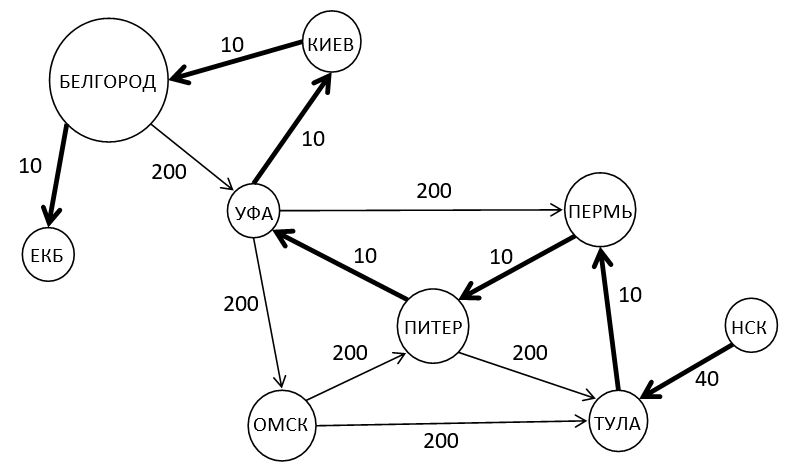
Purpose: The road system contains several cycles.
Input:
НСК
ЕКБ
НСК ТУЛА 40
ТУЛА ПЕРМЬ 10
ПЕРМЬ ПИТЕР 10
ПИТЕР ТУЛА 1000
ОМСК ТУЛА 1000
ОМСК ПИТЕР 1000
УФА ОМСК 1000
УФА ПЕРМЬ 1000
ПИТЕР УФА 10
УФА КИЕВ 10
БЕЛГОРОД УФА 1000
БЕЛГОРОД ЕКБ 10
КИЕВ БЕЛГОРОД 10

Result:
The length of the maximum simple path from НСК to ЕКБ is 100
The longest simple path from НСК to ЕКБ: НСК — ТУЛА — ПЕРМЬ — ПИТЕР — УФА — КИЕВ — БЕЛГОРОД — ЕКБ

Test 14

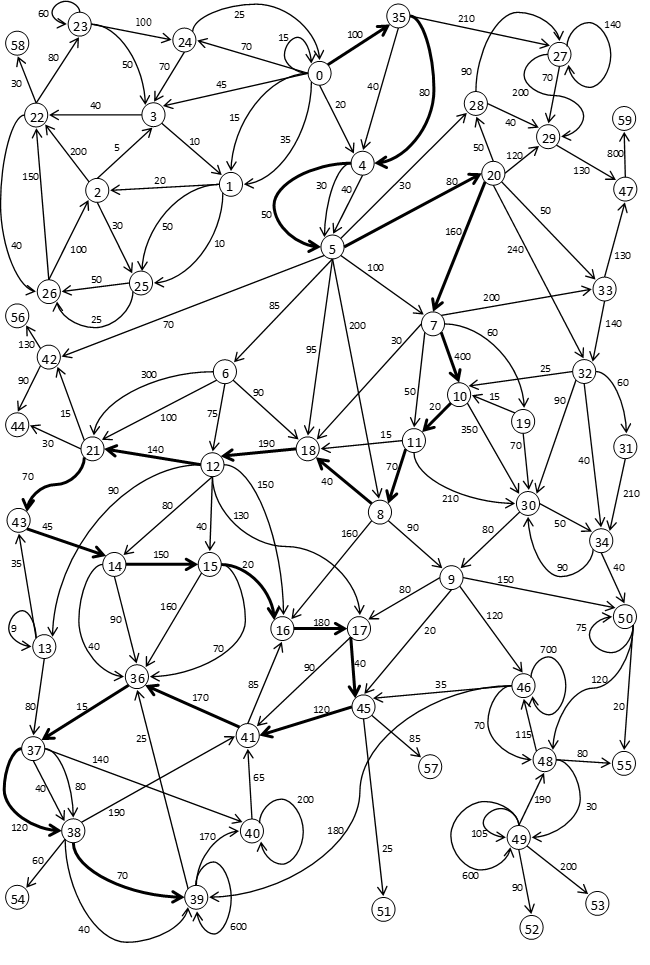
Purpose: A big test with all possible situations.
Input:
* too large for README, watch Input.txt *

Result:
The length of the maximum simple path from 0 to 39 is 2330
The longest simple path from 0 to 39: 0 — 35 — 4 — 5 — 20 — 7 — 10 — 11 — 8 — 18 — 12 — 21 — 43 — 14 — 15 — 16 — 17 — 45 — 41 — 36 — 37 — 38 — 39