NOIP2018 原创模拟题 T2
NOIP DAY1 T2 or DAY2 T2 难度
题目背景改编自小说《哈利波特与密室》。
说明:#4,bug经修复,感谢:@唐子川
哈利与罗恩进入了密室,他们发现密室由n个小室组成,所有小室编号分别为:1,2,...,n。所有小室之间有m条通道,对任意两个不同小室最多只有一条通道连接,而每通过一条通道都需要Ci 的时间。
开始时哈利与罗恩都在编号为1的小室里,他们的目标是拯救金妮和寻找日记,但是他们发现金妮和日记可能在两个不同的小室里,为了尽快发现真相,他们决定以最少的时间到达两个目标小室。但是某些小室只有会与蛇对话的人才能进入,也就是只有哈利一个人可以进入。
现在,哈利告诉你密室的结构,请你计算他们到达两个目标小室的最短时间。
第一行 n,m,k 表示有n个小室m条通道,k间小室只有哈利可以进入。
第二行 k 个数,表示只有哈利可以进入的小室的编号。(若k=0,不包含该行)
接下来m行,每行3个数:a,b,c 表示a小室与b小室之间有一条需要花费c时间的通道。
最后一行,两个数 x,y 表示哈利与罗恩需要去的小室的编号
一行,输出一个数,表示到达两个密室的最短时间。
6 8 1
5
1 2 3
2 3 2
1 3 4
3 4 1
4 6 5
5 6 2
1 6 6
1 5 3
4 6
5
10 13 3
3 4 10
1 2 1
2 3 2
3 4 3
4 5 4
5 6 5
6 7 10
7 8 5
8 9 10
9 10 3
10 1 2
1 9 6
3 8 10
4 6 3
6 8
16
哈利:1->5->6 花费时间为5
罗恩:1->3->4 花费时间为5
所以最短时间为5
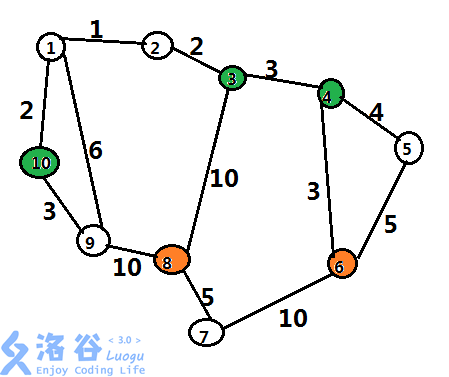
如图,橙色表示目标小室,绿色只有哈利可以通过
哈利:1->2->3->4->6 花费时间为9
罗恩:1->9->8 花费时间为16
所以最短时间为16
10% 数据满足:n<=5
30% 数据满足:n<=20
50% 数据满足:n<=1000
70% 数据满足:n<=10000
100%数据满足:n<=50000 ; a,b,k<=n c<=1000 ;m<=100000,保证罗恩可以在密室1
30%数据满足:k=0
Dijkstra计算最短距离,扩展邻接点时判断该顶点是否可达(对Harry所有顶点可达,对Ron可能有顶点不可达)。
dijkstra中使用accessible数组判断顶点是否可达。
对于到达两个目的地x和y的时间有几种情况,其中最小的时间即所求答案:
-
Harry到达x,Ron到达y,两者中较大的时间
-
Harry到达y,Ron到达x,两者中较大的时间
-
Harry一个人到达x和y,又有两种情况,取其中小的:
-
Harry先到达x再到达y
-
Harry先到达y再到达x
在Ron存在不可达顶点,即Harry到达一个顶点的最短距离可能小于Ron到达该顶点的最短距离,这种方法可能更快
-
-
Ron一个人到达x和y,但Ron到达一个顶点的最短距离不可能小于Harry到达该顶点的最短距离,所以这种方法不用考虑
#include <cstdio>
#include <cstdlib>
#include <vector>
#include <queue>
using namespace std;
typedef unsigned short vertex_t; //顶点类型(输入数据最大50000)
typedef unsigned short weight_t; //图的边权重类型(输入数据最大1000)
typedef unsigned int dist_t; //距离类型(边权重最大1000,但两点之间的距离可能超出65535)
//dist_t可能的最大值
#define DIST_T_INF 0xffffffff
//邻接点结构体
struct AdjNode {
vertex_t adj_v; //邻接顶点
weight_t adj_weight; //邻接边权重
AdjNode(vertex_t adj_v, weight_t adj_weight) : adj_v(adj_v), adj_weight(adj_weight) {}
};
//Dijkstra
class Dijkstra {
public:
/*
计算最短距离
@param graph 图
@param n 顶点数,顶点编号0~n-1
@param src 源
@param des 终点
@param accessible 数组,表示一个顶点是否可达
@return dist_t 返回src与des之间的最短距离
*/
dist_t minDist(vector<AdjNode>* graph, size_t n, vertex_t src, vertex_t des, bool * accessible);
private:
//优先队列存储的结构体
struct PriorityNode {
vertex_t v; //顶点
dist_t dist; //源与v的距离
PriorityNode(vertex_t v, dist_t dist) : v(v), dist(dist) {}
//优先队列用于比较的结构体
struct cmp {
bool operator() (PriorityNode& a, PriorityNode& b) {
return a.dist > b.dist;
}
};
};
private:
//成员变量
dist_t * dist_; //dist_[v]为当前src与v的最短距离
bool * collected_; //collected_[v]表示当前v是否收录
priority_queue<PriorityNode, vector<PriorityNode>, PriorityNode::cmp> pqueue_; //优先队列
};
dist_t Dijkstra::minDist(vector<AdjNode>* graph, size_t n, vertex_t src, vertex_t des, bool * accessible) {
//dijkstra算法
dist_ = new dist_t[n];
fill(dist_, dist_ + n, DIST_T_INF); //初始化
collected_ = new bool[n];
fill(collected_, collected_ + n, false); //初始化
dist_[src] = 0;
pqueue_.push(PriorityNode(src, 0));
vertex_t top_v, adj_v;
dist_t tmp_dist;
while (!pqueue_.empty()) {
top_v = pqueue_.top().v; //当前与src距离最小的顶点出队列
pqueue_.pop();
if (collected_[top_v]) continue;
collected_[top_v] = true;
if (top_v == des) {
//到达终点
while (!pqueue_.empty()) pqueue_.pop();
break;
}
for (auto it = graph[top_v].begin(); it != graph[top_v].end(); it++) { //遍历邻接点
adj_v = it->adj_v; //邻接点
if (!accessible[adj_v]) continue; //若adj_v不可达,则continue
if (!collected_[adj_v]) {
//此时adj_v没被收录,即src到adj_v的最短距离还未确定
tmp_dist = dist_[top_v] + (dist_t)it->adj_weight; //tmp_dist = src到top_v的距离 + top_v到adj_v的距离
if (tmp_dist < dist_[adj_v]) {
//更新
dist_[adj_v] = tmp_dist;
pqueue_.push(PriorityNode(adj_v, tmp_dist));
}
}
} //for
} //while
//若src不可达des,则dist_[des]为DIST_T_INF
dist_t result = dist_[des];
//释放内存
free(dist_);
free(collected_);
return result;
}
int main() {
int n, m, k;
scanf("%d %d %d", &n, &m, &k);
bool * accessible = new bool[n];
//初始化所有顶点可达
fill(accessible, accessible + n, true);
size_t i;
if (k) {
int room;
for (i = 0; i < k; i++) {
scanf("%d", &room);
//该顶点(房间)仅Harry可达,对Ron来说不可达
//输入顶点编号为 1~n,改为0~n-1
accessible[room - 1] = false;
}
}
vector<AdjNode> * graph = new vector<AdjNode>[n];
int a, b, c;
for (i = 0; i < m; i++) {
//插入边
scanf("%d %d %d", &a, &b, &c);
a--; b--; //顶点编号改为从0开始
graph[a].push_back(AdjNode((vertex_t)b, (weight_t)c));
graph[b].push_back(AdjNode((vertex_t)a, (weight_t)c));
}
scanf("%d %d", &a, &b);
//des_x和des_y为需要到达的两个目的地
vertex_t des_x = a - 1, des_y = b - 1; //编号改为从0开始
Dijkstra dijkstra;
//先计算Ron到达des_x与des_y的最短距离,因为此时accessible中Ron不可达的顶点已经标记为false了
dist_t ron_x = dijkstra.minDist(graph, n, 0, des_x, accessible); //Ron到达des_x的最短距离(时间)
dist_t ron_y = dijkstra.minDist(graph, n, 0, des_y, accessible); //Ron到达des_y的最短距离(时间)
dist_t harry_x, harry_y, harry_x_y;
if (k) { //若存在只能Harry走的顶点
fill(accessible, accessible + n, true); //所有顶点Harry均可达
harry_x = dijkstra.minDist(graph, n, 0, des_x, accessible); //Harry到达des_x的最短距离(时间)
harry_y = dijkstra.minDist(graph, n, 0, des_y, accessible); //Harry到达des_y的最短距离(时间)
harry_x_y = dijkstra.minDist(graph, n, des_x, des_y, accessible); //Harry从x走到y的最短距离(时间)
}
else { //若不存在只能Harry走的顶点
//所有顶点Harry与Ron都可达,Harry到达任意一个顶点的最短距离与Ron到达该顶点的最短距离相同
harry_x = ron_x;
harry_y = ron_y;
}
dist_t result = DIST_T_INF; //结果
result = min(result, max(harry_x, ron_y)); //Harry去des_x, Ron去des_y
result = min(result, max(harry_y, ron_x)); //Harry去des_y, Ron去des_x
if (k) {
//des_x,des_y都由Harry一个人去,
//(Harry先到des_x再到des_y或者先到des_y再到des_x)
//在存在只有Harry可达的顶点时,这种方式才可能更快
result = min(result, min(harry_x + harry_x_y, harry_y + harry_x_y));
}
printf("%u", result);
free(accessible);
for (i = 0; i < n; i++)
vector<AdjNode>().swap(graph[i]);
return 0;
}