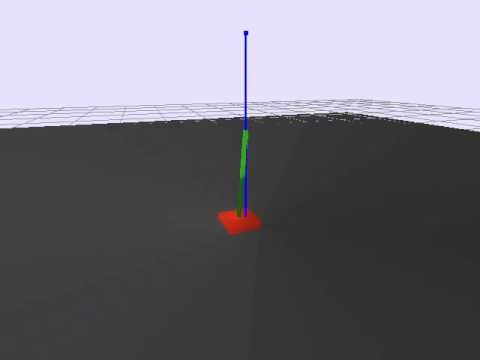
cartpole++ is a non trivial 3d version of cartpole simulated using bullet physics where the pole isn't connected to the cart.
this repo contains a gym env for this cartpole as well as implementations for training with ...
- likelihood ratio policy gradients ( lrpg_cartpole.py ) for the discrete control version
- deep deterministic policy gradients ( ddpg_cartpole.py ) for the continuous control version
- normalised advantage functions ( naf_cartpole.py ) also for the continuous control version
we also train a deep q network from keras-rl as an externally implemented baseline.
for more info see the blog post. for experiments more related to potential transfer between sim and real see drivebot. for next gen experiments in continuous control from pixels in minecraft see malmomo
episodes are initialised with the pole standing upright and receiving a small push in a random direction
episodes are terminated when either the pole further than a set angle from vertical or 200 steps have passed
there are two state representations available; a low dimensional one based on the cart & pole pose and a high dimensional one based on raw pixels (see below)
there are two options for controlling the cart; a discrete and continuous method (see below)
reward is simply 1.0 for each step in the episode
in both low and high dimensional representations we use the idea of action repeats; per env.step we apply the chosen action N times, take a state snapshot and repeat this R times. the deltas between these snapshots provides enough information to infer velocity (or acceleration (or jerk)) if the learning algorithm finds that useful to do.
observation state in the low dimensional case is constructed from the poses of the cart & pole
- it's shaped
(R, 2, 7) - axis 0 represents the R repeats
- axis 1 represents the object; 0=cart, 1=pole
- axis 2 is the 7d pose; 3d postition + 4d quaternion orientation
- this representation is usually just flattened to (R*14,) when used
the high dimensional state is a rendering of the scene
- it's shaped
(height, width, 3, R, C) - axis 0 & 1 are the rendering height/width in pixels
- axis 2 represents the 3 colour channels; red, green and blue
- axis 3 represents the R repeats
- axis 4 represents which camera the image is from; we have the option of rendering with one camera or two (located at right angles to each other)
- this representation is flattened to have shape
(H, W, 3*R*C). we do this for ease of use of conv2d operations. (TODO: try conv3d instead)
in the discrete case the actions are push cart left, right, up, down or do nothing.
in the continuous case the action is a 2d value representing the push force in x and y direction (-1 to 1)
in all cases we give a reward of 1 for each step and terminate the episode when either 200 steps have passed or the pole has fallen too far from the z-axis
we use a random action agent (click through for video) to sanity check the setup.
add --gui to any of these to get a rendering
# no initial push and taking no action (action=0) results in episode timeout of 200 steps.
# this is a check of the stability of the pole under no forces
$ ./random_action_agent.py --initial-force=0 --actions="0" --num-eval=100 | ./deciles.py
[ 200. 200. 200. 200. 200. 200. 200. 200. 200. 200. 200.]
# no initial push and random actions knocks pole over
$ ./random_action_agent.py --initial-force=0 --actions="0,1,2,3,4" --num-eval=100 | ./deciles.py
[ 16. 22.9 26. 28. 31.6 35. 37.4 42.3 48.4 56.1 79. ]
# initial push and no action knocks pole over
$ ./random_action_agent.py --initial-force=55 --actions="0" --num-eval=100 | ./deciles.py
[ 6. 7. 7. 8. 8.6 9. 11. 12.3 15. 21. 39. ]
# initial push and random action knocks pole over
$ ./random_action_agent.py --initial-force=55 --actions="0,1,2,3,4" --num-eval=100 | ./deciles.py
[ 3. 5.9 7. 7.7 8. 9. 10. 11. 13. 15. 32. ]
$ ./dqn_cartpole.py \
--num-train=2000000 --num-eval=0 \
--save-file=ckpt.h5
result by numbers...
$ ./dqn_cartpole.py \
--load-file=ckpt.h5 \
--num-train=0 --num-eval=100 \
| grep ^Episode | sed -es/.*steps:// | ./deciles.py
[ 5. 35.5 49.8 63.4 79. 104.5 122. 162.6 184. 200. 200. ]
result visually (click through for video)
$ ./dqn_cartpole.py \
--gui --delay=0.005 \
--load-file=run11_50.weights.2.h5 \
--num-train=0 --num-eval=100
policy gradient nails it
$ ./lrpg_cartpole.py --rollouts-per-batch=20 --num-train-batches=100 \
--ckpt-dir=ckpts/foo
result by numbers...
# deciles
[ 13. 70.6 195.8 200. 200. 200. 200. 200. 200. 200. 200. ]
result visually (click through for video)
./ddpg_cartpole.py \
--actor-hidden-layers="100,100,50" --critic-hidden-layers="100,100,50" \
--action-force=100 --action-noise-sigma=0.1 --batch-size=256 \
--max-num-actions=1000000 --ckpt-dir=ckpts/run43
result by numbers
# episode len deciles
[ 30. 48. 56.8 65. 73. 86. 116.4 153.3 200. 200. 200. ]
# reward deciles
[ 35.51154724 153.20243076 178.7908135 243.38630372 272.64655323
426.95298195 519.25360223 856.9702368 890.72279221 913.21068417
955.50168709]
result visually (click through for video)
./naf_cartpole.py --action-force=100 \
--action-repeats=3 --steps-per-repeat=4 \
--optimiser=Momentum --optimiser-args='{"learning_rate": 0.0001, "momentum": 0.9}' \
similiar convergence to ddpg
does OK, but not perfect yet. as a human it's hard to do even... (see the blog post)
run a random agent, logging events to disk (outputs total rewards per episode)
note: for replay logging will need to compile protobuffer protoc event.proto --python_out=.
$ ./random_action_agent.py --event-log=test.log --num-eval=10 --action-type=continuous
12
14
...
review event.log (either from ddpg training or from random agent)
$ ./event_log.py --log-file=test.log --echo
event {
state {
cart_pose: 0.116232253611
cart_pose: 0.0877446383238
cart_pose: 0.0748709067702
cart_pose: 1.14359036161e-05
cart_pose: 5.10180834681e-05
cart_pose: 0.0653914809227
cart_pose: 0.997859716415
pole_pose: 0.000139251351357
pole_pose: -0.0611916743219
pole_pose: 0.344804286957
pole_pose: -0.123383037746
pole_pose: 0.00611496530473
pole_pose: 0.0471726879478
pole_pose: 0.991218447685
render {
height: 120
width: 160
rgba: "\211PNG\r\n\032\n\000\..."
}
}
is_terminal: false
action: -0.157108291984
action: 0.330988258123
reward: 4.0238070488
}
...
generate images from event.log
$ ./event_log.py --log-file=test.log --img-output-dir=eg_renders
$ find eg_renders -type f | sort
eg_renders/e_00000/s_00000.png
eg_renders/e_00000/s_00001.png
...
eg_renders/e_00009/s_00018.png
eg_renders/e_00009/s_00019.png
1000 events in an event_log is roughly 750K for the high dim case and 100K for low dim