This library provides a simple interface to the SIMD primops provided in GHC 7.8. SIMD (Single Instruction Multiple Data) CPU instructions provide an easy way to parallelize numeric computations. GHC 7.8 provides primops that let us access these CPU instructions. This package wraps thos primops in a more user friendly form. These primops can only be used with the llvm backend, so you must have llvm installed and compile any program using this library with the -llvm option.
This library is available on hackage, and so can be installed by:
cabal update
cabal install simd
We can write a non-SIMD function to calculate the Euclidean distance as:
distance :: VU.Vector Float -> VU.Vector Float -> Float
distance !v1 !v2 = sqrt $ go 0 (VG.length v1-1)
where
go tot (-1) = tot
go tot i = go tot' (i-1)
where
tot' = tot+diff1*diff1
diff1 = v1 `VG.unsafeIndex` i-v2 `VG.unsafeIndex` i
To take advantage of the SIMD operations, we first convert the vector from type VU.Vector Float into VU.Vector (X4 Float) using unsafeVectorizeUnboxedX4.
We then perform our SIMD operations.
X4 Float is an instance of the Num type class, so this is straightforward.
Finally, we convert our X4 Float into a single Float using the plusHorizontalX4 command.
Horizontal additions are costly and should be avoided except as the final step in a SIMD computation.
distance_simd4 :: VU.Vector Float -> VU.Vector Float -> Float
distance_simd4 v1 v2 = sqrt $ plusHorizontalX4 $ go 0 (VG.length v1'-1)
where
v1' = unsafeVectorizeUnboxedX4 v1
v2' = unsafeVectorizeUnboxedX4 v2
go tot (-1) = tot
go tot i = go tot' (i-1)
where
tot' = tot+diff*diff
diff = v1' `VG.unsafeIndex` i - v2' `VG.unsafeIndex` i
The X4 above stands for how many operations we want to do in parallel using SIMD.
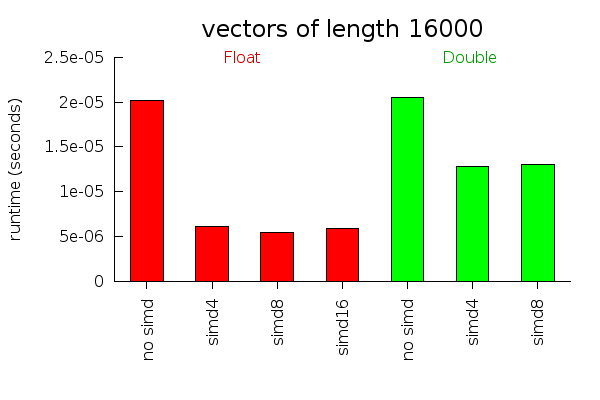
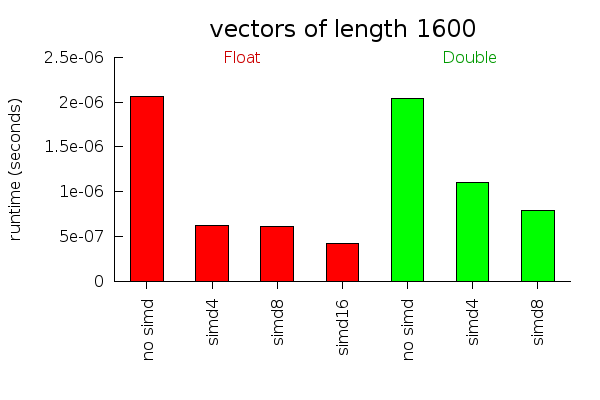
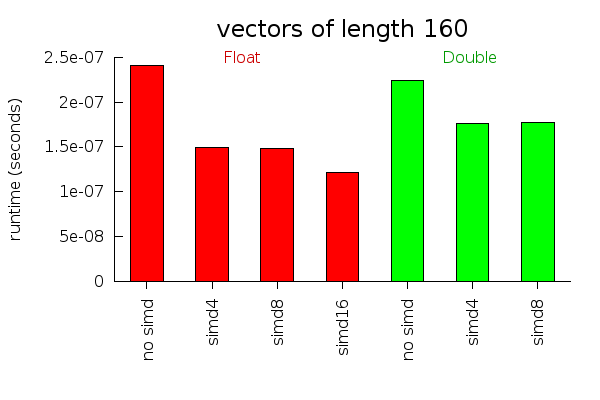
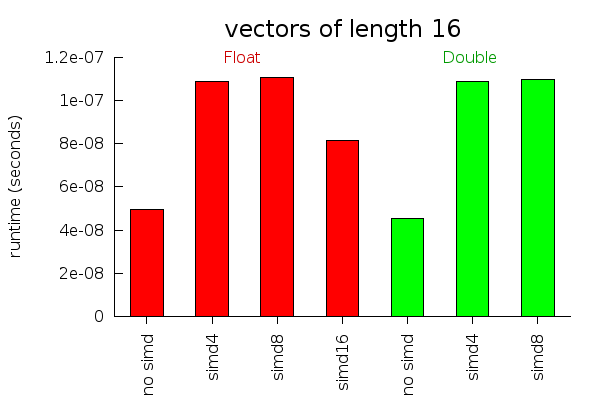
We could also choose X8 and X16, but as the performance graphs below demonstrate, these do not provide as much of a speed up as you might hope.
More examples of Euclidean distance functions (some of which perform very bad!) can be found in the criterion benchmark in the examples folder.
These performance graphs measure how long it takes to calculate the Euclidean distance between two vectors of different lengths. For large vectors, almost all the work can be done in parallel and SIMD instructions work very well. For small vectors, non parallelizable instructions and initialization overhead become more important. For vectors of size 16, we actually run slower using the simd operations. I suspect with some fiddling around, this overhead could be reduced. But I don't ever use vectors that small, so I didn't bother trying.
Performance tests will vary a lot depending on what computer you are using and what instructions it supports well. I ran these tests on my 64 bit Core 2 Duo laptop.
It might be useful to provide some rewrite rules to make vectorization an automatic performance improvement. This is not easy to do with the current Data.Vector API, however, because all the vector operations get inlined before the rules can fire. In any case, people who care enough about performance to want SIMD instructions will probably want to write the SIMD code manually.
Finally, I wasn't part of the work on the GHC side of SIMD operations. They did all the hard work. Thanks!