Dijkstra's algorithm in PHP

This README.md file describes a PHP implementation of Dijkstra's algorithm, a way to find the shortest path between one node and all the other in a [directed or undirected] graph.

Source: Wikipedia

In this implementation it is possible to indicate whether the graph is directed or undirected. If directed, it is not possible to review only non-visited nodes. That's why it is important to indicate this fact. By default, this implementation considers that the graph is undirected but, of course, there are very simple methods to calculate this.

Also, this implementation makes use of a Priority Queue, which represents a small performance optimization, but very important when dealing with a huge amount of nodes.

Example graph

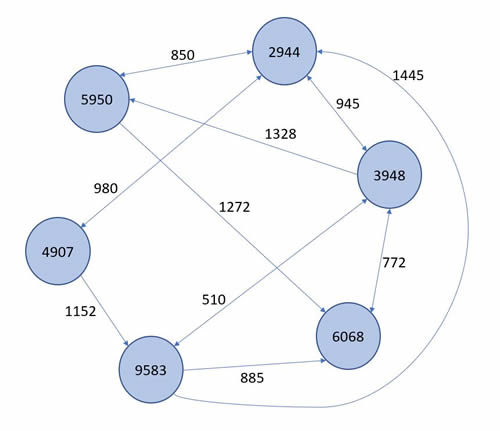
This implementation comes with an example in order to test it. This is the graph:

The graph can be found in the data.csv file. When you execute the script it will calculate all shortest paths from source with ID 5950.

Shortest path

The algorithm is designed to find the shortest paths from the origin vertex (the source) to all the other vertices. The result is stored in a couple of arrays (distances and previous) but those arrays are clearly not "human readable". To solve this problem I have written a method called shortestPathTo(), which returns an array with the shortest path from source to destination.

In the example graph, the shortes path from 5950 to 9583 is like this:

Node	Weight	Acc. weight
5950	0	0
2944	850	850
3948	945	1795
9583	510	2305

It's returned in an array with the following structure, much more human readable:

|-- [0]
     |-- [node_identifier] => 5950
     |-- [weight] => 0
     |-- [accumulated_weight] => 0
|-- [1]
     |-- [node_identifier] => 2944
     |-- [weight] => 850
     |-- [accumulated_weight] => 850
|-- [2]
     |-- [node_identifier] => 3948
     |-- [weight] => 945
     |-- [accumulated_weight] => 1795
|-- [3]
     |-- [node_identifier] => 9583
     |-- [weight] => 510
     |-- [accumulated_weight] => 2305

Implementation decisions

• The graph is represented with an adjacency list (not a matrix) as it is sparse.
• The graph is passed by reference, in order to save memory and speed up the whole process.
• The __construct method not only initializes the data structures, but also runs the algorithm.

Installation

First, clone this repository:

$ git clone https://github.com/oscarpascualbakker/dijkstra.git .

Then, run the commands to build and run the Docker image:

$ docker build -t dijkstra .
$ docker container run --rm -v %cd%:/usr/src/dijkstra/ dijkstra php dijkstra.php

(use %cd% on Windows, or ${PWD} on Mac)

Tests can be run this way:

$ docker container run -it --rm dijkstra vendor/bin/phpunit ./tests

Cost analysis

Time complexity analysis of this Dijkstra implementation, as stated in the Wikipedia, is:

• Without using a priority queue: O(|V|^2)
• Using a priority queue: O(|V| + |E| Log |V|)

(Where V is the number of vertices/nodes and E is the number of edges/connections.)

Let's make a couple of assumptions in order to calculate time complexity in directed graphs.

• Case 1: 6 nodes and 15 edges (our directed graph example)
• Case 2: 5.000 nodes and 10.000 edges

Case 1 results

Without priority queue: 6^2 = 36 executions Using a priority queue: 15 * Log 6 = 37 executions

In small graphs the usage of a priority queue makes no improvement.

Case 2 results

Without priority queue: 5.000^2 = 25.000.000 executions Using a priority queue: 10.000 * Log 5.000 = 123.000 executions

In big graphs, the usage of a priority queue has an enormous impact on the performance of Dijkstra's algorithm.

Obviously, 10.000 connections in a 5.000 nodes graph means it is a very sparse one. With denser graphs these calculations will change, but not very much. ;-)

Further improvements or TODO's

Check that there are no negative weights. If so, use Bellman-Ford algorithm, instead. Make it reusable, by assigning source dynamically. Decouple the Priority Queue from the implementation, so that the user can inject any other.

Comments

Dijkstra's shortest paths is a nice algorithm. It has only 9 lines in this implementation, without counting the initialization. Of course, behind the scenes there is a lot of stuff (e.g. the initialization, the priority queue, the shortest path response, ...). Also, this implementation is quite clear, easy to read. I hope you enjoy using it as much as I enjoyed writing it.

As usual, don't hesitate to give me your feedback. I'm glad to improve this algorithm with your help.

And if you like this code, why don't you buy me a coffee? :-)

Cheers!