import numpy as np
import matplotlib.pyplot as plt
from numpy.random import default_rng
from sklearn.model_selection import LeaveOneOut, GridSearchCV
from sklearn.linear_model import LinearRegressionimport matplotlib.pyplot as plt
%matplotlib inline
plt.axis('off')
plt.arrow(0, 0, 1.0, 0.0, head_width=0.05, head_length=0.1, fc='k', ec='k'); plt.figtext(0.90, 0.25, r'$f_1$', fontsize=26)
plt.arrow(0, 0, 0.4, 0.6, head_width=0.05, head_length=0.1, fc='k', ec='k'); plt.figtext(0.50, 0.70, r'$f_2$', fontsize=26)
plt.arrow(0, 0, 0.9, -0.2, head_width=0.05, head_length=0.1, fc='tab:blue' , ec='tab:blue' ); plt.figtext(0.83, 0.10, r'$f_3$', fontsize=26)
plt.arrow(0, 0, 0.0, 0.8, head_width=0.05, head_length=0.1, fc='tab:blue' , ec='tab:blue' ); plt.figtext(0.10, 0.90, r'$f_4$', fontsize=26)
plt.arrow(0, 0, 0.7, 0.4, head_width=0.05, head_length=0.1, fc='tab:orange', ec='tab:orange'); plt.figtext(0.70, 0.55, r'$y$', fontsize=26)
plt.show()
According to the above image, we define four feature vectors
,
,
,
and
.
The response
lies in the plane defined by the first two feature vectors
and
.
f1 = np.array([1.0, 0.0, 0.0])
f2 = np.array([0.0, 1.0, 0.0])
f3 = np.array([1.0, -0.2, 0.0])
f4 = np.array([0.0, 0.0, 1.0])
y = np.array([1.0, 1.0, 0.0])We study the length of the OLS solution, which for
is
given by the parameter vector with minimum
-norm.
def OLSnorm(X, y):
return np.linalg.norm(np.linalg.pinv(X.T@X)@X.T@y)As baseline, we begin with the OLS solution if we are only given
and
:
OLSnorm(np.array([f1, f2]).T, y)1.4142135623730951
The length of the solution decreases if we add another feature vector to X:
OLSnorm(np.array([f1, f2, f3]).T, y)1.2985663286116427
However, this is only the case if the feature vector is correlated with
:
OLSnorm(np.array([f1, f2, f4]).T, y)1.4142135623730951
data = np.array([
0.001399613, -0.23436656,
0.971629779, 0.64689524,
0.579119475, -0.92635765,
0.335693937, 0.13000706,
0.736736086, -0.89294863,
0.492572335, 0.33854780,
0.737133774, -1.24171910,
0.563693769, -0.22523318,
0.877603280, -0.12962722,
0.141426545, 0.37632006,
0.307203910, 0.30299077,
0.024509308, -0.21162739,
0.843665029, -0.76468719,
0.771206067, -0.90455412,
0.149670258, 0.77097952,
0.359605608, 0.56466366,
0.049612895, 0.18897607,
0.409898906, 0.32531750,
0.935457898, -0.78703491,
0.149476207, 0.80585375,
0.234315216, 0.62944986,
0.455297119, 0.02353327,
0.102696671, 0.27621694,
0.715372314, -1.20379729,
0.681745393, -0.83059624 ]).reshape(25,2)
y = data[:,1]
X = data[:,0:1]
plt.scatter(X[:,0], y)
plt.show()
We use the following linear regressor class for all double descent
examples. It takes only the first
columns from the
feature matrix
and
computes the minimum
-norm
solution when
.
class MyRidgeRegressor:
def __init__(self, p=3, alpha=0.0):
self.p = p
self.theta = None
self.alpha = alpha
def fit(self, F, y):
F = F[:, 0:self.p]
self.theta = np.linalg.pinv(F.transpose()@F + self.alpha*np.identity(F.shape[1]))@F.transpose()@y
def predict(self, F):
F = F[:, 0:self.p]
return F@self.theta
def set_params(self, **parameters):
for parameter, value in parameters.items():
setattr(self, parameter, value)
return self
def get_params(self, deep=True):
return {"p" : self.p, "alpha" : self.alpha}def evaluate_model(fg, X, y, n, ps, runs=10):
estimator = MyRidgeRegressor()
result = None
for i in range(runs):
F, y = fg(X, y, n, np.max(ps), random_state=i)
clf = GridSearchCV(estimator=estimator,
param_grid=[{ 'p': list(ps) }],
cv=LeaveOneOut(),
scoring="neg_mean_squared_error")
clf.fit(F, y)
if result is None:
result = -clf.cv_results_['mean_test_score']
else:
result += -clf.cv_results_['mean_test_score']
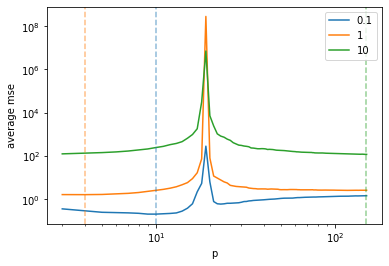
return result / runsThis example of double descent uses covariates generated from a
multivariate normal distribution, i.e. the
-th column of X is given
by
In order to obtain a double descent phenomenon, we need that some
are highly
correlated with
and the
remaining features are uncorrelated. Hence, we define
and generate observations
according to the linear
model
where
.
class RandomFeatures():
def __init__(self, scale = 1):
self.scale = scale
def __call__(self, X, y, n, p, random_state=42):
rng = default_rng(seed=random_state)
mu = np.repeat(0, n)
sigma = np.identity(n)
F = rng.multivariate_normal(mu, sigma, size=p).T
theta = np.array([ 1/(j+1) for j in range(p) ])
y = F@theta + rng.normal(0, self.scale, size=n)
return F, yps = range(3, 151)
scales = [0.1, 1, 10]
result = [ evaluate_model(RandomFeatures(scale=scale), None, None, 20, ps, runs=100) for scale in scales ]
result = np.array(result)p = plt.plot(ps, result.T)
[ plt.axvline(x=ps[np.argmin(result[i])], color=p[i].get_color(), alpha=0.5, linestyle='--') for i in range(result.shape[0]) ]
plt.legend(scales)
plt.xscale("log")
plt.yscale("log")
plt.xlabel("p")
plt.ylabel("average mse")
plt.show()
Increasing the number of features not always leads to an increase in
model complexity. There are several cases where adding more features
actually constraints the model, which we call here implicit
regularization. For instance, adding features to
that are uncorrelated
with
will generally
lead to a stronger regularization (e.g. when adding columns to
that are drawn from a
normal distribution). Here, we test a different strategy to increase
implicit regularization. We implement a function called
compute_noisy_polynomial_features that computes noisy polynomial
features
from
.
The
-th column of
is given by
where
,
denotes the maximum degree (max_degree parameter) and
is a vector of
independent draws from a normal distribution with mean
and standard deviation
. With
we denote the
-th power of each
element in
.
class NoisyPolynomialFeatures():
def __init__(self, max_degree = 15, scale = 0.1):
self.max_degree = max_degree
self.scale = scale
def __call__(self, X, y, n, p, random_state=42):
x = X if len(X.shape) == 1 else X[:,0]
rng = default_rng(seed=random_state)
F = np.array([]).reshape(x.shape[0], 0)
F = np.insert(F, 0, np.repeat(1, len(x)), axis=1)
for k in range(p):
d = (k % self.max_degree)+1
f = x**d + rng.normal(size=len(x), scale=self.scale)
F = np.insert(F, k+1, f, axis=1)
return F, yEvaluate the performance for
,
and
.
ps = range(3, 201)
scales = [0.01, 0.02, 0.05]
result = [ evaluate_model(NoisyPolynomialFeatures(scale=scale), X, y, len(y), ps, runs=100) for scale in scales ]
result = np.array(result)p = plt.plot(ps, result.T)
[ plt.axvline(x=ps[np.argmin(result[i])], color=p[i].get_color(), alpha=0.5, linestyle='--') for i in range(result.shape[0]) ]
plt.legend(scales)
plt.xscale("log")
plt.xlabel("p")
plt.yscale("log")
plt.ylim(0.1,10)
plt.ylabel("average mse")
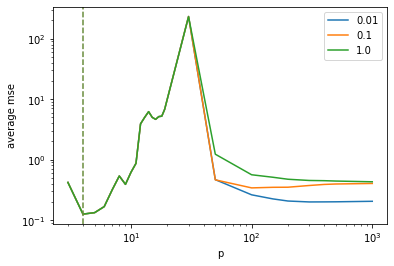
plt.show()
Another possibility to obtain double descent curves is to start off with
a standard polynomial regression task and to add random (uncorrelated)
features. The -th column
of
is given by
where denotes the
maximum degree of the polynomial features and
.
class PolynomialWithRandomFeatures():
def __init__(self, max_degree = 15, scale = 0.1):
self.max_degree = max_degree
self.scale = scale
def __call__(self, X, y, n, p, random_state=42):
x = X if len(X.shape) == 1 else X[:,0]
rng = default_rng(seed=random_state)
F = np.array([]).reshape(x.shape[0], 0)
# Generate polynomial features
for deg in range(np.min([p, self.max_degree+1])):
F = np.insert(F, deg, x**deg, axis=1)
if p <= self.max_degree+1:
return F, y
# Generate random features
for j in range(p - self.max_degree - 1):
f = rng.normal(size=F.shape[0], scale=self.scale)
F = np.insert(F, F.shape[1], f, axis=1)
return F, yps = list(range(3, 20)) + [30, 50, 100, 150, 200, 300, 400, 500, 1000]
scales = [0.01, 0.1, 1.0]
result = [ evaluate_model(PolynomialWithRandomFeatures(scale=scale), X, y, len(y), ps, runs=100) for scale in scales ]
result = np.array(result)p = plt.plot(ps, result.T)
[ plt.axvline(x=ps[np.argmin(result[i])], color=p[i].get_color(), alpha=0.5, linestyle='--') for i in range(result.shape[0]) ]
plt.legend(scales)
plt.xscale("log")
plt.xlabel("p")
plt.yscale("log")
#plt.ylim(0.1,10)
plt.ylabel("average mse")
plt.show()
class LegendrePolynomialFeatures():
def __call__(self, X, y, n, p, random_state=42):
x = X if len(X.shape) == 1 else X[:,0]
F = np.array([]).reshape(x.shape[0], 0)
# Generate polynomial features
for deg in range(p):
l = np.polynomial.legendre.Legendre([0]*deg + [1], domain=[0,1])
F = np.insert(F, deg, l(x), axis=1)
return F, yF, _ = LegendrePolynomialFeatures()(X, y, len(y), 1000)
g = np.linspace(0, 1, 10000)
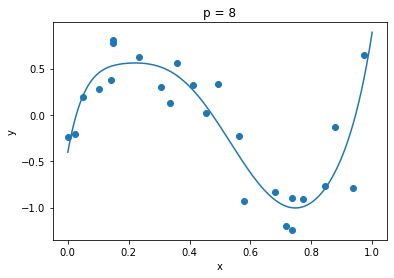
G, _ = LegendrePolynomialFeatures()(g, y, len(y), 1000)clf = MyRidgeRegressor(p=8)
clf.fit(F, y)
plt.plot(g, clf.predict(G))
plt.scatter(X, y)
plt.title("p = 8")
plt.xlabel("x")
plt.ylabel("y")
plt.show()
clf = MyRidgeRegressor(p=50)
clf.fit(F, y)
plt.plot(g, clf.predict(G))
plt.scatter(X, y)
plt.title("p = 100")
plt.xlabel("x")
plt.ylabel("y")
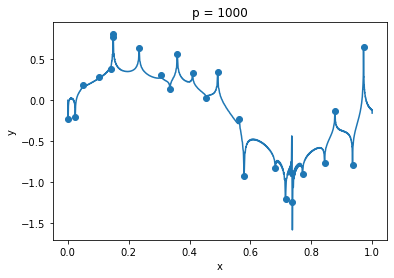
plt.show()
clf = MyRidgeRegressor(p=1000)
clf.fit(F, y)
plt.plot(g, clf.predict(G))
plt.scatter(X, y)
plt.title("p = 1000")
plt.xlabel("x")
plt.ylabel("y")
plt.show()
ps = list(range(3, 20)) + [30, 50, 100, 150, 200, 300, 400, 500, 1000]
result = evaluate_model(LegendrePolynomialFeatures(), X, y, len(y), ps, runs=1)p = plt.plot(ps, result)
plt.axvline(x=ps[np.argmin(result)], color=p[0].get_color(), alpha=0.5, linestyle='--')
plt.legend(scales)
plt.xscale("log")
plt.xlabel("p")
plt.yscale("log")
plt.ylim(0.1,10)
plt.ylabel("mse")
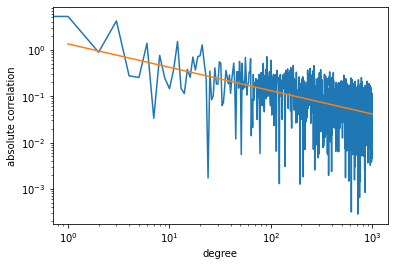
plt.show()
To understand why we are seeing a double descent curve for Legendre
polynomials, we compute the correlation between features
and response
:
cor = []
for i in range(F.shape[1]):
cor.append(np.abs(np.correlate(F[:,i], y)))A plot of the result shows that the correlation decreases exponentially,
whereby we are essentially adding noise to the feature matrix
.
cor_x = np.log(list(range(1, len(cor)+1)))
cor_x = np.array(cor_x).reshape(-1, 1)
cor_y = np.log(cor)
cor_z = np.linspace(1, len(cor), 100).reshape(-1, 1)
clf = LinearRegression()
clf.fit(cor_x, cor_y)
plt.plot(cor)
plt.plot(cor_z, np.exp(clf.predict(np.log(cor_z))))
plt.xscale('log')
plt.xlabel('degree')
plt.yscale('log')
plt.ylabel('absolute correlation')
plt.show()