A Jupyter notebook with the Keras model that we used to predict water point functionality from an image. The images we used are not publicly available but you can run the same experiments against the Kaggle Cats vs. Dogs dataset. The image preparation code that we've used is available in this fork of gigasquid's kagge-cats-dogs repository.
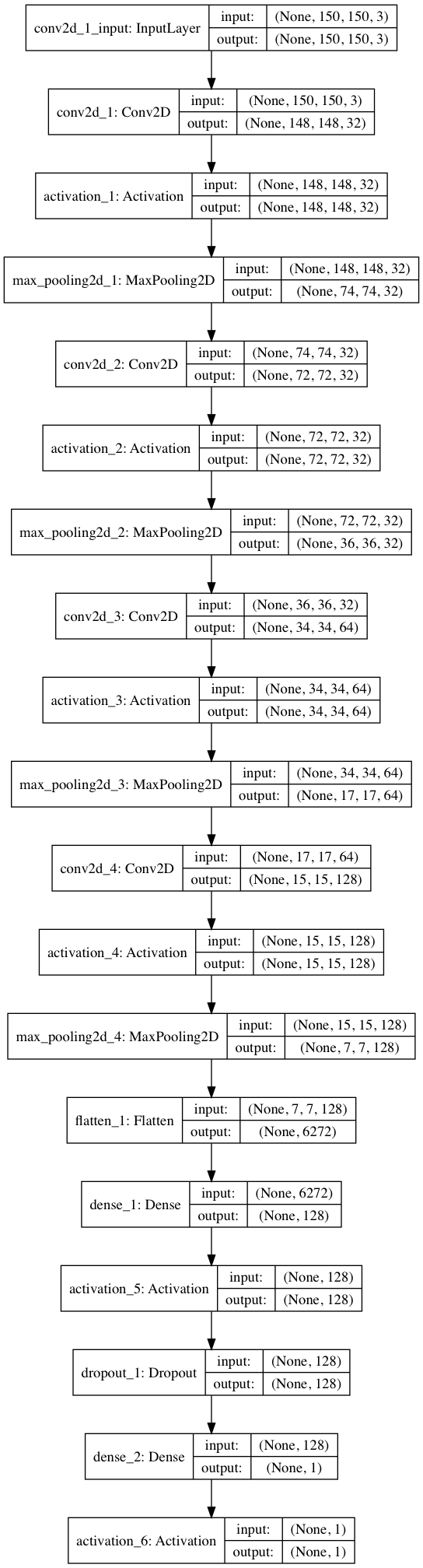
Default model is a feed forward neural network with four 2D convolutional layers of 32, 32, 64, and 128 nodes, all using a rectified linear unit activation function and a 2 by 2 pool size. This is followed by a fully connected layer of 128 nodes and a dropout layer to prevent overfitting. Finally, we use a sigmoid activation function to model the single class binary output of functioning or not-functioning.
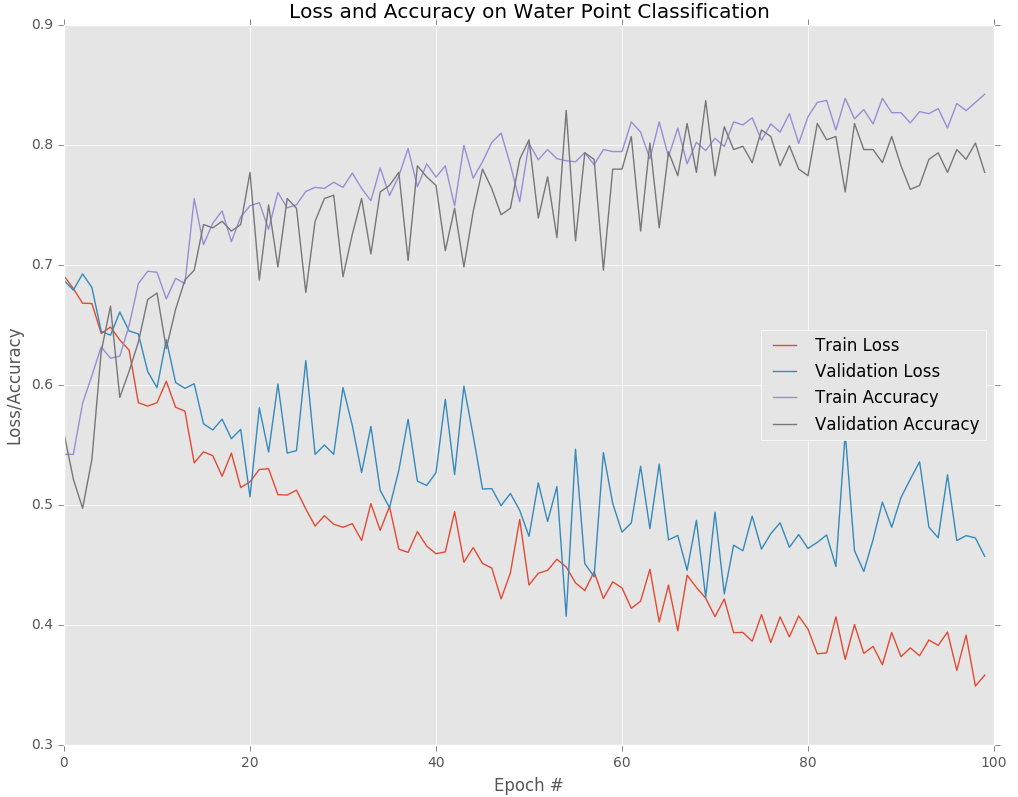
On our dataset the above model obtains 77.7% validation accuracy after 100 epochs:
Samples images and neural network activations:
There are also a number of improvements to the model that we can experiment with. The current hyper-parameters were chosen with a coarse grid search, we should do a fine grid search over the hyper-parameters and add additional hyper-parameters to the search space, including pool size and optimizer. We should experiment with additional network architectures, both deeper and wider. Although preliminary tests did not produce good results, we should also experiment further with transfer learning using pre-existing network weights, such as ImageNet.
- Duchi, Hazan, and Singer, Adaptive Subgradient Methods for Online Learning and Stochastic Optimization
- Guss and Salakhutdinov, On Characterizing the Capacity of Neural Networks using Algebraic Topology
- Kingma and Ba, Adam: A Method for Stochastic Optimization