脱関数化を実用する 2
私たちは、リストと木に対する規範的な (canonical) 高階のプログラムをいくつか考え、それらを脱関数化する。それぞれの場合について、脱関数化は知られているものの関係のない解を生み出す。そのあと私たちは、データ構造の高階な表現を与えるチャーチ符号化を使う。チャーチ符号されたデータ構造を脱関数化した結果について考え、その脱関数化した結果をチャーチ符号化した結果について考える。
二分木を葉 (leaf) のリストへと平坦化するために、葉をカリー化されたリスト構成子に、そして節点 (node) を関数合成に、準同型的に (homomorphically) マップするという方法を選ぶ。つまりリストを、リストからリストへの関数からなるモノイドへとマップするのだ。この定義は関数合成に元々備わっている結合性に依存している。
data BT a = Leaf a
| Node (Bt a) (Bt a)
cons :: a -> [a] -> [a]
cons x xs = x : xs
flatten :: BT a -> [a]
flatten t = walk t []
where
walk :: BT a -> [a] -> [a]
walk (Leaf x) = cons x
walk (Node t1 t2) = walk t1 . walk t2walkの結果をイータ展開し、consと.をインライン化することで、蓄積引数付きの高速な平坦化関数のカリー化されたバージョンが得られる。
flatten_ee :: BT a -> [a]
flatten_ee t = walk t []
where
walk :: BT a -> [a] -> [a]
walk (Leaf x) a = x : a
walk (Node t1 t2) a = walk t1 (walk t2 a)flatenを脱関数化するのも有益である。2つの関数の値（一方は葉に対するもの、一方は節点に対するもの）が生まれるので、それらは2つの構成子を持つデータ型を生み出す。flattenは準同型であるので、新しいデータ型は二分木のデータ型と同型であり、それゆえに関連する適用関数は森林伐採 (deforestation) を使う [[53](脱関数化を実用する 8#reference53)] などして入力の木に直接作用するようにすることもできる。いずれにせよ、私たちはこの適用関数を蓄積引数付きの高速な平坦化関数の脱カリー化されたバージョンとして認識する。
data Lam a = Lam1 a
| Lam2 (Lam a) (Lam a)
apply :: (Lam a, [a]) -> [a]
apply (Lam1 x, xs) = x : xs
apply (Lam2 f1 f2, xs) = apply (f1, apply (f2, xs))
cons_def :: a -> Lam a
cons_def x = Lam1 x
o_def :: (Lam a, Lam a) -> Lam a
o_def (f1, f2) = Lam2 f1 f2
flatten_def :: BT a -> [a]
flatten_def t = apply (walk t, [])
where
walk :: BT a -> Lam a
walk (Leaf x) = cons_def x
walk (Node t1 t2) = o_def (walk t1, walk t2)リストからリストへの関数のモノイドは、ヒューズの新奇なリストの表現 [[28](脱関数化を実用する 8#reference28)] に対応している。次はこれを扱って行く。
1980年代半ば、ヒューズは中間リストを部分的に適用された連結関数 (concatenation functions) として表現することを提案した [28]。この手法では、リストxsを構成する代わりに関数抽象\ ys -> xs ++ ysを実体化する。高階表現の重要な性質は、リストは定数時間で連結されうるということである。ゆえに、以下の愚直なバージョンのreverseは、リストが線型時間で連結される連結リストの通常の表現でのような二次時間 (quadratic time) ではなく、線型時間で動作する。
append :: [a] -> [a] -> [a]
append xs ys = xs ++ ys
reverse :: [a] -> [a]
reverse xs = walk xs []
where
walk [] = append []
walk (x : xs) = walk xs . append [x]このプログラムを脱関数化しよう。まずヒューズと同様に、私たちは空リストを付け加えることは恒等関数であり、一つの要素を付け加えることは結局はその要素をコンスすることである、ということを認識しよう。
id :: [a] -> [a]
id ys = ys
cons :: a -> [a] -> [a]
cons x xs = x : xs
reverse :: [a] -> [a]
reverse xs = walk xs []
where
walk [] = id
walk (x : xs) = walk xs . cons x関数空間[a] -> [a]は3つの関数の値（一方の条件分岐におけるid、そしてもう一方における、要素をコンスした結果とwalkを呼び出した結果）のせいで生まれる。
ゆえに私たちは3つの構成子を持つデータ型と関連する適用関数を使ってプログラムを脱関数化する。
data Lam a = Lam0
| Lam1 a
| Lam2 (Lam a) (Lam a)
apply :: (Lam a, [a]) -> [a]
apply (Lam0, ys) = ys
apply (Lam1 x, ys) = x : ys
apply (Lam2 f g, ys) = apply (f, apply (g, ys))このデータ型は、ヒューズの中間リストのモノイドにおいて、連結が（ここではLam2について）定数時間で実行されるということを分かりやすく示している。
脱関数化されたプログラムの残りの部分は以下の通りである。
id_def :: Lam a
id_def = Lam0
cons_def :: a -> Lam a
cons_def x = Lam1 x
o_def :: (Lam a, Lam a) -> Lam a
o_def (f, g) = Lam2 f g
reverse_def xs = apply (walk xs, [])
where
walk [] = id_def
walk (x : xs) = o_def (walk xs, cons_def x)補助関数はデータ構成子の別名でしかない。Lam1とLam2がいつも互いに関連して使われているということも見て取れる。ゆえに、両者は単一の構成子Lam3へと融合できるし、両者の処置もapply_lamへと融合できる。そうして得られるのが次のものである。
data Lam_alt a = Lam0
| Lam3 (Lam_alt a) a
apply_lam_alt :: (Lam_alt a, [a]) -> [a]
apply_lam_alt (Lam0, ys) = ys
apply_lam_alt (Lam3 f x, ys) = apply_lam_alt (f, x : ys)
reverse_def_alt :: [a] -> [a]
reverse_def_alt xs = apply_lam_alt (walk xs, [])
where
walk :: [a] -> Lam_alt a
walk [] = Lam0
walk (x : xs) = Lam3 (walk xs) x[§2.1](脱関数化を実用する 2#section2-1) と同様、reverse_def_altが入力のリストをデータ型lam_altへと準同型的に埋め込むということが分かる。ゆえに関連する適用関数は入力のリストに直接働くようにすることができる。また、私たちはapply_lam_altを蓄積引数のある高速な反転関数の脱カリー化されたバージョンとして認識する。
ヒューズは、文字列から単語を取り出す「フィールズ (fields)」関数を定義するためにも、中間リストの彼独自の表現を使った。彼の表現はフィールズ関数の効率的な実装を生み出す。実際、上述の反転関数については、この実装を脱関数化すると単語を逆順に蓄積していき、すべての単語が見つかったら高速な反転関数を使う、という高速に動作する実装を与える。ゆえに脱関数化はヒューズの表現の効率性を確証付けるのである。
値をチャーチ符号化するということは、要は、その値に対する演算が、その値の表現を特定のラムダ項に適用することでなされるような方法で、その値をラムダ項によって表現することである [[3](脱関数化を実用する 8#reference3),[9](脱関数化を実用する 8#reference9),[24](脱関数化を実用する 8#reference24),[33](脱関数化を実用する 8#reference33)]。
データ構造は始域 (domain) における和である。（データ構造が帰納的ならば、始域は再帰的である。）和は対応する入射関数 (injection function) とケースディスパッチによって定義される [[56](脱関数化を実用する 8#reference56), page 133]。データ構造のチャーチ符号化は、(1) 入射関数とケースディスパッチをラムダ項と組み合わせ (2) 関数適用により操作する、ということにある。
このセクションのこれ以降では、簡潔さのために、脱カリー化されている、チャーチ符号化されたデータ構造しか考えない。こうすることで、私たちは全体を脱関数化できるのである。
例えば、単一型の［1番目の型と2番目の型が同じである］チャーチ式ペア (monotyped Church pair) とその選択関数は以下のように定義される。
church_pair :: (a, a) -> ((a, a) -> a) -> a
church_pair (x1, x2) = \s -> s (x1, x2)
church_fst :: (((a, a) -> a) -> b) -> b
church_fst p = p (\(x1, x2) -> x1)
church_snd :: (((a, a) -> a) -> b) -> b
church_snd p = p (\(x1, x2) -> x2)ペアは1引数を期待するラムダ項として表現されている。この引数は、1番目か2番目への射影 (projection) に対応する選択関数である。
一般に、データ構造を定義する入射関数は以下の形である。
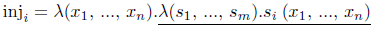
では、チャーチ符号化されたデータ構造を脱関数化したら、つまり入射関数の結果を脱関数化したらどうなるだろうか？それぞれの入射関数は、引数が上で下線を引いた項の自由変数に対応しているような、データ構成子を生み出す。これらの自由変数は正確に入射関数の引数であり、これらの引数はそれ自体チャーチ符号化された元々の構成子の引数である。
したがって、チャーチ符号化されたデータ構造を（つまり、入射関数の結果を）脱関数化することで、チャーチ符号化の前と同じデータ構造が生まれる。これらのデータ構造は、脱関数化によって導入された補助の適用関数を通して、アクセスされる。
例えば、単一型のチャーチ式ペアとその選択関数は、以下のように脱関数化される。
- 選択関数は閉じた項であるので、対応する構成子は引数が無い。定義により、選択関数は引数のタプルを渡されてそのうちの一つを返す。
data Sel = Fst | Snd
apply_sel :: (Sel, (a, a)) -> a
apply_sel (Fst, (x1, x2)) = x1
apply_sel (Snd, (x1, x2)) = x2- ペアへの入射関数が1つあり、それゆえにその関数は、
Church_pairの結果の2つの自由変数の値のための1つの構成子を持つデータ型を生み出す。対応する適用関数は選択を行う。（注意：apply_pairはChurch_pairのカリー化された型を反映しながらapply_selを呼び出す。）
data Pair a = Pair a a
apply_pair :: (Pair a, Sel) -> a
apply_pair (Pair x1 x2, s) = apply_sel (s, (x1, x2))- 最後に、ペアを構成するということは、要はタルスキの方法で [[21](脱関数化を実用する 8#reference21)] ペアを構成することだと言える。また、ペアの構成要素を選択するには
apply_pairを呼び出せばよい（この関数自体はapply_selを呼び出している）。
church_pair_def :: (a, a) -> Pair a
church_pair_def (x1, x2) = Pair x1 x2
church_fst_def :: Pair a -> a
church_fst_def p = apply_pair (p, Fst)
church_snd_def :: Pair a -> a
church_snd_def p = apply_pair (p, Snd)最適化を行うコンパイラならばどちらの適用関数もインライン化するだろう。結果として生まれる選択関数は、脱関数化されたペアの構成子とともに、チャーチ符号化以前の元々のペアの定義と一致しているだろう。
チャーチ符号化された二分木についてちょっと考えてみよう。2つの入射関数が生まれる：ひとつは葉に対するもの、ひとつは節点に対するものである。チャーチ符号化された木は2つの引数を期待しているラムダ項である。これらの引数は木が葉である場合と木が節点である場合にそれぞれ対応している選択関数である。
church_leaf x = \(s1, s2) -> s1 x
church_node (t1, t2) = \(s1, s2) -> s2 (t1 (s1, s2), t2 (s1, s2))二分木の帰納的な性質により、church_nodeは選択関数を部分木へと伝える。
一般に、データ構造を定義する入射関数のそれぞれは以下の形をしている。
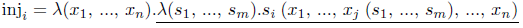
ここで、xj (s1, ..., sm) はデータ型の中にある各 xj について生まれる。
では、チャーチ符号化された再帰的データ構造（つまり入射関数の結果）を脱関数化したらどうなるのだろうか？またしても、それぞれの入射関数は、引数が上で下線を引いた項の自由変数に対応しているような、データ型の構成子を生み出す。これらの自由変数は正確に入射関数の引数であり、その引数自体がチャーチ符号化された元々の構成子の引数である。
ゆえに、脱関数化されたチャーチ符号化された再帰的データ構造（つまり入射関数の結果）を脱関数化しても、チャーチ符号化以前と同じデータ構造が得られるのである。これらのデータ構造は、脱関数化によって導入された補助の適用関数を通してアクセスされる。
ではチャーチ符号化された二分木に戻ろう。脱関数化はプログラム全体の変換であるので、私たちはプログラム全体について考える。ここではチャーチ符号化された二分木の深さを計算する関数を考えよう。この関数は引数に2つの選択肢を渡す。1番目は0を常に返す定数関数であり、葉の深さを説明している。2番目は各節点の部分木の深さに適用される関数であり、2つの部分木の深さの最大値を取って1を足すことで節点の深さを計算する。
church_depth t = t (\x -> 0, \(d1, d2) -> max d1 d2 + 1)このプログラムの全体は以下のように脱関数化される。
- 選択肢は2つの構成子
Sel_LeafとSel_Node、そして対応する2つの適用関数apply_sel_leafとapply_sel_nodeを生む。
data Sel_Leaf = Sel_Leaf
apply_sel_leaf (Sel_Leaf, x) = 0
data Sel_Node = Sel_Node
apply_sel_node (Sel_Node, (d1, d2)) = max d1 d2 + 1- 入射関数については、上述のように、2つの構成子
LeafとNode、そして対応する適用関数を生み出す。
data Tree a = Leaf a
| Node (Tree a) (Tree a)
church_leaf_def x = Leaf x
church_node_def (t1, t2) = Node t1 t2- 最後に、脱関数化されたメイン関数は得た引数を2つの変換子に適用する。
depth_def :: Tree a -> Int
depth_def t = apply_tree (t, (Sel_Leaf, Sel_Node))
apply_tree :: (Tree a, (Sel_Leaf , Sel_Node)) -> Int
apply_tree (Leaf x, (sel_leaf, sel_node)) = apply_sel_leaf (sel_leaf, x)
apply_tree (Node t1 t2, (sel_leaf, sel_node)) =
apply_sel_node (sel_node, (apply_tree (t1, (sel_leaf, sel_node)),
apply_tree (t2, (sel_leaf, sel_node))))またしても、最適化を行うコンパイラならば両方の適用関数をインライン化し、Sel_LeafとSel_Nodeは無くなるだろう。結果生まれるものは、チャーチ符号化以前の元々の二分木の定義と一致している。
上でチャーチ式ペアとチャーチ式木について簡単に実証できるように、チャーチ符号化されたデータ構造を脱関数化した結果をチャーチ符号化すると、チャーチ符号化されたデータ構造が戻ってくる。適用関数は単純な適用に戻り、主役のデータ構造の構成子は入射関数となり、補助のデータ構造の構成子は選択関数となる。
しかし実用上は、選択関数が一度しか現れない場合、チャーチ符号化の間において選択関数をインライン化することが多い。シヴァーズはこれを「超 ベータ (super-beta)」と呼んでいる [[46](脱関数化を実用する 8#reference46)]。こうすることで、[§4.1.3](脱関数化を実用する 4#section4-1-3) と [§4.2.3](脱関数化を実用する 4#section4-2-3) で説明しているように、脱関数化の本当の逆が得られる。この「再関数化」も、ダンヴィー・グロバオアー・ライガーの目標指向の (goal-directed) 評価についての研究 [[13](脱関数化を実用する 8#reference13)] などにおいて、使われている。
チャーチ符号化されたデータ構造において、選択関数は継続の香りをしている。[§3](脱関数化を実用する 3#section3) において、私たちは継続をどのように脱関数化するのかについて考える。
私たちは多種多様な典型的高階のプログラムについて考え、それらを脱関数化した。結果として得られるプログラムは、関数型プログラミングにおける高階性の効果を明らかにする一階の見方を提供している。例えば、型a -> bの関数を返す場合、しばしばこの関数をaの型を持つ蓄積引数を持つように書く方法が自然に得られる。別の例において、脱カリー化されたチャーチ符号化されたデータ構造を脱関数化することにより、チャーチ符号化以前に戻ったデータ構造が得られる。これは、チャーチ符号化がデータの流れを制御の流れに変換し、脱関数化がその逆を行うということを示している。