Function definitions derived from graph declarations.
ALPHA RELEASE
I was at Strange Loop 2012 in Saint Louis, where the Prismatic team did a talk about their Graph library for building up complex processes in a declarative style. At the time, Prismatic had not yet released Graph as open-source. I wanted something like it, so I wrote my own.
I also wanted to do something new with the dependency graph library I wrote for tools.namespace 0.2.0. Flow turned out to be pretty easy given a data structure to represent a DAG.
Flow is on Clojars
Latest release is 0.1.0
Leiningen dependency information:
[com.stuartsierra/flow "0.1.0"]
The Git master branch is at version 0.1.1-SNAPSHOT.
Flow is a small library for building up functions as discrete
steps without specifying the order of those steps. This can help
clarify functions that have lots of let-bindings. For example, this
function:
(defn process [alpha beta]
(let [gamma (subprocess-a alpha beta)
delta (subprocess-b alpha gamma)
epsilon (subprocess-c gamma delta)]
(subprocess-d gamma delta epsilon)))
Could be written as a Flow like this:
(require [com.stuartsierra.flow :as flow])
(def process-flow
(flow/flow
:result ([gamma delta epsilon]
(subprocess-d gamma delta epsilon))
:gamma ([alpha beta] (subprocess-a alpha beta))
:delta ([alpha gamma] (subprocess-b alpha gamma))
:epsilon ([gamma delta] (subprocess-c gamma delta))))
The body of a Flow consists of pairs of an output and a fntail.
The fntail is a list with an argument vector and body just like
fn.
The output is a symbol binding for the return value the that function.
Symbols that appear as both outputs and arguments to fntails create
dependency relationships. In the example above, the result output
depends on gamma, delta, and epsilon.
Symbols which appear in argument vectors but not as output-symbols are
the /inputs/ to the flow. In the example above, alpha and beta are
inputs.
The order of the pairs doesn't matter: you can use a symbol in an argument vector before it is declared as an output.
For demonstration, I'll defined the subprocesses to be addition:
(def subprocess-a +)
(def subprocess-b +)
(def subprocess-c +)
(def subprocess-d +)
Once you have defined a Flow, you can execute it by providing a map of inputs. You get back a map containing the final result plus all the intermediate outputs computed along the way.
(flow/run process-flow {:alpha 1 :beta 2} [:result])
;;=> {:result 14, :epsilon 7, :delta 4, :gamma 3,
;; :alpha 1, :beta 2}
You can also specify which outputs you want. The Flow only computes as much as it has to:
(flow/run process-flow {:alpha 1 :beta 2} [:gamma :delta])
;;=> {:delta 4, :gamma 3, :alpha 1, :beta 2}
You can also override some or all of the outputs by providing them as input:
(flow/run process-flow {:alpha 1 :beta 2 :gamma 30} [:result])
;;=> {:result 122, :epsilon 61, :delta 31, :alpha 1,
;; :beta 2, :gamma 30}
If you know the input keys in advance, you can precompile a Flow into a function which will run faster. Call the function with a map of inputs, and you get a map of all the outputs:
(def compute (flow/compile process-flow [:alpha :beta]))
(compute {:alpha 1 :beta 2})
;;=> {:result 14, :epsilon 7, :delta 4, :gamma 3,
;; :alpha 1, :beta 2}
As with run, you can optionally specify which outputs you want:
(def compute-gamma
(flow/compile process-flow [:alpha :beta] [:gamma]))
(compute-gamma {:alpha 1 :beta 2})
;;=> {:gamma 3, :alpha 1, :beta 2}
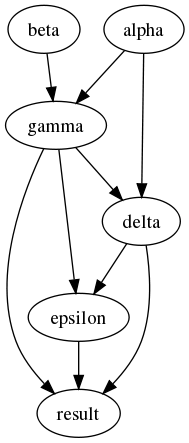
If you have the Graphviz program installed, you can generate
visualizations of a flow. The dot function prints out a
Graphviz-compatible representation of the flow:
(flow/dot process-flow)
;; digraph "flow" {
;; "alpha" -> "delta" ;
;; "alpha" -> "gamma" ;
;; "epsilon" -> "result" ;
;; "delta" -> "epsilon" ;
;; "delta" -> "result" ;
;; "beta" -> "gamma" ;
;; "gamma" -> "epsilon" ;
;; "gamma" -> "result" ;
;; "gamma" -> "delta" ;
;; }
Write that out to a file:
(flow/write-dotfile process-flow "flow.dot")
Then run Graphviz:
$ dot -Tpng -o flow.png flow.dot
And see the results:
A Flow is just a map whose values are functions. You can construct
this map youself or assoc new functions into an existing Flow.
Each function must take a single argument: the map of inputs and
accumulated results. The function returns a value to be assoc'd into
the results map. Each function must also have metadata which describes
the result keys it depends on; if this metadata is missing it means
the function doesn't depend on anything. The with-inputs function
will add this metadata to any function:
(def process-flow-2
(assoc process-flow
:epsilon (flow/with-inputs [:alpha :beta]
(fn [{:keys [alpha beta]}]
(+ (* 100 alpha) beta)))))
(flow/run process-flow-2 {:alpha 1 :beta 2})
;;=> {:result 109, :epsilon 102, :delta 4,
;; :gamma 3, :alpha 1, :beta 2}
The flow-fn macro is a syntactic helper to create a function with
the necessary metadata and destructure the input map. The previous
example could be written:
(def process-flow-2
(assoc process-flow
:epsilon (flow/flow-fn [alpha beta]
(+ (* 100 alpha) beta))))
Small, self-contained Flows can be expressed as flow-let, which
expands to a series of ordinary let bindings:
(flow/flow-let
[alpha ([] 1)
beta ([] 2)
result ([gamma delta epsilon]
(subprocess-d gamma delta epsilon))
gamma ([alpha beta] (subprocess-a alpha beta))
delta ([alpha gamma] (subprocess-b alpha gamma))
epsilon ([gamma delta] (subprocess-c gamma delta))]
(str "The result is " result))
;;=> "The result is 14"
- Release 0.1.0 on 14-Dec-2012
- Complete rewrite
- All breaking changes
- Flows are normal maps
- Release 0.0.1 on 12-Oct-2012
Copyright (c) 2012 Stuart Sierra. All rights reserved. This program and the accompanying materials are made available under the terms of the Eclipse Public License v1.0 which accompanies this distribution, and is available at http://www.eclipse.org/legal/epl-v10.html