SymPy vs. Matlab
 vs.
vs. 
SymPy and Symbolic Math Toolbox are Computer algebra systems.
- Computer Algebra System
-
A software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.
Sympy is a Python library for symbolic computation that aims to become a full-featured computer algebra system and to keep the code simple to promote extensibility and comprehensibility.
SymPy was started by Ondřej Čertík in 2005 and he wrote some code in 2006 as well. In 11 March 2007, SymPy was realeased to the public. The latest stable release of SymPy is 0.7.1 (29 July 2011). As of beginning of December 2001 there have been over 150 people who contributed at least one commit to SymPy.
SymPy can be used:
- Inside Python, as a library.
- As an interactive command line, using IPython.
SymPy is entirely written in Python and does not require any external libraries, but various programs that can extend its capabilities can be installed:
- gmpy, Cython --> speed improvement.
- Pyglet, Matplotlib --> 2d and 3d plotting.
- IPython --> interactive sessions.
SymPy is available online at SymPy Live. The site was developed specifically for SymPy. It is a simple web shell that looks similar to iSymPy under the standard Python interpreter. SymPy Live uses Google App Engine as computational backend.
Symbolic Math Toolbox™ software lets you to perform symbolic computations within the MATLAB® numeric environment. It provides tools for solving and manipulating symbolic math expressions and performing variable-precision arithmetic. The toolbox contains hundreds of symbolic functions that leverage the MuPAD® engine for a broad range of mathematical tasks
Symbolic Math Toolbox software also includes the MuPAD language, which is optimized for handling and operating on symbolic math expressions. In addition to covering common mathematical tasks, the libraries of MuPAD functions cover specialized areas such as number theory and combinatorics.
Originally developed by the MuPAD research group at the University of Paderborn, Germany, development was taken over by the company SciFace Software GmbH & Co. KG in cooperation with the MuPAD research group and partners from some other universities starting in 1997. Former versions of MuPAD Pro were bundled with SciLab. Its version 14 release was adopted as the CAS engine for the MathCAD software package. In September 2008, SciFace was purchased by MathWorks and the MuPAD code was included in the Symbolic Math Toolbox add-on for MATLAB. On 28 September 2008, MuPAD was withdrawn from the market as a software product in its own right.However, it is still available in the Symbolic Math Toolbox in MATLAB and can also be used as a stand-alone program.
There are two toolboxes: • The basic Symbolic Math Toolbox is a collection of more than 100 MATLAB functions that provide access to the Maple kernel using a syntax and style that is a natural extension of the MATLAB language. The basic toolbox also allows you to access functions in the Maple linear algebra package. • The Extended Symbolic Math Toolbox augments this functionality to include access to all nongraphics Maple packages, Maple programming features, and user-defined procedures. With both toolboxes, you can write your own M-files to access Maple functions and the Maple workspace
Symbolic Math Toolbox is a paid software, but a trial can be downloaded from the Matlab website.
| System | Windows | Mac OS X | Linux | BSD | Solaris |
|
|
|
|
|
Yes |
|
|
|
|
|
|
No |
|
Declaration of symbolic variables
Symbolic Math Toolbox :: >> a = sym('a1')
Sympy :: >> a = Symbol('a1')
In SymPy, to raise something to a power, you must use **, not ^. However, in Symbolic Math Toolbox, both ^ and ** mean exponentiation.
Limits
Sympy
Example1 :: >>> from sympy import * >>> x=Symbol('x') >>> limit (sin(x)/x,x,0) 1
Example2 :: >>> from sympy import * >>> x=Symbol('x') >>> h=Symbol('h') >>> limit((sin(x + h) - sin(x))/h, h, 0) cos(x)
Symbolic Math Toolbox
syntax limit(expr,x,a) limit(expr,a) limit(expr) limit(expr,x,a,'left') limit(expr,x,a,'right')
Example 1 :: syms x h; limit(sin(x)/x)
ans =1
Example 2 :: limit((sin(x + h) - sin(x))/h, h, 0)
ans =cos(x)
differentiation
Symbolic Math Toolbox :: >> syms x >> f = x^2 - 3*x + 4; >> diff(f) % or diff('x^2 - 3*x + 4') ans = 2*x - 3
Differentiation of Multivariable Functions :: >> syms a b >> f = [a^2 + b^2 - 1, a + b - 1]; >> Jac = jacobian(f) Jac = [ 2*a, 2*b] [ 1, 1]
SymPy
Examples :: >>> diff(cos(x*3), x) -3X*2sin(X*3) >>> diff(tan(x),x) tan(X)2 + 1 >>> diff(x2+x,x) 2X + 1
Polynomial Algebra
Reduced Gröbner bases computation
SymPy
To compute a reduced Gröbner basis for a set of polynomials use groebner() function. The function accepts various monomial orderings, e.g.: lex, grlex and grevlex, or a user defined. :: >>> s=Symbol('s') >>> f = expand((1 - c*2)5 (1 - s*2)5 (c*2 + s2)10) >>> groebner([f, c2 + s2 - 1]) [c2 + s2 - 1, c20 - 5c*18 + 10c*16 - 10c*14 + 5c*12 - c*10]
Symbolic Math Toolbox
groebner::gbasis(polys) computes a reduced Gröbner basis of the ideal generated by the polynomials in the list polys. call ::groebner::gbasis(polys, <order>, <Options>) :: groebner::gbasis([x^2 - y^2, x^2 + y], LexOrder) [x^2 + y, x^4 - y^4]
Consider the following nonlinear differential equation: :: Ly := x^2*diff(y(x),x)+y(x)-x
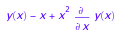
We compute the series solutions at the point which is a singular point: :: ode::series(Ly, y(x), x=0) .. image:: 12.png
Then we compute the series solutions at the regular point : :: ode::series(Ly, y(x), x=1) .. image:: 13.png
And we can also put some initial conditions at the point : :: ode::series({y(1)=1, Ly}, y(x), x=1) .. image:: 14.png
SymPy :: >>> f(x).diff(x, x) + f(x)
2
d
- f(x) + ---(f(x))
2
dx
- >>> dsolve(f(x).diff(x, x) + f(x), f(x))
f(x) = C1·sin(x) + C2·cos(x)
Series
Symbolic Math Toolbox :: syms x f = 1/(5 + 4*cos(x)); T = taylor(f, 8) 6 4 2 49 x 5 x 2 x ------ + ---- + ---- + 1/9 131220 1458 81
Sympy :: >>>: from sympy import *
>>>: x = Symbol('x')
>>>: cos(x).series(x, 0, 14) >>>: 2 4 6 8 10 12 x x x x x x ⎛ 14⎞ 1 - ── + ── - ─── + ───── - ─────── + ───────── + O⎝x ⎠ 2 24 720 40320 3628800 479001600
>>>: (1/cos(x**2)).series(x, 0, 14) >>>: 4 8 12 x 5⋅x 61⋅x ⎛ 14⎞ 1 + ── + ──── + ────── + O⎝x ⎠ 2 24 720
Matrix
SymPy
Defining a Matrix
- ::
-
- >>> Matrix(2,-1,0],[-1,2,-1],[0,-1,2)
-
[ 2, -1, 0] [-1, 2, -1] [ 0, -1, 2]
Inverse of a Matrix :: >>> M=Matrix(2,-1,0],[-1,2,-1],[0,-1,2) >>> M.inv() [3/4, 1/2, 1/4] [1/2, 1, 1/2] [1/4, 1/2, 3/4]
Determinant of a matrix :: >>> M.det() 4
Symbolic Math Toolbox
Defining a Matrix :: >> M=[2 -1 0;-1 2 -1;0,-1,2]
M =
2 -1 0
- -1 2 -1
0 -1 2
Determinant of a Matrix :: >> det(M)
ans = 4
SymPy aims to be a lightweight normal Python module so as to become a nice open source alternative to Symbolic Math toolbox. Its goal is to be reasonably fast, easily extended with your own ideas, be callable from Python and could be used in real world problems. Another advantage of SymPy compared to Symbolic Math Toolbox is that since it is written in pure Python (and doesn't need anything else), it is perfectly multiplatform, it's small and easy to install and use.
You can choose to use either SymPy or Symbolic Math toolbox, depending on what your needs are.